• Decision Making and Reinforcement Learning
  • Markov Decision Processes
  • MDPs: More About Rewards 
  • sequences of Rewards: Assumptions
  • Policies
  • The Bellman Equation
  • Recap

哎呀呀，上这个课被虐了呀。看别的课程都1.5倍速，看这个视频还不到0.5倍速。

Decision Making and Reinforcement Learning

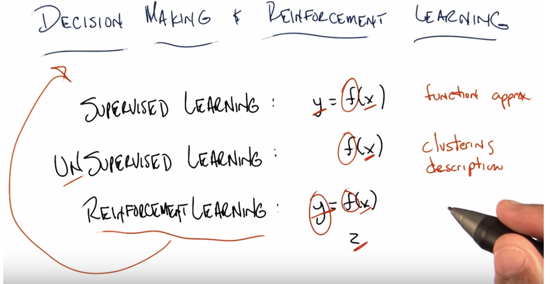
Supervised Learning: y = f(x), given many x, y pairs, determine function f to determine the relationship between x and y.

Unsupervised Learning: f(x), given a lot of x, determine function f to cluster or describe x.

Reinforcement Learning: y = f(x) with z, given x and z, determine function f which can generate y.

RL is one of the ways to perform decision making.

Markov Decision Processes

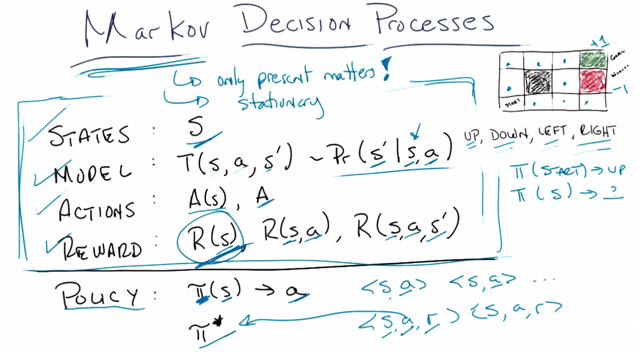
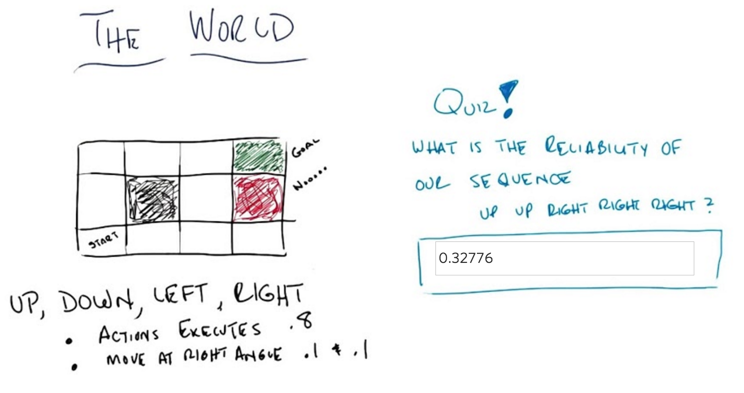
States: set of tokens which describe every state that one could be in,  

Model/Transition Function: probability that you’ll end up transition to s’ given you are in state s and taking action a. This is ‘physics’ or rules of the world(not changeable) . 

Action: A(s), things you can do in a given state, a function of state, rule you can play; or A, a set actions not depends regardless of state.

Reward: scalar value that you get for being in a state. Usefulness of entering a state/and taking an action/and ending up into s’ 

S, T, A and R define the problem, policy is the solution,

Policy: the solution, a function that takes up a state and tells an action that you’ll take <s,a> while a is the correct action you want to take to maximize the reward 

*Optimal policy:  π*, optimized, maximize long term expected reward. (note, from <s,a,r>, you know s, a and then know the r, based on rewards, find π*)

Recall that in Reinforcement Learning: y = f(x) with z, given x and z, determine function f which can generate y. In Markov process, we know s and r, and we need to learn π to determine a. So, s–>x, r–>z, a–>y, π–>f 

Markovian property :

• –> only the present matters; the transition state only depends on the current state 

• –> Transition model is stationary, rules doesn’t change 

MDPs: More About Rewards 

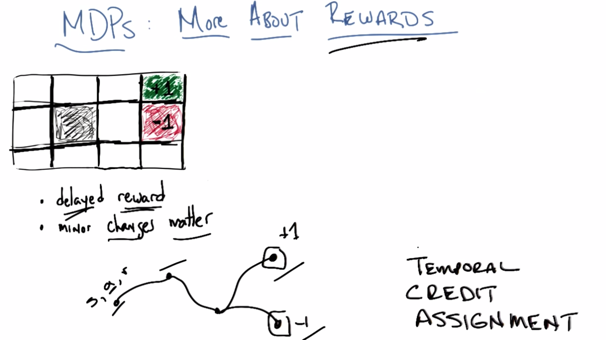
Delayed reward: in each state, we need figure out what action should we take to get the ultimate best rewards at the end.

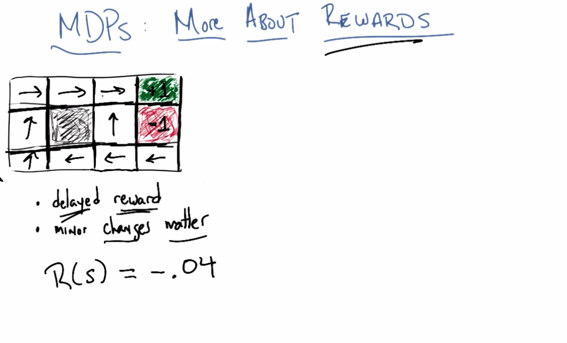
** Minor changes matter: By assigning small negative rewards in each state (except the absorbing state), the learning agent is encouraged to take one of the available actions to leave the current state and pursuit a better outcome.

If R(s) is large positive, it encourages you to stay in the game. If R(s) is large negative (< -1.6294), it encourages you to leave the world ASAP.

Reward is important to define learning behaviour. Rewards depends on domain knowledge. Changing the reward will change the goal of agent.

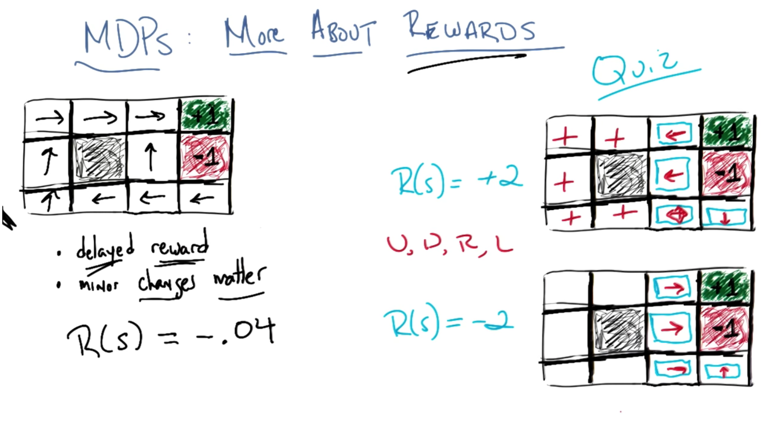
• rationale: when the rewards are positive, the goal becomes never leaving the game. When the rewards are negative, the goal becomes leaving the game ASAP.

sequences of Rewards: Assumptions

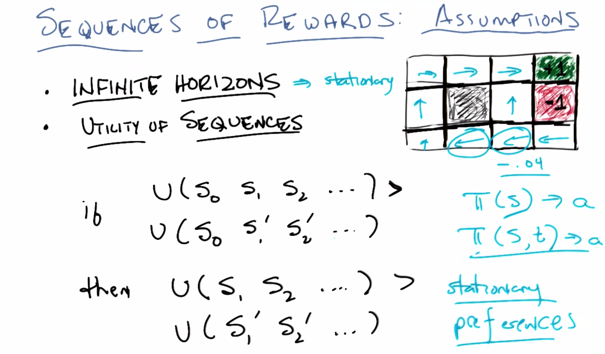
• infinite horizons: if the time step is finite, the policy might change: π(s,t) –> a, and the Markovian property “π is stationary” will not stand anymore. So, we need to assume we have infinite horizons.

• Utility of Sequences: stationary preferences, Utility of all the states is the sum of the rewards of all states.

Since there are infinite number of states, the top sequence and the bottom sequence are essentially the same utility ∞ since the reward are all positive if we use the equation above.

So a new equation is introduced below by introducing a discount factor γ:

The equation introduced Discounted factor of Rewards and made the right side of the equation a geometric series so that the utility of sequences is bounded at Rmax/(1-γ), where 0 ≤ γ <1. This way, the infinite horizons is bounded by a finite number.

Policies

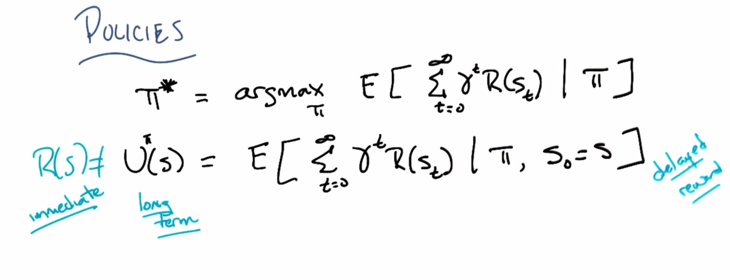
Policy is A mapping from state to action

Optimal policy π*: the policy allow us getting the largest expected discounted rewards when we follow the policy π* .

Utility of a state U(s) is long term expected discounted rewards from this point on; It’s delayed reward.

While Reward is immediate satisfaction.

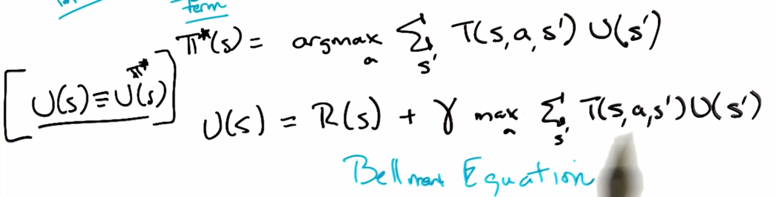
π*(s) is the optimal policy given current state. ** U(s)** is the utility of the state if follow π*. Thus we get the utility of the current state is reward of current state [R(s)] plus the discounted utility from this point on. This is the Bellman Equation.

The Bellman equation has n equations and n unknowns. Because the equations are non-linear (because the max operation), the equations are not easy to solve.

Here list the way to solve the problem: by setting an arbitrary utility and update utility based on neighbours, and repeat until converge. This method is called value iteration. Neighbours are any state that we can reach.

The reason that VI can work is the reward of each state is true and the utility is discounted.

• in this quiz, assuming the initial U of all states but the terminal states is 0. Compute the U at first and second value iteration.

By starting with a guessed policy, the Bellman equation don’t have to do Max when calculating the expected utility. So there are n linear equation with n unknowns, and it’s fairly easy to get the estimation of utility.

The Bellman Equation

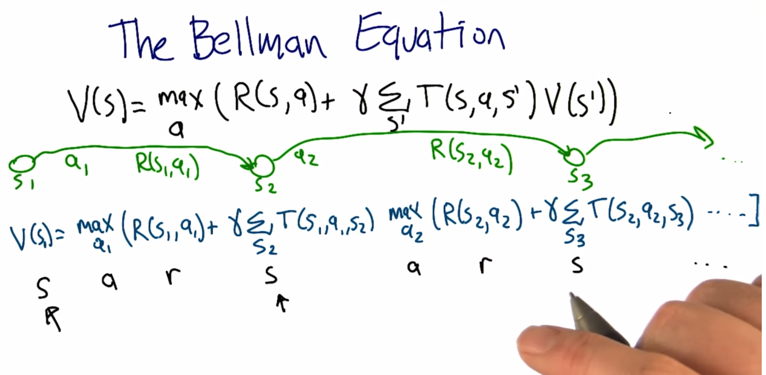
V(s) is infinite sequence with sub V. By regrouping the Value function, we can get Q function as:

and C function as:

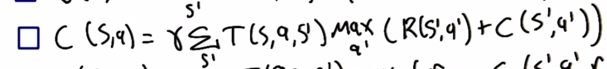
1. In the first equation, we do not know which action a to use to transition into state s ’, so we cannot compute the transition function.
2. Correct answer. In this formula, all the variables are properly defined, and there is a meaningful relationship between the continuation function and the reward function.
3. Notice that there is no meaningful dependency of the max operator on the parameter r (which is already passed in to the continuation function). Also, the variable r ’ is never defined.
4. In this equation, the state s ’’ is not defined, so it does not make sense to pass it into the recursive call of the continuation function.

What’s the difference between V form and Q form and C form of Bellman equation?

1. in value function, V is connected by transition T and reward r. we must know transition and the reward of current state s. V is updated with respect to a state.
2. in quality function, we can rely on experience to update Q, this is useful in reinforcement learning when we do not know T and R ahead of time. Q-value is updated with respect to an action.

We don’t need reward function when we convert Q to C or V. We can convert C to V and q without knowing the transition function.

Recap

2015-08-25 初稿
2015-12-02 revised 好多知识点第n次看才看懂啊……