Intro to Burlap
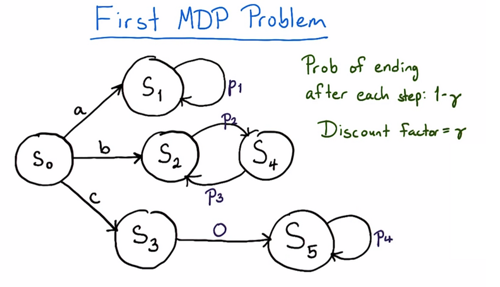
In this introduction lecture to Burlap, I learned how to use BURLAP to setup a MDP.
Steps includes:
- setup domain (using GraphDefinedDomain)
- setup nodes (states)
- setup actions
- initialize state
- setup reward function, termination function, hashFactory
- run Value Iteration
- and get the optimal first action.
See the sample code below and readBurLAP documentation to understand the code.
import burlap.behavior.singleagent.planning.stochastic.valueiteration.ValueIteration;
import burlap.behavior.statehashing.DiscreteStateHashFactory;
import burlap.domain.singleagent.graphdefined.GraphDefinedDomain;
import burlap.oomdp.auxiliary.DomainGenerator;
import burlap.oomdp.auxiliary.common.NullTermination;
import burlap.oomdp.core.*;
import burlap.oomdp.singleagent.GroundedAction;
import burlap.oomdp.singleagent.RewardFunction;
public class FirstMDP {
DomainGenerator dg;
Domain domain;
State initState;
RewardFunction rf;
TerminalFunction tf;
DiscreteStateHashFactory hashFactory;
int numStates;
public FirstMDP(double p1, double p2, double p3, double p4) {
int numStates = 6;
this.dg = new GraphDefinedDomain(numStates);
//actions from initial state 0
((GraphDefinedDomain) this.dg).setTransition(0, 0, 1, 1.);
((GraphDefinedDomain) this.dg).setTransition(0, 1, 2, 1.);
((GraphDefinedDomain) this.dg).setTransition(0, 2, 3, 1.);
//transitions from action "a" outcome state
((GraphDefinedDomain) this.dg).setTransition(1, 0, 1, 1.);
//transitions from action "b" outcome state
((GraphDefinedDomain) this.dg).setTransition(2, 0, 4, 1.);
((GraphDefinedDomain) this.dg).setTransition(4, 0, 2, 1.);
//transitions from action "c" outcome state
((GraphDefinedDomain) this.dg).setTransition(3, 0, 5, 1.);
((GraphDefinedDomain) this.dg).setTransition(5, 0, 5, 1.);
this.domain = this.dg.generateDomain();
this.initState = GraphDefinedDomain.getState(this.domain,0);
this.rf = new FourParamRF(p1,p2,p3,p4);
this.tf = new NullTermination();
this.hashFactory = new DiscreteStateHashFactory();
}
public static class FourParamRF implements RewardFunction {
double p1;
double p2;
double p3;
double p4;
public FourParamRF(double p1, double p2, double p3, double p4) {
this.p1 = p1;
this.p2 = p2;
this.p3 = p3;
this.p4 = p4;
}
@Override
public double reward(State s, GroundedAction a, State sprime) {
int sid = GraphDefinedDomain.getNodeId(s);
double r;
if( sid == 0 || sid == 3 ) { // initial state or c1
r = 0;
}
else if( sid == 1 ) { // a
r = this.p1;
}
else if( sid == 2 ) { // b1
r = this.p2;
}
else if( sid == 4 ) { // b2
r = this.p3;
}
else if( sid == 5 ) { // c2
r = this.p4;
}
else {
throw new RuntimeException("Unknown state: " + sid);
}
return r;
}
}
private ValueIteration computeValue(double gamma) {
double maxDelta = 0.0001;
int maxIterations = 1000;
ValueIteration vi = new ValueIteration(this.domain, this.rf, this.tf, gamma,
this.hashFactory, maxDelta, maxIterations);
vi.planFromState(this.initState);
return vi;
}
public String bestFirstAction(double gamma) {
double V1, V2, V3;
String best;
best = "";
ValueIteration vi = computeValue(gamma);
V1 = vi.value( GraphDefinedDomain.getState(this.domain, 1) );
V2 = vi.value( GraphDefinedDomain.getState(this.domain, 2) );
V3 = vi.value( GraphDefinedDomain.getState(this.domain, 3) );
if (V1 >= V2 && V1 >= V3){
best = "action a";
} else if (V2 >= V3 && V2> V1){
best = "action b";
} else if (V3> V2 && V3 > V1){
best = "action c";
}
return best;
// Return "action a" if a is the best action based on the discount factor given.
// Return "action b" if b is the best action based on the discount factor given.
// Return "action c" if c is the best action based on the discount factor given.
// If there is a tie between actions, give preference to the earlier action in the alphabet:
// e.g., if action a and action c are equally good, return "action a".
}
public static void main(String[] args) {
double p1 = 5.;
double p2 = 6.;
double p3 = 3.;
double p4 = 7.;
FirstMDP mdp = new FirstMDP(p1,p2,p3,p4);
double gamma = 0.6;
System.out.println("Best initial action: " + mdp.bestFirstAction(gamma));
}
}
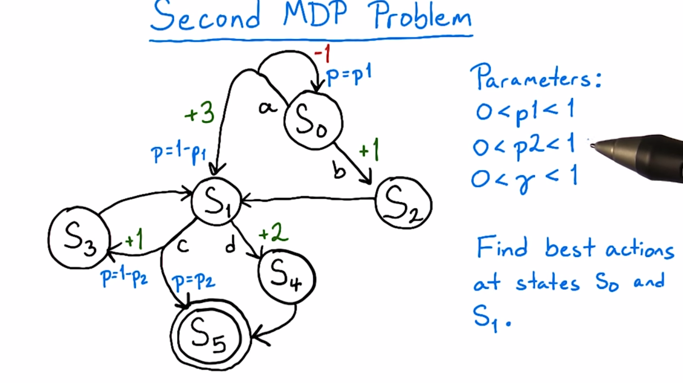
The solution of this second problem will not be posted here since it’s the quiz of the lecture.
2015-08-26 初稿