Reinforcement Learning 第六周课程笔记

Advanced Algorithmic Analysis

1 tells us that VI converges in a reasonable amount of time t* (finite). We know t* exists, but we don’t know when that will happen.
2 Gives us an bound of difference between the policy now and optimal policy. We can take this bound and test when it is a decent time to stop VI and take the current policy.
Both 1 and 2 encourage us choosing a small γ. (γ tells us how further in the future we should look). The effective horizon is H ~ 1/(1-γ).
3 applying Bellman Operator K times to Q functions will shrink the distance between Q functions.

Only one way to solve MDP in polynomile time：solving Bellman equation through Linear Programming. A linear programming problem may be defined as the problem of maximizing or minimizing a linear function subject to linear constraints. ( Defination extracted form this PDF)
Bellman equation has one part that is not linear, the max function. But it can be expressed by a series of linear function and a objective function min.

Primal

in the primal, the objective function is the minimum of sum of all the V_s;
in linear programming, we can change constraints to variables and variables to constraints, and the resulting linear program is equivalent to the old one.

The Dual

Dual is a new linear program comes from the old primal version of linear program (没有推导过程）
q_sa is “Policy flow”, maximize the expected rewards of all states.
For each possible next state, we wanted it to be true that the amount of policy flows going through the next state should be equal to the number of the state it has been visited.

Initialize the first step Q value of all the states to be 0; improve the policy at time t; Apply the policy to calculate the Q value of t+1 step.
Convergence time is an open question (but it is finite): >= linear, <= exponential

the concept of Domination

For every state, if the value of it follows π₁ always equals or is larger than the value when it follows π₂, we say π₁ dominates π₂.
if π₁ dominates π₂ and there exits states that V^π₁(s) > V^π₂(s), we say π₁ strict dominates π₂.
if for every state, the distance between the value following policy π and following the optimal policy π* is no larger than ε, then π is ε-optimal.

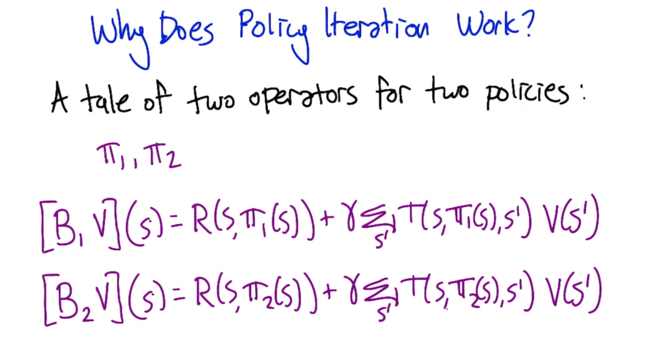
Why Does Policy Iteration Work

B₁ makes the update follows π₁ and B₂ makes the update follows π₂
Applying B operator to two Values will not make them further apart, if the two values are the same, applying B will not make them closer.

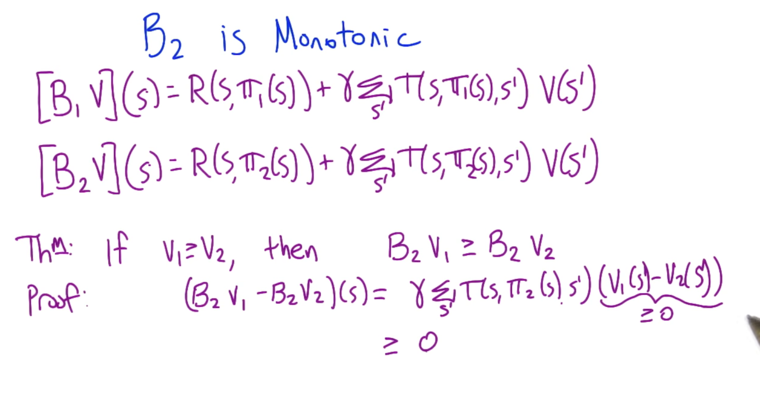
B<sub>2</sub> is Monotonic

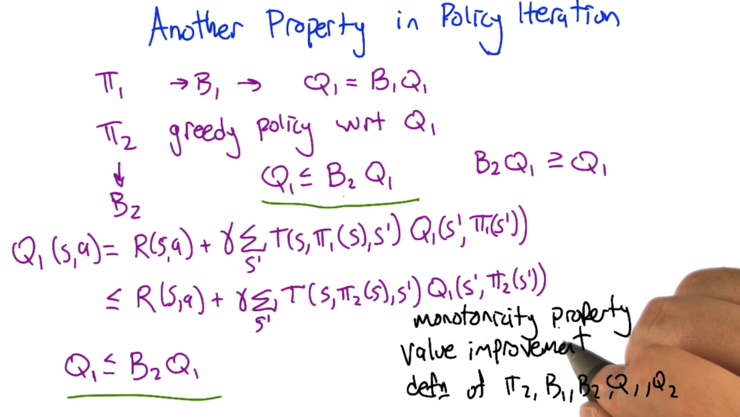
Q₁ is the fix point of B₁;
π₂ is greedy policy with respect to Q₁
B₂ is the Bellman operator of π₂
Applying B₂ (the greedy function wrt Q₁) on </sub>Q₁ will add a bound to Q₁, thus getting a better Q₁. This is called Value Improvement.

Quiz 1

Quiz 1 answers

Value improvement (or value non deprovement): for each state, value will improved until it could not get better anymore.
Monotonicity: Value can only get better after each iteration.
Transitivity: a >= b, b >=c, so a >=c.
Fixed point. If we apply B₂ over and over again on Q1, we will reach the fixed point of B₂,which is Q₂.

wrap-up

In Value iteration, greedy policy converges in finite step. This does not necessarily mean value function will converge.

2015-09-23 初稿
2015-09-26 完成
2015-12-04 reviewed and revised.