Reinforcement Learning (CS8803-O03)
Nov. 29, 2015
Solving Five-step Random-Walk problem with TD(λ)
TD-Lambda (TD(λ)), a machine learning algorithm designed for reinforcement learning problems, is invented by Richard S. Sutton(Sutton, 1988). Sutton performed two computational experiments on a 5-step random-walk problem to demonstrate the performance of TD(λ). This report is to replicate the experiments using the exact method described in Sutton’s paper.
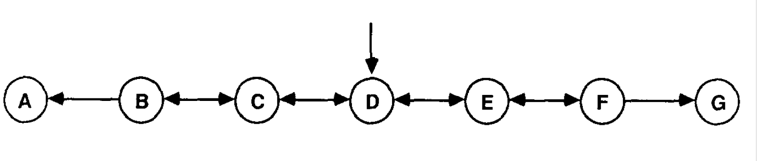
| The 5-step random-walk example consists of a Markov chain of 5 lined up states (B, C, D, E, and F) which are bounded by two extra absorbing states (A and G, Figure 1). For the non-absorbing states, the transition probabilities of moving to the right and to the right are both 0.5, and the ideal probability of a walk ending in state G from each state is: T = {1/6 2/6 3/6 4/6 5/6}, (e.g. p(G | B) = 1/6). The reward for states A and G are 0 and 1, respectively. The goal is to learn the estimated transition probabilities (a weight vector w) over a series of random-walks using the TD method. |
Method
To evaluate the performance of TD(λ) method, 100 training sets, each consists of 10 random-walk sequences, were generated. The root mean squared (RMS) error of w against the ideal predictions T were calculated and averaged across the 100 training sets.
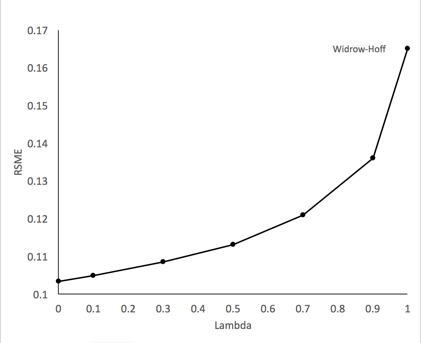
In experiment 1 (repeated presentation), each training set was fed to the learning algorithm repeatedly until converge. w will be updated only after the algorithm was trained on the 10 sequences in a training set. Sutton mentioned that TD(λ) will always converge when learning rate is small, but the learning rate or the convergence threshold were not reported. In this replication effort, learning rate (α) and convergence threshold (ε) were was to 0.05 and 0.0005, respectively. Smaller ε was tried but the implementation would get numerical overflow before converge.
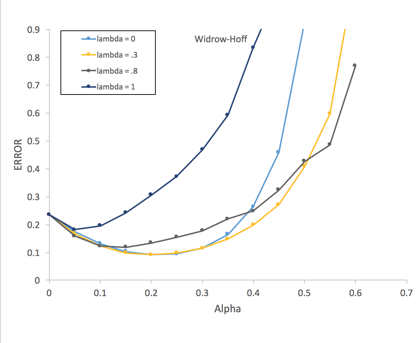
In experiment 2, the algorithm will see the training sets only once update w after each sequence. To demonstrate the effect of learning rate (α) on the performance of TD(λ), multiple learning rate were applied to the learning algorithm.
Results
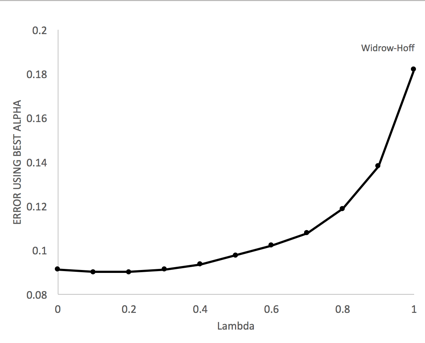
The main findings replicated Sutton’s original paper. In the repeated presentation experiment, the performance of TD(λ) declines as λ increases and TD(0) has the best performance. The error increases rapidly as λ approaching to 1 (Figure 2) with TD(1) has the worst performance. As shown in figure 3, the value of learning rate has evident effects on the performance of TD(λ) and most of the TD(λ) performed the best when α = 0.2 (the best α in Sutton’s original paper is 0.3). Figure 4 shows the best RMS error level of for each λ in TD(λ) when the best α is applied to the corresponding λ. In this case, TD(0) does not have the best performance any more, and TD(0.2) seems to have the best performance.
Discussion
This replication supports Sutton’s claims, but the results were not exactly the same as what’s in the original paper. For example, the range of RMS errors for experiment 1 was [.10 .17], the best α and best performer in experiment 2 were around 0.2 and TD(0.2), but in the original paper, they were [.19 .25], α = 0.3 and TD(0.3). This is not surprising for two reasons. A). Some parameters (α and ε) were not reported in the original paper; B). The training sets were randomly generated. α and ε can affect the converging process and the distribution of random-walk sequences will affect the learning results.
In conclusion, the replication supports the claims of the original paper.
Reference
Sutton, R. S. (1988). Learning to predict by the methods of temporal differences. Machine learning, 3(1), 9-44.