Machine Learning笔记 第04周

• SL8: VC Dimensions
• Bayesian Learning
• Bayesian Learning
•  Bayesian Learning in Action
•  Bayesian Classification

Week 04 tasks：

• Lectures: VC Dimensions and Bayesian Learning.
• Reading: Mitchell Chapter 7 and Chapter 6.

SL8: VC Dimensions

• Lesson 08 Notes
• VC Dimensions Review

• m>= 1/ε( ln

  H

  +ln(1/𝛿) ). Here the sample size m is dependent on the size of hypothesis

  H

  , the error ε and the failure parameter_ 𝛿_. What happens if

  H

  is infinite?

• quiz 1: Which Hypothesis Spaces Are Infinite

• In the example above, although the hypothesis space is infinite (syntactic), we can still explore the space efficiently because a lot of hypothesis are not that meaningfully different (semantic).

• VC dimension: what is the largest set of inputs that the hypothesis class can shatter.
• Vapnic-Chervonenkis

• not sure how to answer this question. need to rewatch.

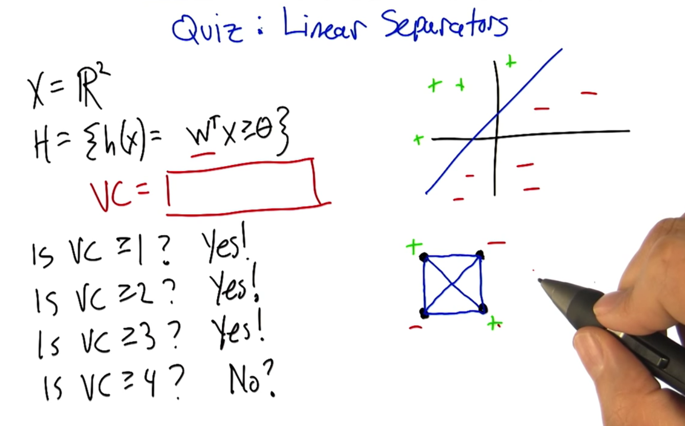
• Here VC = 3.

• the vc dimension is going to end up being d plus 1 because the number of parameters needed to represent a d dimensional hyperplane is __ d plus 1__.

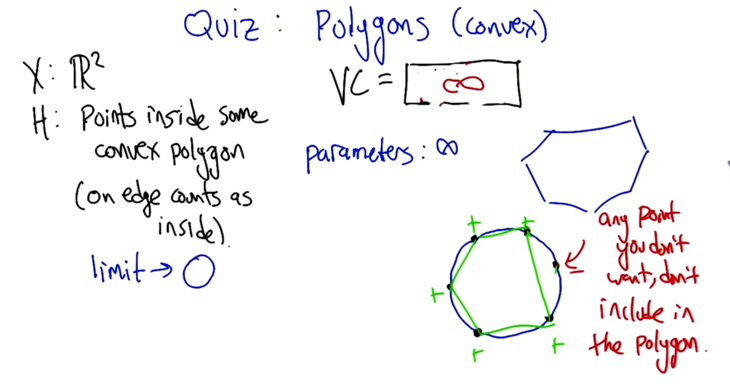
• if the hypothesis is that points inside some convex polygon, then the VC = infinite.

Bayesian Learning

• Lesson 09 Notes
• Bayesian Learning Extension

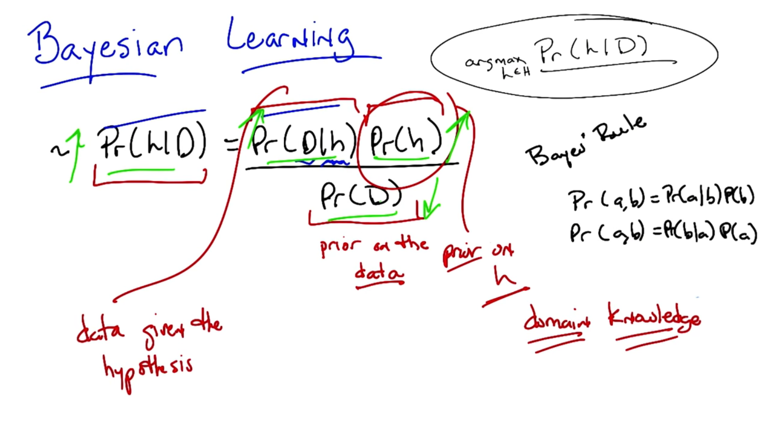
• the best hypothesis is the most probable hypothesis given data and domain knowledge.

• argmaxh∈ H Pr(h

  D)

Bayes Rule

• Bayes Rule: Pr(h

  D) = Pr(D

  h)Pr(h)/Pr(D)

  • Pr(D) is the prior about data
  • Pr(h) is the prior of hypothesis, and it’s the domain knowledge.

  • Pr(D

    h) is the possibility of data given h, it is much easier than Pr(h

    D) to compute.

• comparing the probability of one having /not having spleentitis.

Bayesian Learning

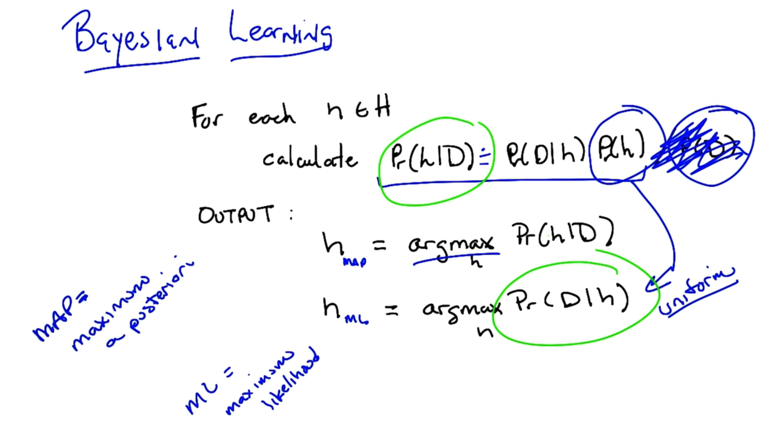
• to find the largest Pr(D

  h), we could drop P(D) for the bayes rule because it doesn’t matter since our task is to find the best h. MAP: maximum a posterior.

• If we don’t have a strong prior or we assume the prior is uniform for every h, we can drop Pr(h). ML: maximulikelihoodod_
• the hard part is to look into every h
• Since H is often very large, this learning algorithm is not practical

 Bayesian Learning in Action

• given a bunch of data, your probability of a particular hypothesis being correct, or being the best one or the right one, is simply uniform over all of the hypotheses that are in the version space. That is, are consistent with the data that we see.

• given <x,d> pairs, and d_i =k * x_i which has a probability of Pr(1/2^k), what is the probability of D given d.

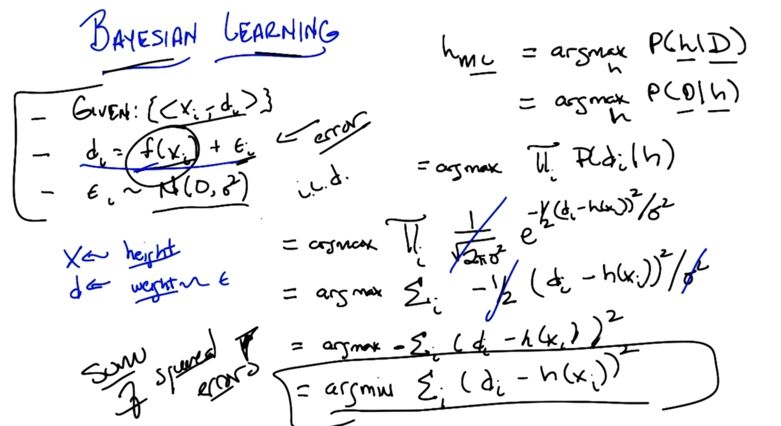
• given training data, figure out f(x) and with its error term. If the error can be modeled by Gaussian function, then
• h_ML can be simplified to minimizing a sum of squared error.

• find best hypothesis from the three.
  • calculate and compare squared error.

• hMAP can be transformed to minimize the length of hypothesis (size of h) and the length of the D

  h (which is misclassification error)

• there is a tradeoff between size of h and error. this is called minimum description length
• there is a unit problem: unit of error and size need to be figured out

 Bayesian Classification

• when we do the Classification, we will have each hypothesis to vote

• Bayes optimal classifier = weighted voting by h.

2016-02-08 SL8 完成
2016-02-08 凌晨，SL9 完成.第一稿发布