Machine Learning笔记 第06周

• Optimize Me
• Optimization Approaches
• Random Restart Hill Climbing
• Annealing algorithm
• Genetic Algorithms
• MIMIC
• Finding Dependency Trees

Week 06 tasks:

• Lectures: Randomized Optimization.
• Reading: Chapter 9 of Mitchell, as well as the overview on the No Free Lunch Theorem.

• optimization is to find a x^* in input space X to make the objective function has the maximum (or close to maximum).

Optimize Me

• The first question, since the input space is small, we can plot the function and find the largest f(x).
• the second the functions, we can try to use calculus: Set the derivative f(x) to 0 and solve the derivative function ( which will be hard to solve since it’s a cubic function). Alternatively, we can try to plot the data using subgroup of x.

Optimization Approaches

• Three approaches:
  • generate & test: when we have a small input space but a complex function
  • using calculus: when the function has derivative and the derivative function is solvable when its value is set to 0
• Newton’s method: when the function has derivative and it can be improved iteratively.
• When these approaches does not work, then Randomized Optimization.

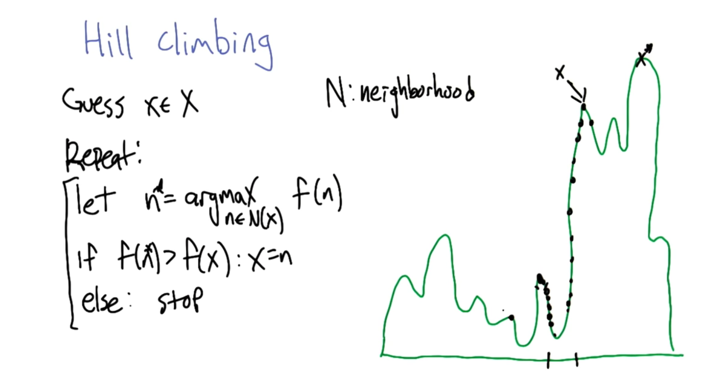
• the hill climbing algorithm will stuck at a local maxima.

Random Restart Hill Climbing

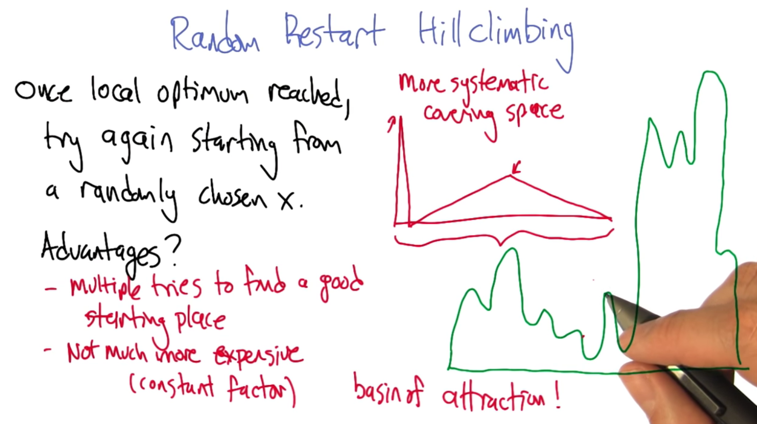
• how to avoid the unlucky starting point?
  • checking and make sure the starting point is not visited before
  • make sure the starting point is faraway from known local maxima

• The six points under the maxima hill are special
  • 4 points under the global maxima will take average 4 steps to get to the global maxima. and that’s the 4/28*(4)
  • the 2 basin points, half of the time will lead up in global maxima, and half of the time will lead to local maxima (and restart).
• all the other 22 points will lead to local maxima and then start a new round with a randomized starting point.
• if keep track of the points visited, the algorithm might do better than 28 on average.
• if the attraction basin under the local maxima is large, hill climbing will do better.

Annealing algorithm

• One step further than hill climbing: allow downwards to “explore”

• if f(x_t) and f(x) is very close, then f(x_t) -f(x) is close to 0 and p will be 1.
• If T is really big, say infinity, then f(x_t) -f(x) doesn’t matter then. P will be 1, and x will jump to x_t
• if T is really small, close to 0, p will climb, not jump.

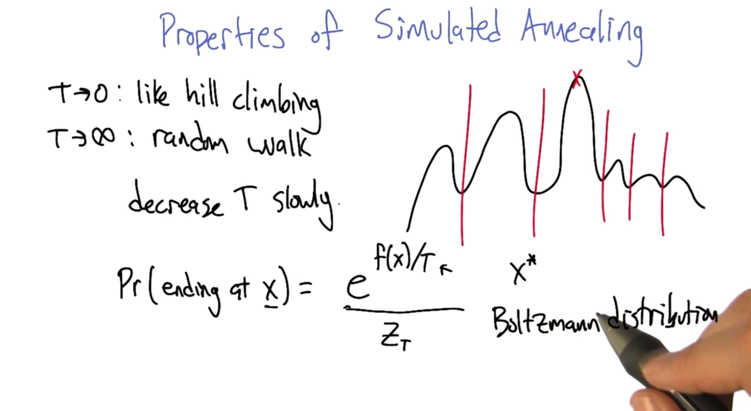
• T -> 0: like hill climbing
• T-> ∞: random walk
• Desearse T slowly: As T decreases, it’s harder and harder to jump over local maxima, and algorithm will reach global maxima

Genetic Algorithms

• GA is like random restart but doing the restart in parallel.
• Crossover - population holds information.

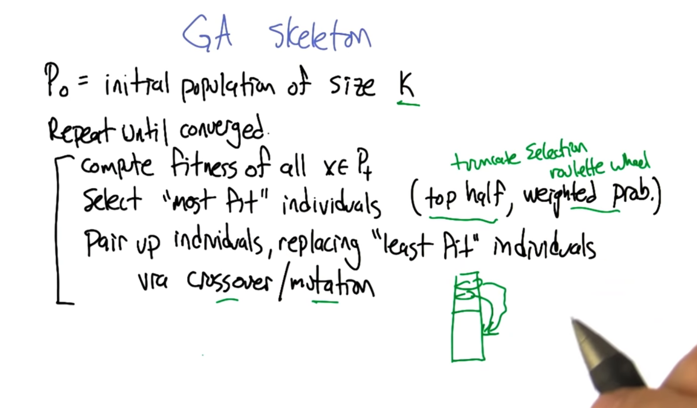
• Define “most fit”
  • top half or truncate selection:the half individuals with the largest score
  • weighted prob. or roulette wheel: weighted fitness function with probability.
• what’s crossover?

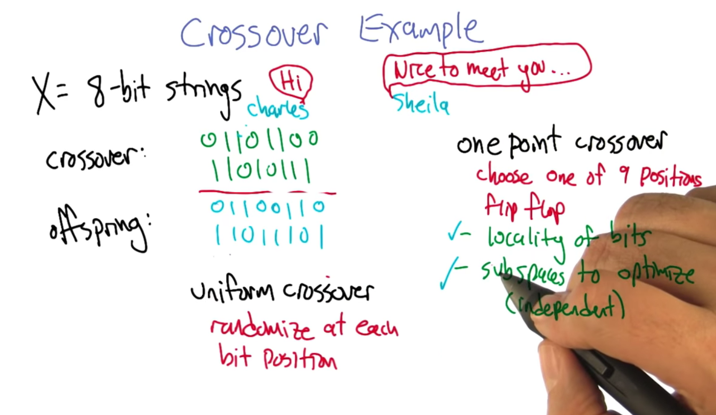
• Uniform crossover: randomization at each position

MIMIC

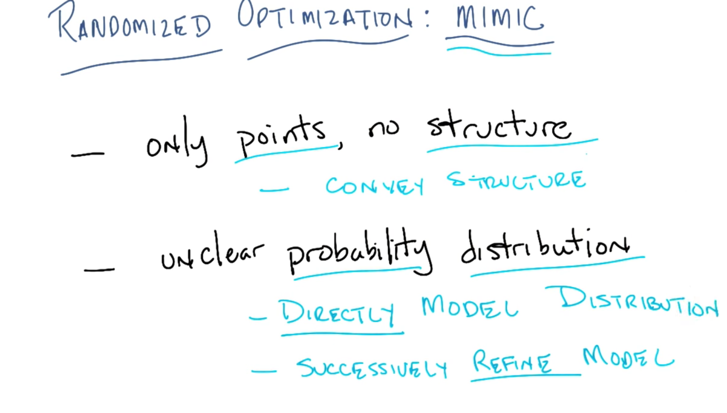
• Charles’ paper on MIMIC

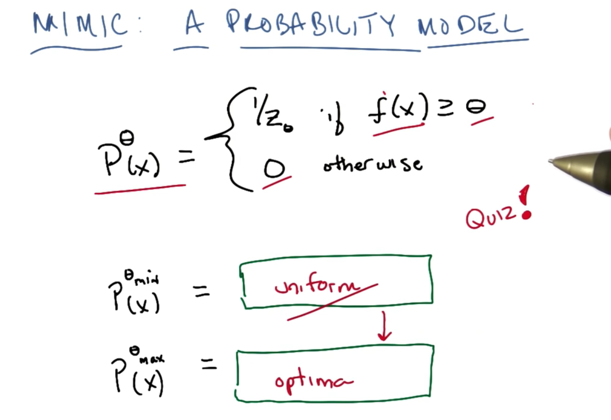
• when θ is min, then P is the uniform distribution of X
• when  θ is max, we get the maxima or optima of the distribution

• Given a threshold θ_t, generate samples from P^θ_t(x), then set θ_t+1 to be n^th percentage and retain only those samples, s.t. f(x)>=θ_{t_1}
• instead of using these samples, we estimate P^θ_t+1(x), and then generate new samples from it. then repeat the process again and again until converge.
• Two assumptions:
  • P^θ_t(x) is estimable
  • P^θ_t+1 is close enough to P^θ_t
• this is a lot like Genetic algorithm but P^θ and P^θ＋ ϵ can preserve the structure.

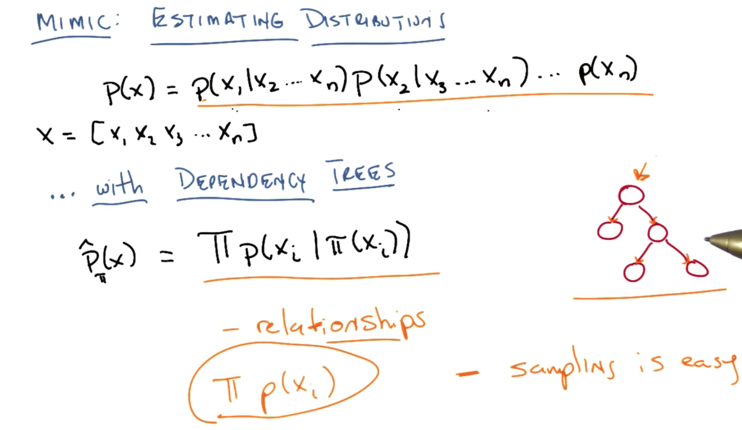
• P(x) is the combination of the p of each x in X=[x1 x2 …. x_n] given others in X. To estimate P(x) this way, we will need huge amount of data ( exponential to n).
• Dependent tree: each node only have one parent.
  • it can represent relationships
  • and sampling dependent tree is easy
  • it’s a general form of crossover and it does not require locality.

Finding Dependency Trees

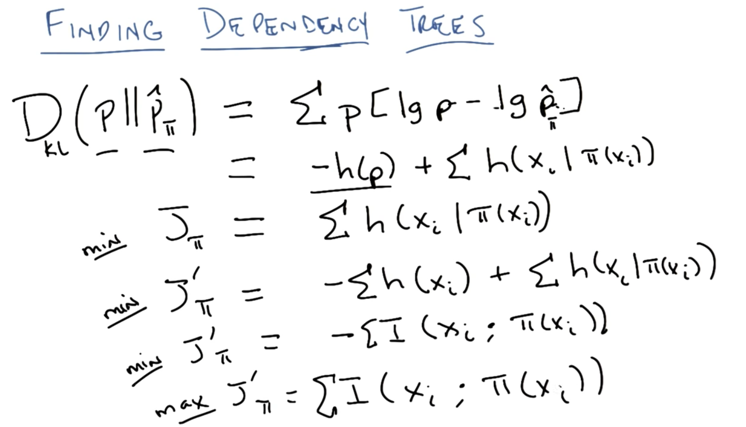
• Minimize Divergence of P and P_hat_π, Divergency can be written as entropy.
• build a cost function by remove -h(p) and add entropy -h(x_i), then we get the mutual information between x and π
• Finding Dependency Trees is now converted to a problem to maximize mutual information between x and it’s parent. or in another word, to find the parent who knows the most about the node.

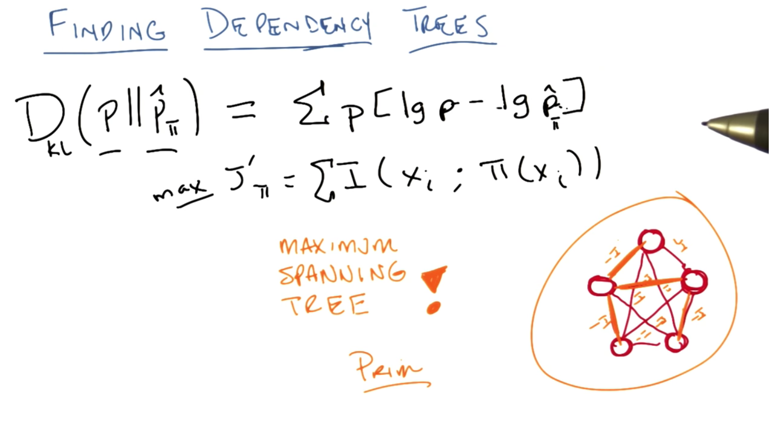
• This can be solved by solving the maximum spanning tree. Using Prim.
• The prim algorithms is fairly fast algorithm ( polynomial to the number of edges of a graph) and it’s good for dense connected graph.

• dependent tree is used to estimate P given the samples from the previous step.

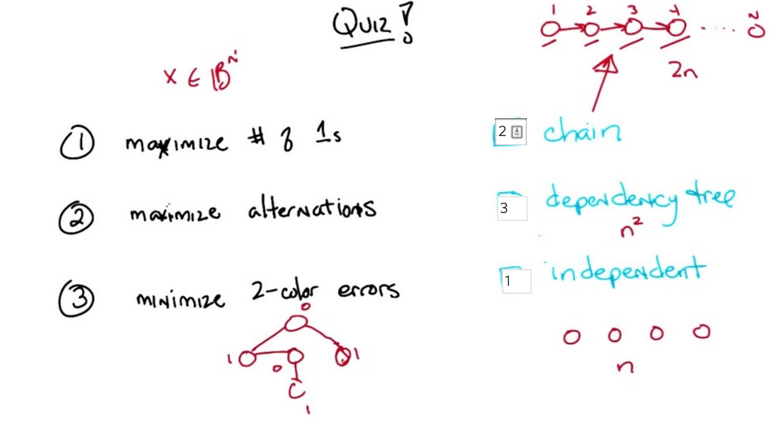
• what distribution can represent the maxima of the problems on left column.

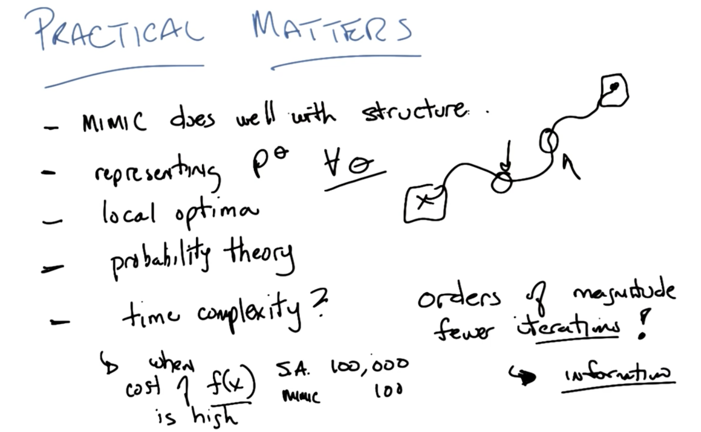
• MIMIC evaluate cost function less when comparing to Simulated Annealing, but it usually takes longer to run.
• MIMIC will get more information in and out

2016-02-17 完成 Genetic Algorithms
2016-02-19 初稿