Machine Learning笔记 第08周

• Basic Clustering Problem
• K-means
  • K Means in Euclidean Space proof
• Soft Clustering
• Clustering Properties

注意，第七周是考试周，我其实把考试的的内容压缩进了第06周的笔记中去，所以第七周没有单独笔记。但是所有课堂内容没有缺失，特此声明。

Week 08 tasks:

• Lectures: unsupervised learning:  clustering and expectation maximization.
• Reading: Chapter 6 of Mitchell, and the supplementary notes on Expectation-Maximization and clustering.

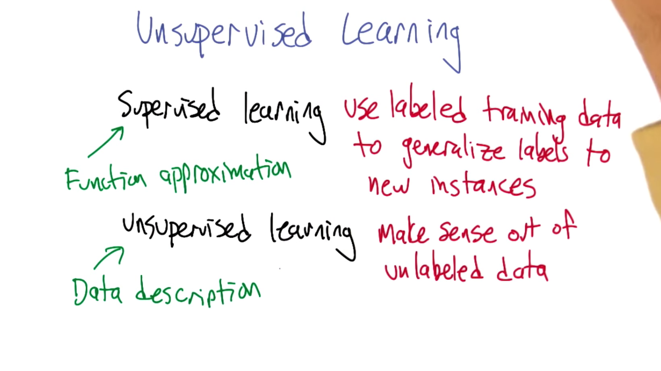
• Supervised learning: use labeled training data to generate labels to new instances. Can be seen as function approximation.
• Unsupervised learning: make sense of unlabeled data. Data description, when new instance presents, describe it with the generated data description.

Basic Clustering Problem

• definition: given set of object X and inter object distance D(x,y) = d(y,x), we can partition the input and put x and y into the same cluster when P_D(x) = P_D(y)
• extreme cases: when P_D(x) = 1, then will be only one cluster; when P_D(x) = x, then each x is a cluster (each cluster has only one item).

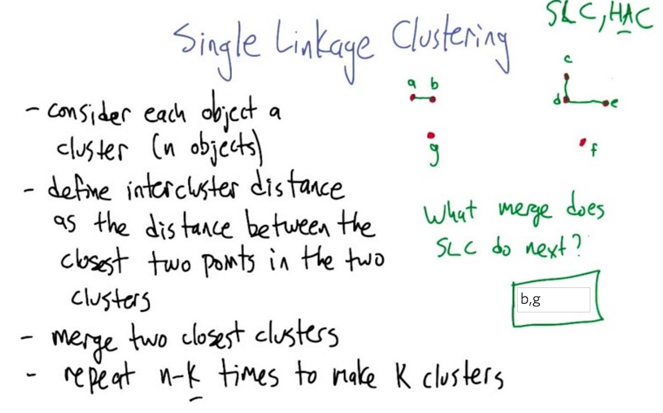
• Single Linkage Clustering: first define each object as a cluster, and then find out the closest two points and merge them ( like kNN). The distance function could be customized. Repeat N-k times can get k clusters
• k is prior knowledge
• quiz, what two points should be linked together next?

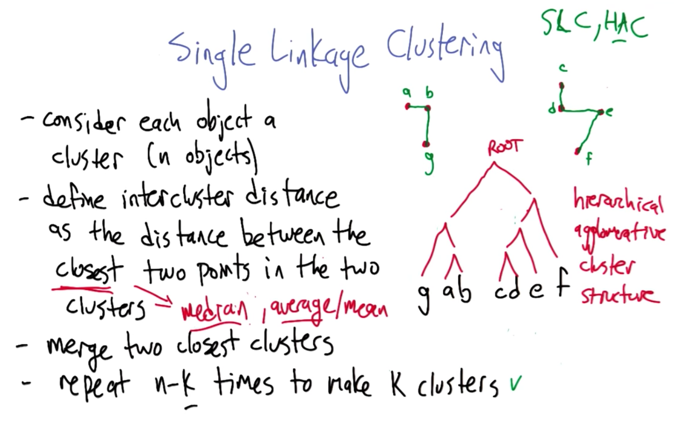
• the clustering process could be represented as a hierarchical tree structure
• the distance function could be mean, median…

• For SLC, we need to look at each pair can find the one has the smallest distance and this is a O(n²) process. And we need to do this about n times. So the answer is O(n³)

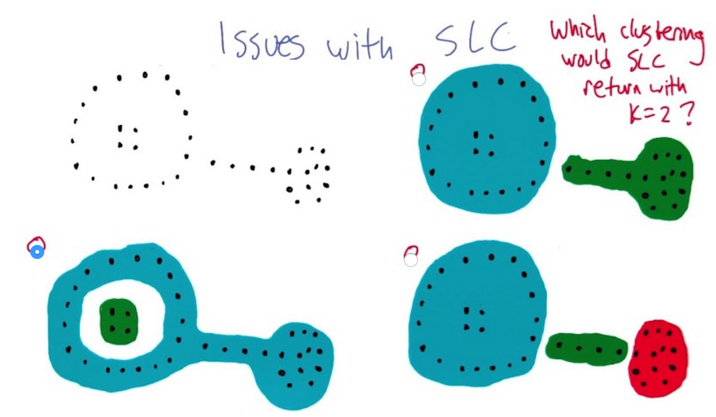
• SLC could not clustering this problem correctly

K-means

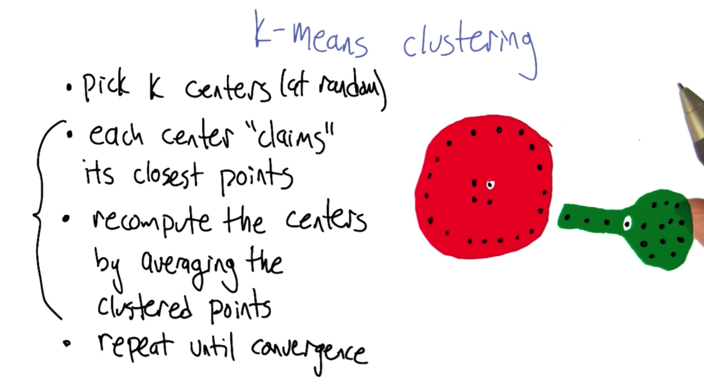
• randomly initialize k centers
• each center claims points to cluster the data
• recompute the center by average the clustered points
• repeat above until converge.
• Question: does it always converge?

K Means in Euclidean Space proof

• Terms: partition, cluster and center

Not sure how to understand the definitions here.

• the error can never go up for partition part and re-centering part of the clustering process
• given the that the partition/clustering space is finite, K-means will converge in finite time.

• it’s possible for K-means to stuck at a local optima, but this can be solved by random restart ( like random hill climbing in the optimization)

Soft Clustering

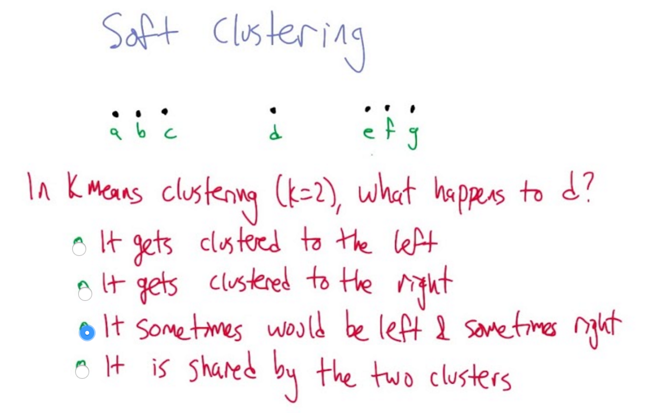
• K-means and SLC could not give the point d a definitive cluster
• Solution: lean on possibility :)

• here ML is maximum likelihood.

• Hidden variables are used to keep track which Gaussian distribution that x is generated from

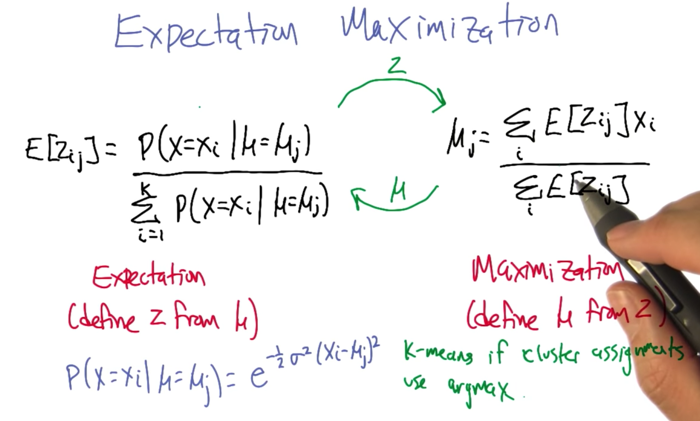
• there are expectation and maximization for the soft clustering. The probability of X_i in the _i cluster is between 0 and 1.
• soft clustering can be converted to K-means if push the probability to be 0s and 1s.

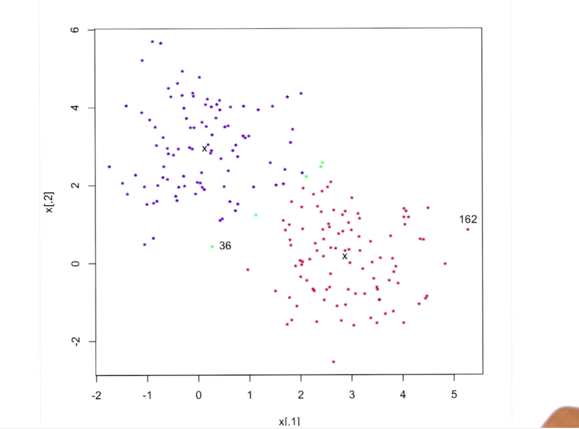
• given K, randomly generate k centers
• with each iteration, the centers were recalculated and the probability of the each point is in a cluster is also updated until converge.

• the reason that EM does not converge is because there are infinite number of configurations.
• Local maxima problem can be solved by random restart
• E, M might be different for different problems

Clustering Properties

• It’s not possible to have all three properties.

2016-03-02 初稿, SLC
2016-03-14 K-Means
2016-03-15 EM