• I need to read the book to understand this chapter.
• challenge question
• Map Coloring problem
• Constraint Graph
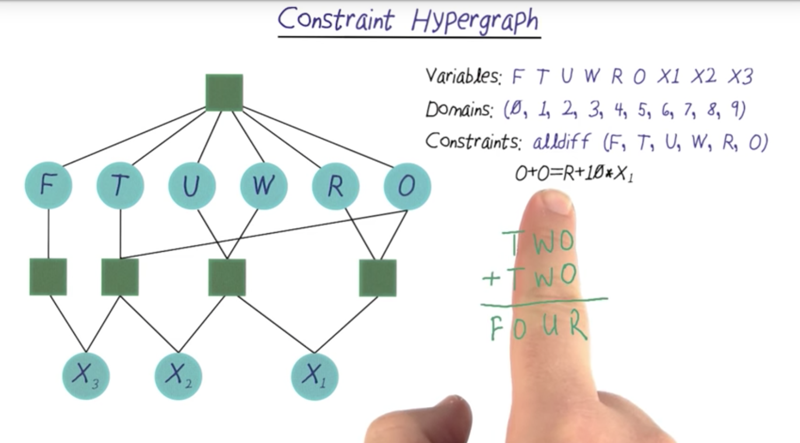
• Constraint Hypergraph for the challenge question
• Backtracking Search
• quiz
• forward checking
• Structured CSPs
• Iterative Algorithms
• the challenge question

This week: watch Lesson 4, Constraint Satisfaction, and read Chapter 6 in AIMA (Russell & Norvig). Assignment 2: Tridirectional Search **Due: September 24! Here is the GitHub repo.  

I need to read the book to understand this chapter.

challenge question

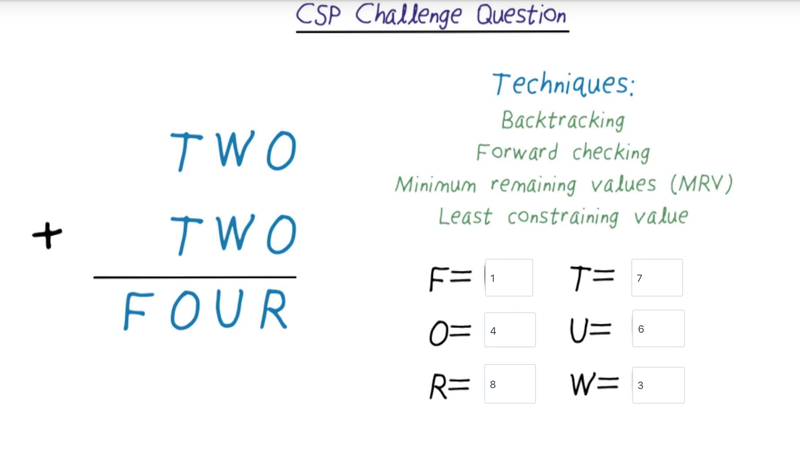
• use the techniques mentioned in the quiz to solve a problem like this

Map Coloring problem

• question: color the map with a minimum number of colors while no states adjacent will be colored the same.

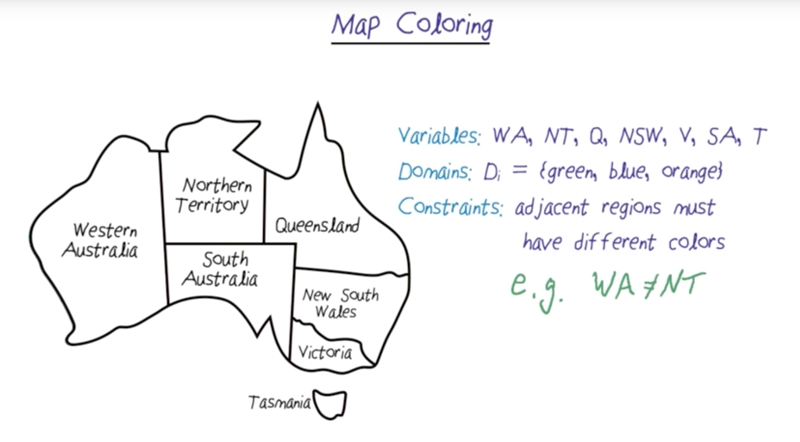
The map-coloring problem has the following components:

1. Variables
2. Domains
3. Constraints: or rules to specify the problem.

• Unary constraints concerns only one variable.
• The problem can be illustrated by a Constraint Graph if the constraints are binary.

Constraint Graph

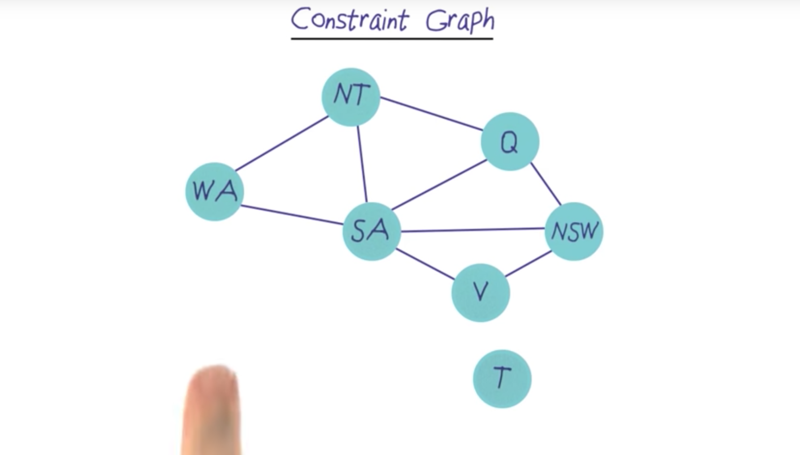
1. Nodes are variables
2. Arc (Edges) represents constraints.

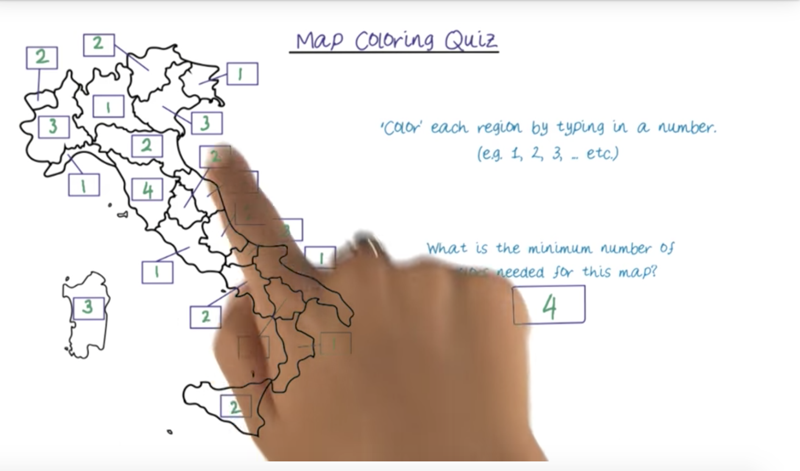
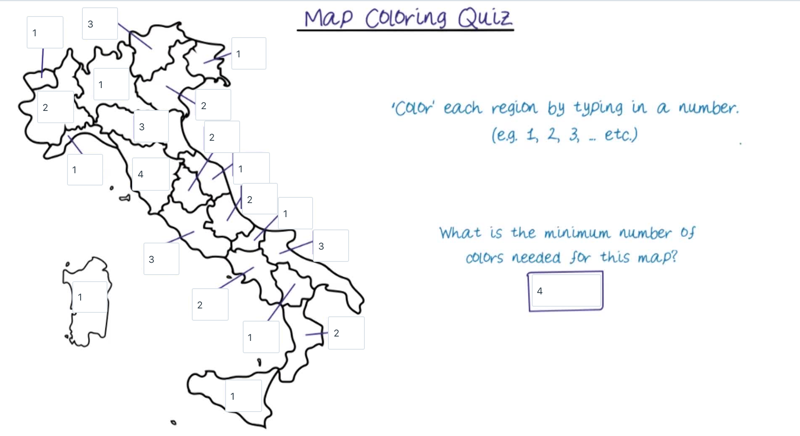
There are multiple solutions to the quiz. But all the solutions must follow the rules (satisfy the constraints).

• Constraints can be multi-nary and soft constraints.

Constraint Hypergraph for the challenge question

Backtracking Search

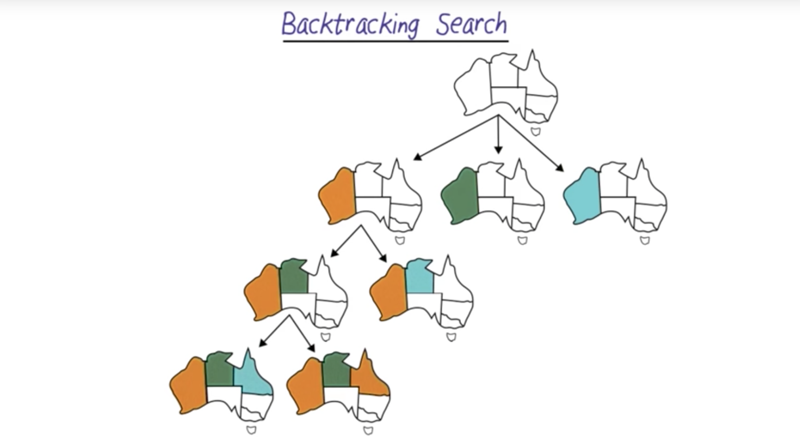
• backtrack search is like depth-first search, it goes deeper and deeper until it reaches a “dead-end”
• In case of dead-end, the algorithm backtrack up to the upper division to try another branch.
• repeat these steps until the solution is reached.

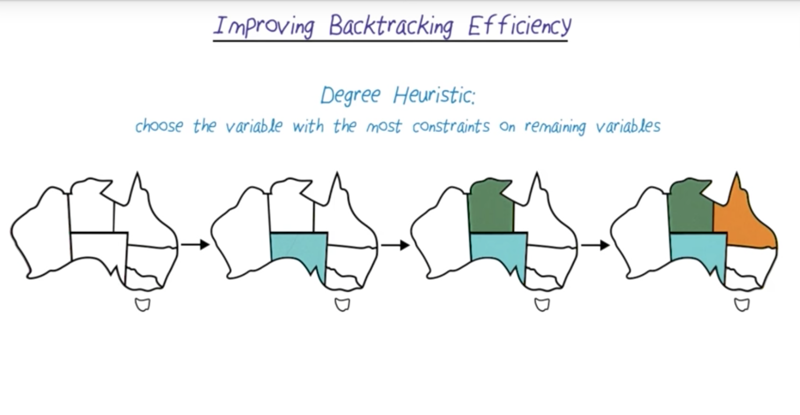
There are ways to improve the search efficiency

1. choose the least constraining value for each step
2. choose the variable with the fewest legal values

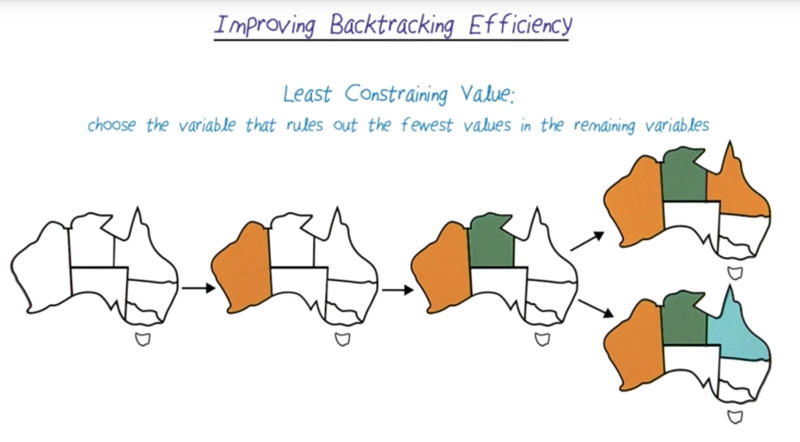
• in the image above, in the branching step, which area should we choose to color? Least constrain value will choose the right-upper corner because it has more color to choose from. if we choose orange again, we will leave green to be unused (or lest constrained).

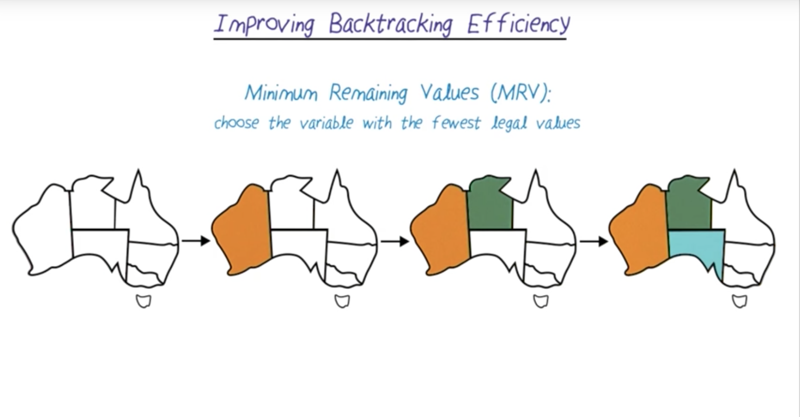[Minimum remaining values]: or we can choose the middle-lower region because it has the least color to choose from. When there is a tie, a heuristic could be used to select the next step/ area to explore.

quiz

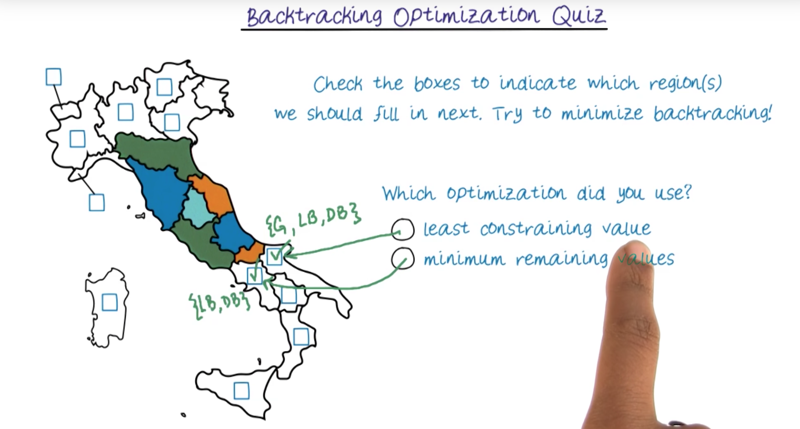
• we can use minimal remain values to choose the region adjacent to the red and blue blocks because this will make it region only have 2 colors to choose from (minimum remaining values)
• Or we can choose the one on the top if it since it only has one color to choose from (least constraining values) since it only have Green to use.

forward checking

• we can also use forward checking as a warning system for dead-end branches

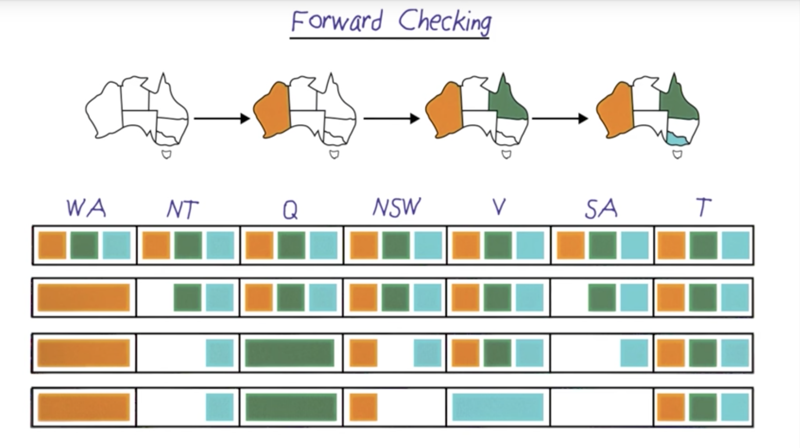
• forward checking keeps track of the available domain for each variable in each step
• a dead-end is reached when there is no domain for an unresolved variable.

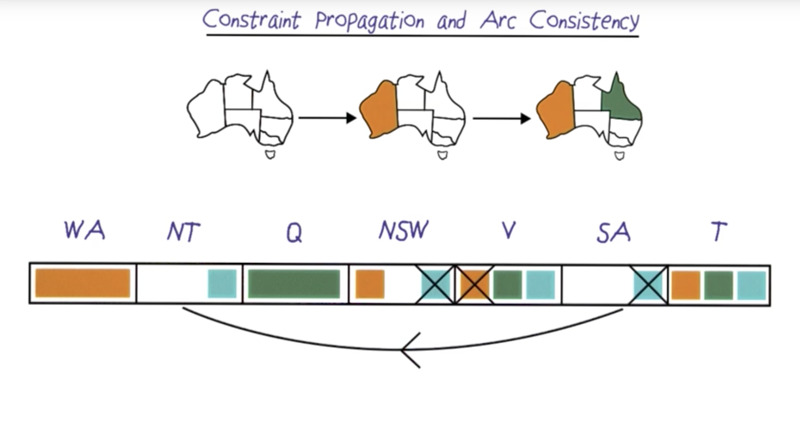
• Arc Consistency: all the variables have at least a value in the possible domain.
• Neighbors should not have the same color, thus a selection of a color can have a chain effect on the domain for variables.
• when we find a region has no value available to assign, return ‘Failure’ to the problem.

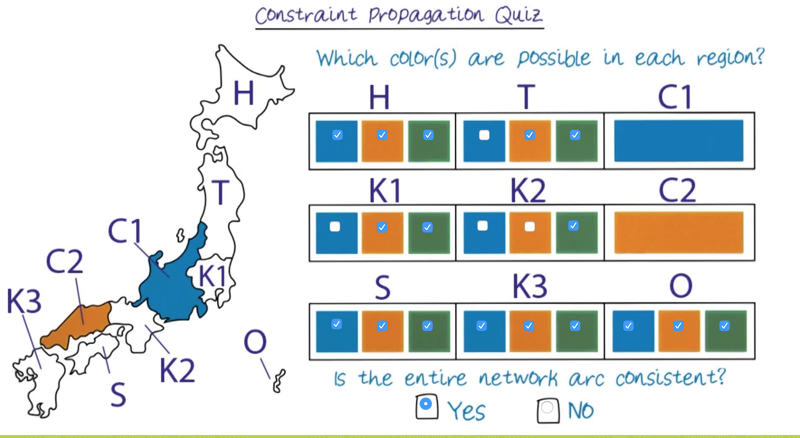Question: select all the possible values for each region and indicate whether the entire network arc consistent or not.

Structured CSPs

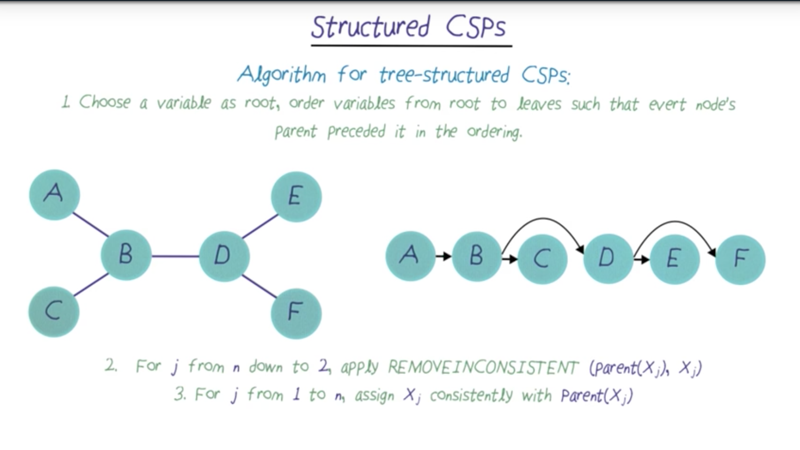
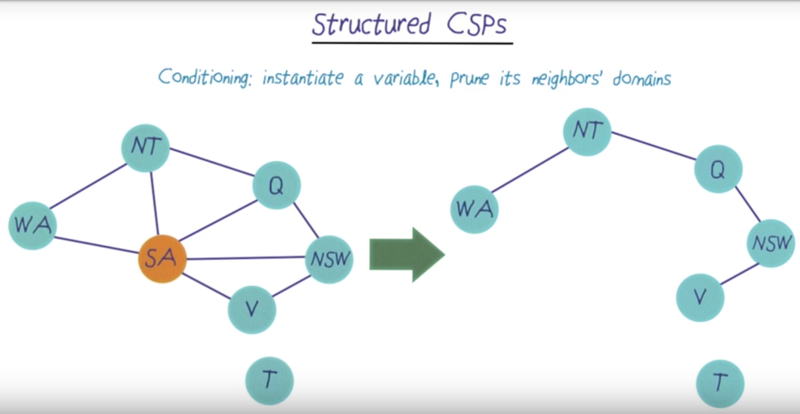
• How fast the algorithm will be?

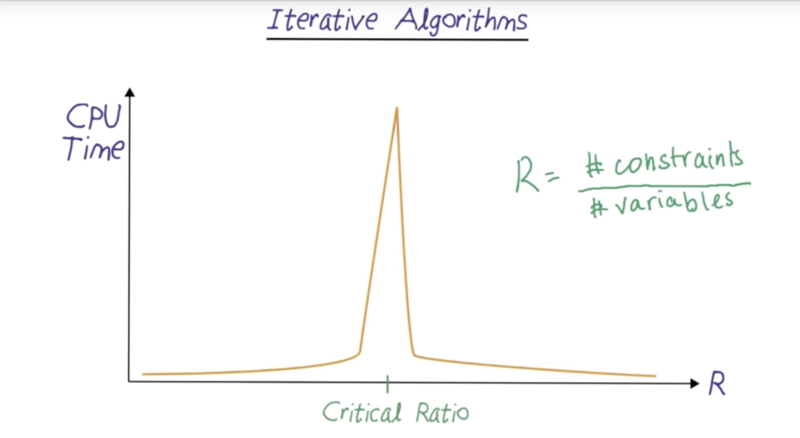
Iterative Algorithms

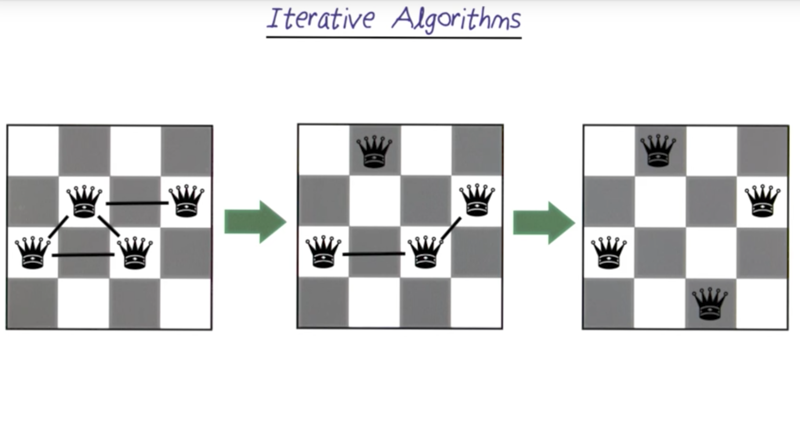
• Iterative Algorithms works very well then the solutions are plenty or very few.
• the problem becomes hard to solve when the ratio of constraints and solutions reaches a critical ratio

the challenge question

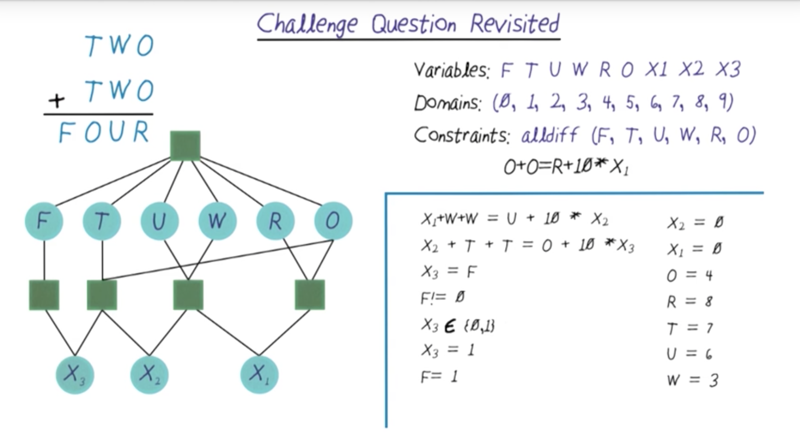
can be resolved by forward-checking: checking the available domains for values.

#s Readings

AIMA: Chapter 6