• Challenge question
• Intro To Probability And Bayes Nets
  • outline
• Probability / Coin Flip
  • Summary
• Dependence
• quiz: Weather
  • Quiz: Cancer
• Bayes Rule

Week 6 Announcement

This week you should watch Lesson 5, Probability, and read Chapter 13 in AIMA (Russell & Norvig). Assignment 3:  Bayes Nets Sampling

Challenge question

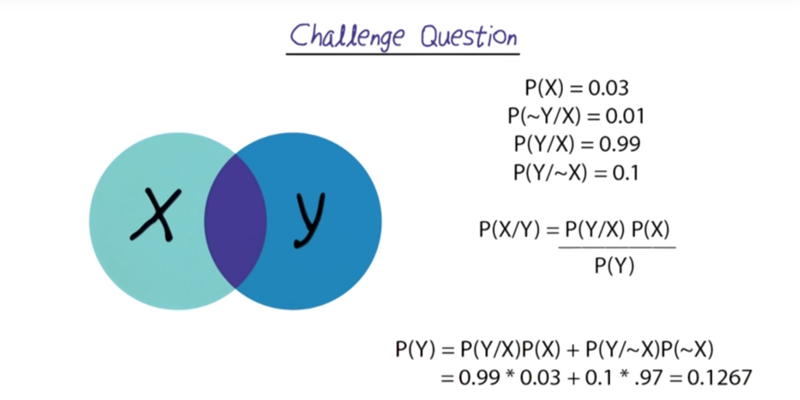
• P(x) is the probability of the disease without other constraints

• P(Y) is calculated P(Y

  ~X)P(~X) + P(Y

  X)P(X)

Intro To Probability And Bayes Nets

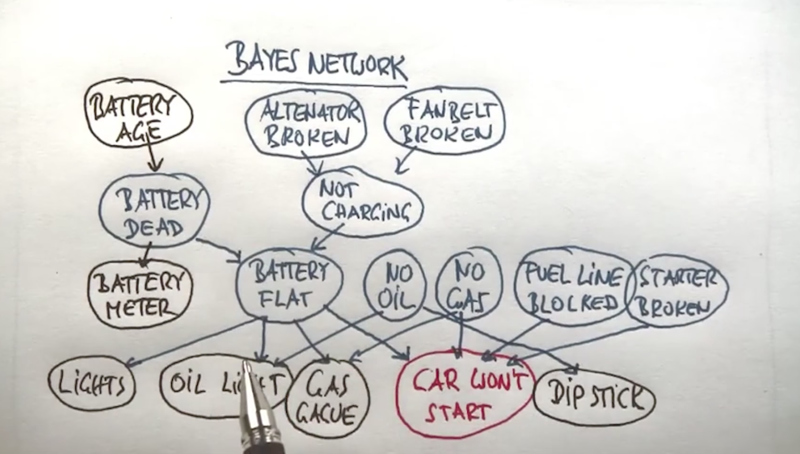
• in the above example, we have random variables represents events which are connected by arrows to describe the relationships.
• the arrows indicate that the child nodes are influenced by their parents, and the influence can be a deterministic or probabilistic way.
• Bayes net is a compact representation of the distribution of the large probability distribution of all the variables.
• With Bayes net, we can specify the distribution, observe certain variables and compute probabilities of unobserved variables.

outline

Probability / Coin Flip

• P(T) = 1 - P(H)
• since H and T are independent events, P(H,H,H) = P(H) x P(H) x P(H)

• remember, P(H) and P(T) are independent

Summary

Dependence

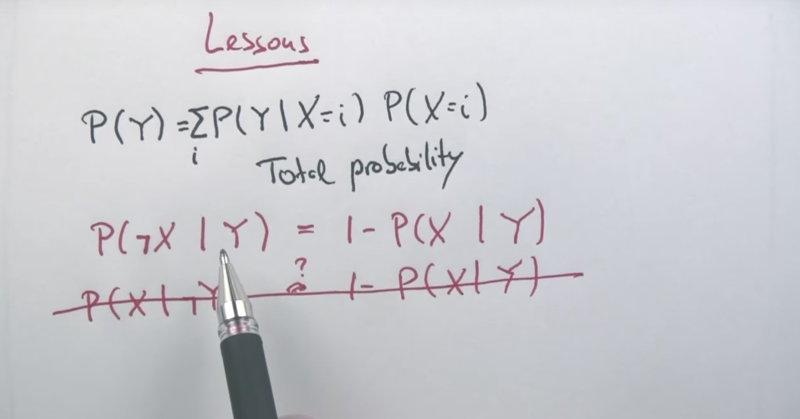
quiz: Weather

• complementary rule applies for the first 2 quiz questions.

• dependence rule applies to the calculation of P(D2 = Sunny) and P(D3 = Sunny)

• P(D2 = Sunny) = P(D2 = Sunny

  D1 = Sunny) x P(D1 = Sunny) + P(D2 = Sunny

  D1 = Rainy) x P(D1 = Rainy)

• Simillarly, * P(D3 = Sunny) = P(D3 = Sunny

  D2 = Sunny) x P(D2 = Sunny) + P(D3 = Sunny

  D2 = Rainy) x P(D2 = Rainy)

Quiz: Cancer

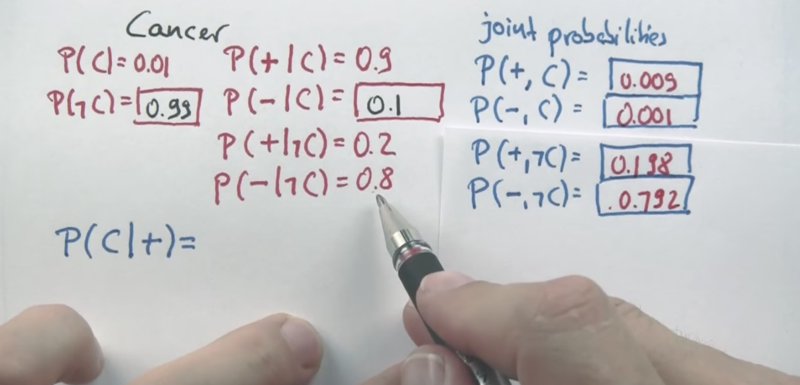
• joint probability of a and b is P(a, b) = P(a) x P(b)

• P(C	+) = P( +,C) /(P(+,C) + P(-,C))

• this is the Bayes rule!

Bayes Rule

• Prior
• Posterior
• Likelihood
• Marginal likelihood (Total probability)

20171006 初稿