- Introduction
- Planning Under Uncertainty MDP
- Robot Tour Guide Examples
- MDP Grid World
- Problems With Conventional Planning 1
- Policy Question
- MDP And Costs
- Value Iteration
- Quiz
- Value Iterations And Policy
- MDP Conclusion
- POMDP Vs MDP
- POMDP
- Readings on Planning under Uncertainty
Introduction
This lecture will focus on marrying planning and uncertainty together to drive robots in actual physical roles and find good plans for these robots to execute.
Planning Under Uncertainty MDP
- Planning + uncertainty: MDPs (Markov decision process) and POMDPs (partially observed MDP)
- Planning + uncertainty + learning: Reinforcement Learning
Methods categorized based on the characteristics of the world (observability and certainty).
- MDP deals with situations where the world is stochastic and fully observable.
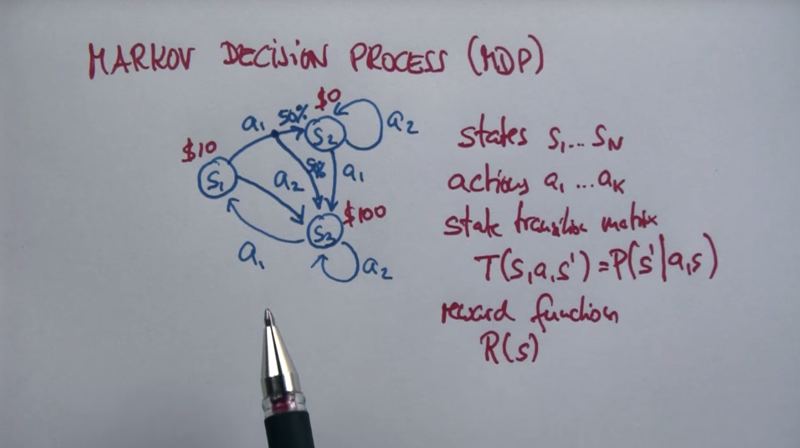
- MDP has states, actions and state’s transition matrix and a reward function. (it can attach to state, or action or transition?)
- it becomes Markov if the outcomes of actions are somewhat random.
- planning problem is depended on actions to each possible state. But the operational goal becomes maximizing total reward.
Robot Tour Guide Examples
All these robots need to deal with uncertainties and observabilities to do their jobs (tour guide or mine explorer).
MDP Grid World
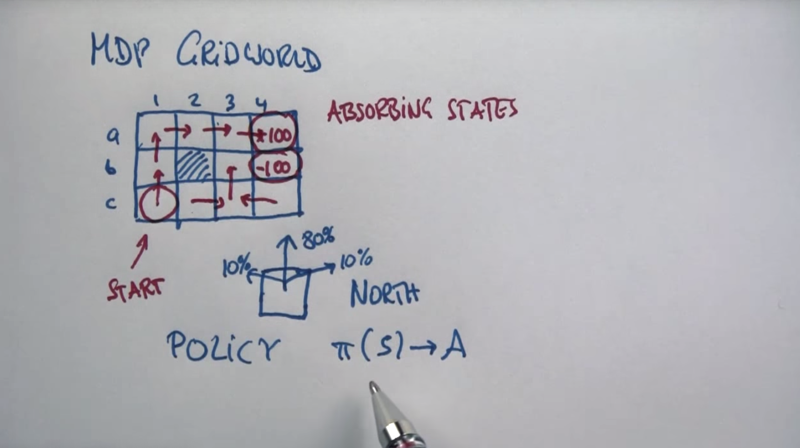
Absorbing states: search will end if the agent is at the absorbing states. Policy assign action based on the state the agent is in.
Problems With Conventional Planning 1
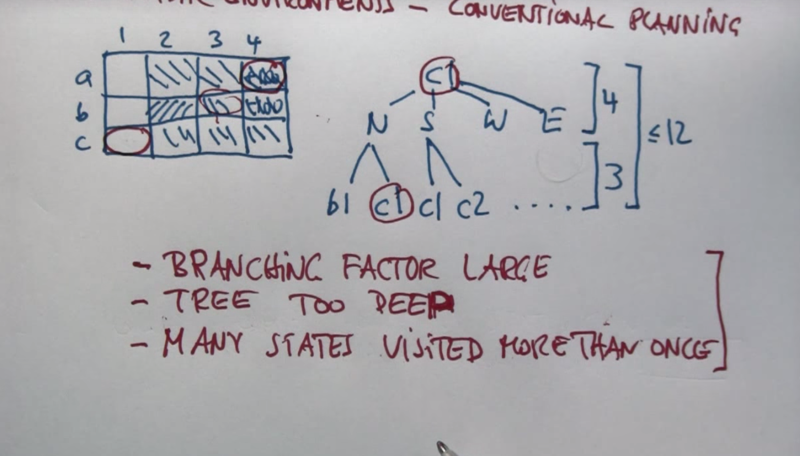
Policy Question
Question: what is the best action to take when an agent is in states a1, c1, c4 and b3?
MDP And Costs
The reason that the agent should be avoiding the b4 state is the cost.
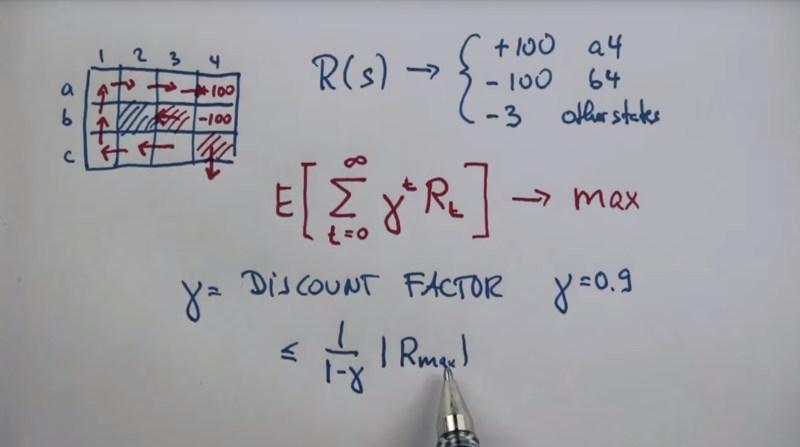
- The goal is to find the best path wich cost less with finite steps.
- The discount fact can bound the max result.
Value Iteration
- value function can determine the policy based on the total reword.
- The value function is a potential function that leads from the goal location all the way into the space so that hill climbing in this potential function leads you on the shortest path to the goal.
- The algorithm is a recursive algorithm and it converges, and you have a grayscale value that really corresponds to the best way of getting to the goal.
Quiz
Determistic question:
I Quiz: calculate Value when an agent was at each state.
Stochastic Question :
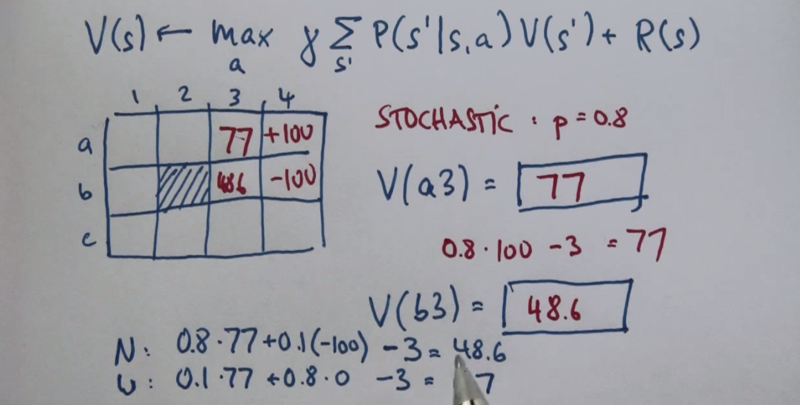Calculation is complicated here because the reward of each action must be evaluated.
Value Iterations And Policy
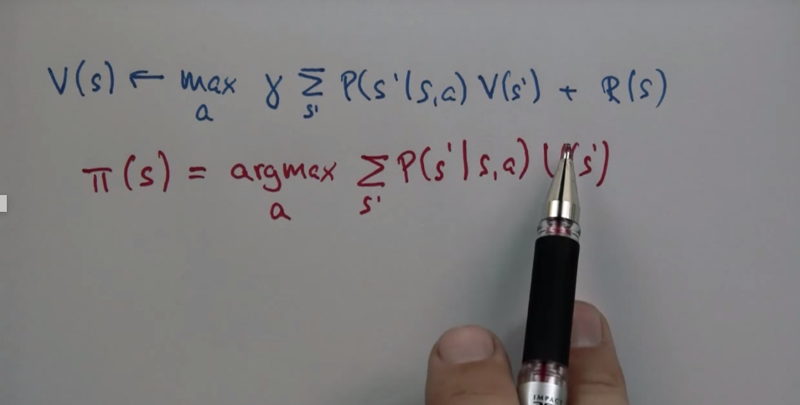
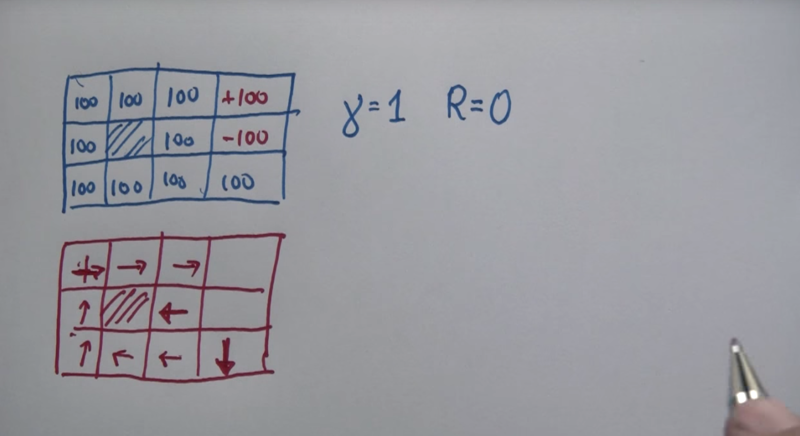
The policy can be defined by the value function after the value of each cell is calculated. The action policy is to choose the action which leads to the highest path reward.
If the cost of each state is positive, the policy will encourage action to stay in the current state.
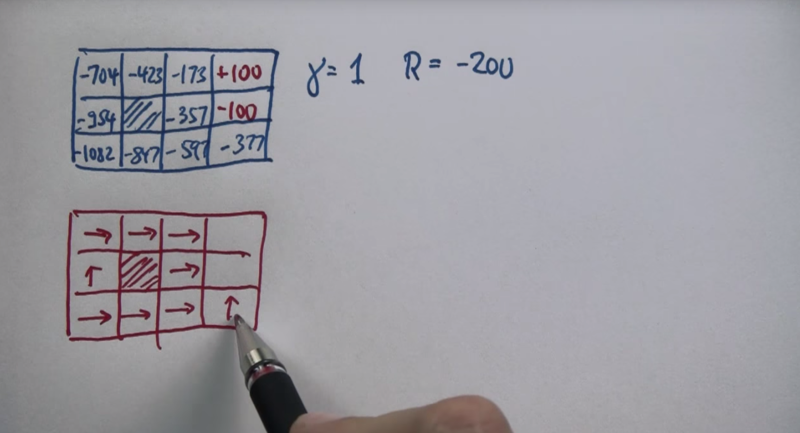
If the cost is too low, the value of each state might become so low that the agent will try to end the search as soon as possible without looking for an optimal solution
MDP Conclusion
POMDP Vs MDP
- MDP is for fully observable environments and planning in stochastic environments.
- Partially observable environments, or POMDPs address problems of optimal exploration versus exploitation, where some of the actions might be information-gathering actions; whereas others might be goal-driven actions.
POMDP
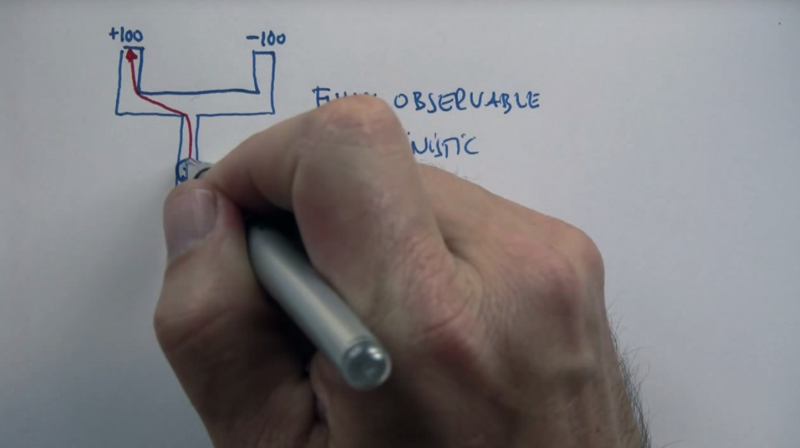
- When the world observable and the action is deterministic, Conventional planning will work and plan the best path to the goal state.
- When the world observable and the action is stochastic, MDP will work and find the best path to the goal state.
- When the world partially observable (e.g. we don’t know where the absorbing states are) and the action is stochastic, POMDP will need to gather information and then work to find the best path to the goal state.
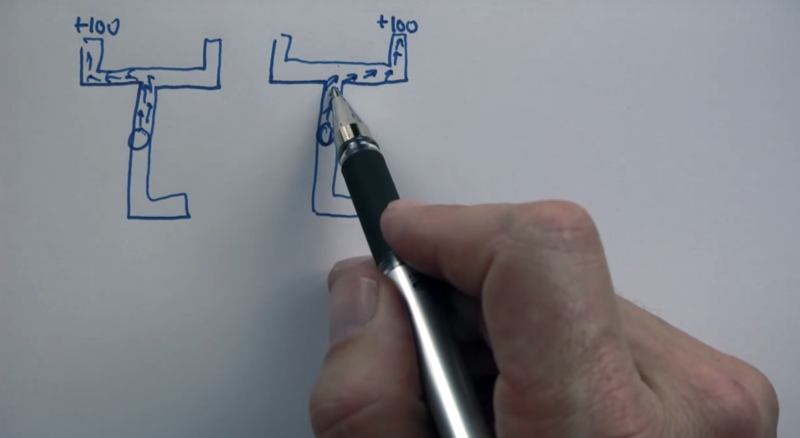
POMDP would not work when there are two worlds So here’s a solution that doesn’t work: Obviously, the agent might be in 2 different worlds and it does not know. Solving the problem for both of these cases and then put these solutions together will not work because the average result will never let it go south to gather information.
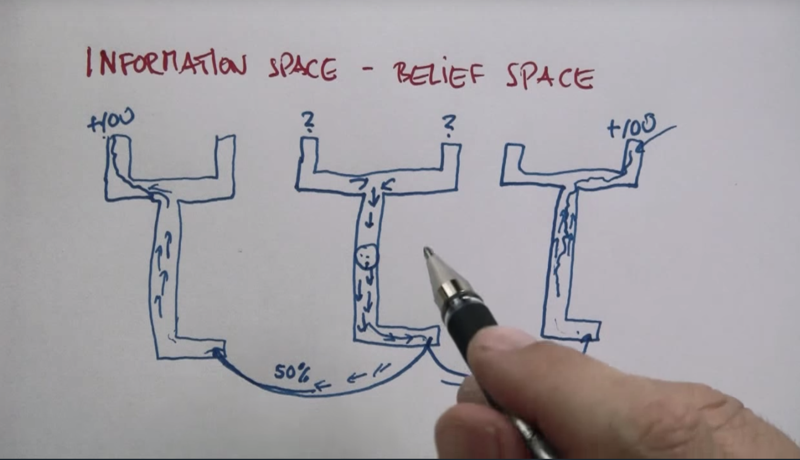
POMDP on belief states will work. If the agent goes south and reaches the sign. 50% chance it will go the right-side belief state. if MDP was performed, then it will reach the +100 state. the same will happen if it goes to left-side belief state (50% chance).
Readings on Planning under Uncertainty
AIMA: Chapter 17
Further Study
Charles Isbell and Michael Littmann’s ML course:
Peter Norvig and Sebastian Thrun’s AI course:
2018-12-01 First draft