Reinforcement Learning 第五周课程笔记

本周三件事：看课程视频 Convergence. 读 Littman and Szepesvari (1996), 作业四。

• no actions by learner. The value function is that value equals reward R(s) plus discounted expected value of the next state. (T(s, s’) is transision function.
• The new estimated value function for the state the learner just left is TD(0).

Q function is used to estimate the value at current state, take a action then get a reward and ended up in a new state < s_t-1, a_t-1,r_t,s_t >. The Q updating rule takes care of two approximations: 1) if model is known, it can be used to update Q; 2) if Q* is known, it can also be used to update Q.

And both will converge.

• See value iteration here

• Practically, if B is multiplying a number in [0,1), B is contraction mapping.

• take the first option for example:

  B(x) - B(y)

  =

  x/2 - y/2

  =1/2

  x - y

  , so there exists γ >=1/2 makes

  B(x) - B(y)

  <=γ

  x - y

  . So B(x) = x/2 is a contraction mapping.

• ① and ② are true, so that BF_t-1 = F_t, F_t will converge at F* through value iteration.

• If there is two fix point, G* and F*, Putting them into the B operator will not change the distance of them because both of them are fixed, and this violates the definition of B.

• Applying B operator to Bellman equation and unpacking

  BQ1 - BQ2

  ∞.

• Not combining the max a’ because the a’ are not the same in Q₁ and Q₂

• stop here, first, will go back. that’s call this the unfinished proof.

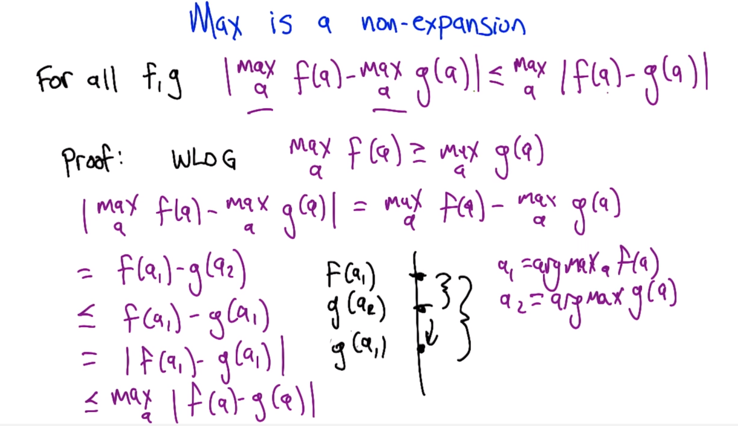
• Max is non-expansion:

  maxf(a) - maxg(a)

  <= max

  (f(a) -g(a)

  . Using this

The three properties need to be true for Q_t to converge to Q*. and they are true

So, Q-learning converges.

B_t is the operator we are going to update Q at t time step. Q(s,a) is the Q function value of the state we just left and Q function w is the Q value of the state we just arrive. In regular Q Learning update, Q and w are the same, here we separated them in the theorem.

So, rule number one is saying if we know the Q* and use the updating rule (in pink) to update the Q function, the expected value of the one-step look ahead (w) can be calculated and the stochasticity will be averaged out.

If we hold the Q(s,a) fixed and only varies the way we calculate the one-step look ahead, the distance between the Q* and Q can only get closer with each update.

The third condition is the learning rate condition. which is needed for Bellman equation.

• the take home messages are, these generalized MDPs all converges.
• so the correct answers are: (from top to bottom) worst possible decision, not-optimal decision, two agent competing decision making (the zero-sum game).

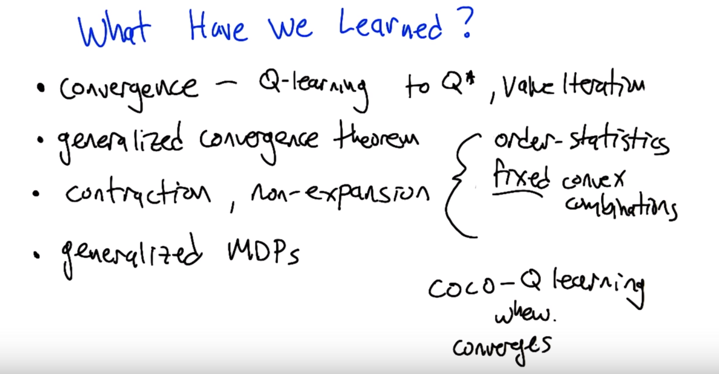
Generalized MDP can be seen as redefine fix point. Contraction might be something like “收敛” in Chinese. Q-learning converges to Q*. Generalized Convergence theorem uses two Q-functions to prove the convergence of Bellman Equation.