This week
- watch POMDPs.
- The reading is Littman (2009).

POMDP
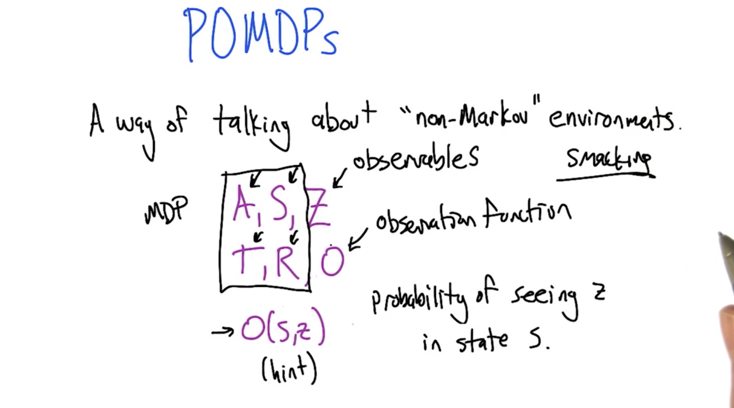
- POMDPs generalizes MDPs.
- In POMDP, MDP (represented by <S,A,T,R>) is not directly observable to the agent. we can only observe the states. Z are observables to the agent, Z is a set of states in S.
- O(S,Z) is the mapping function of Z to <S,A> (e.g. Given Z, what’s the probability of S).
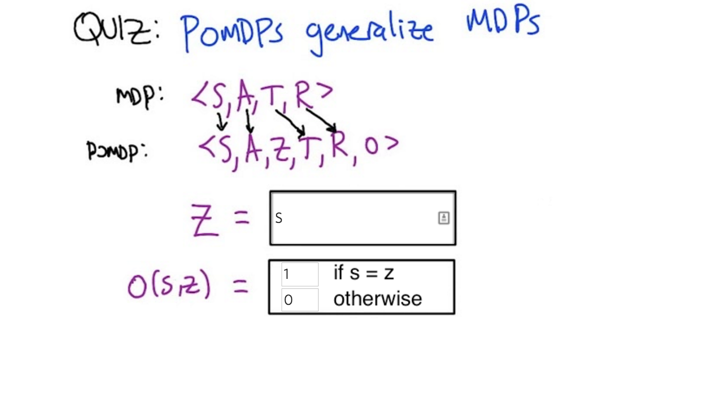
- When O(S,Z) = 1, the observable Z is S. So, Z and O together determines the relationship between S and Z in the POMDP.
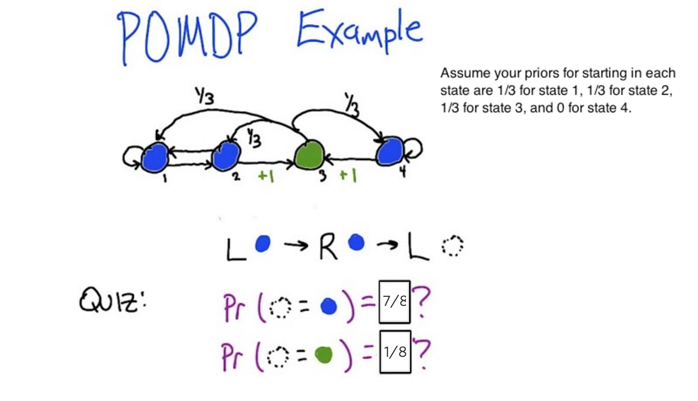
Solution:
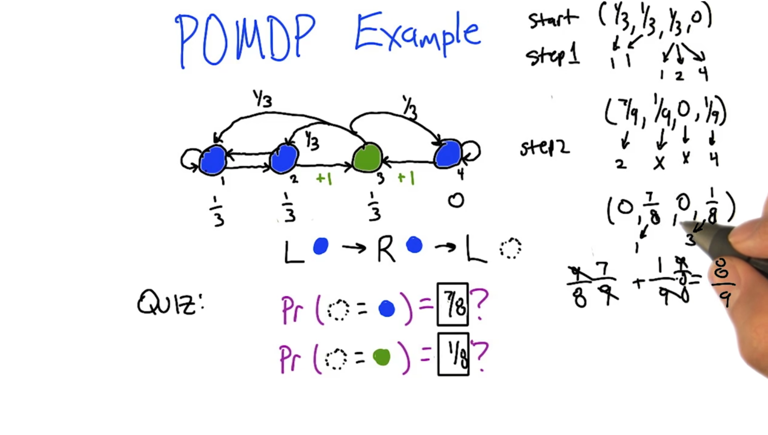
- keep track of probability of ending up in each state after each step.
- There is a normalization after each step (not the right thing to do but works.).
State Estimation

- Belief state b(s) is a probability distribution vector of whether we are in s.
- using belief state can turn POMDP into belief MDP <b, a, z, b’>
b’(s’) = Pr(s’ b, a, z) = Pr(z b,a,s’) Pr(s’ b,a) / Pr(z b,a) = Pr(z b,a,s’) sum Pr(s’ s,b,a) Pr(s b,a) / Pr(z b,a) = O(s’,z) sums T(s,a,s’) b(s) / Pr(z b,a) - Note: belief MDP has infinite number of belief states which make VI, LP, PI impossible because they can only deal with finite number of states.
## Value Iteration in POMDPs
Math
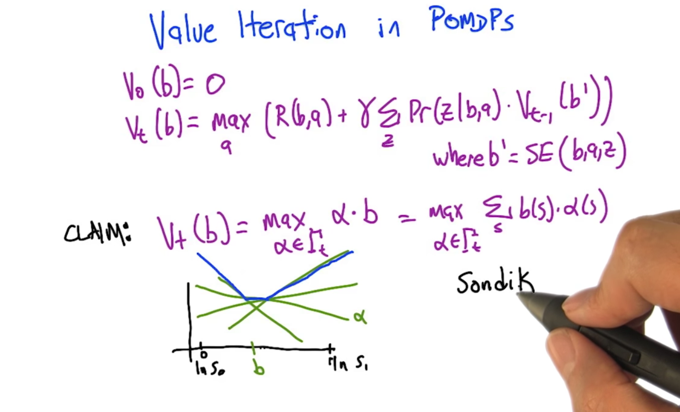
- Initialized V0(b) as 0
- Vt(b) can be written as something similar to bellman equation
- Claim Vt(b) can be represented by the maximum of a set of linear functions of b and α. α is a finite set of vectors. this is called piecewise linear and convex.
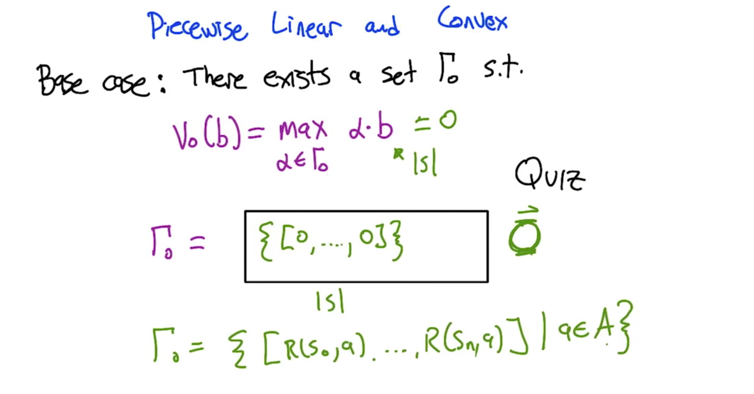
- Γ0 should be a vector of zeroes.
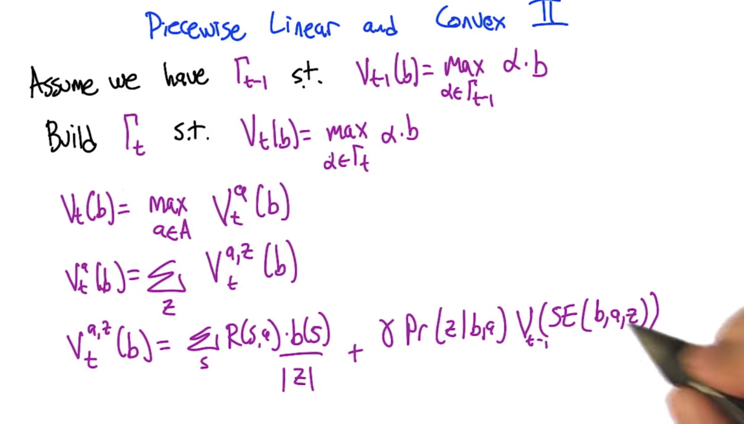
- Piecewise linear means Vt(b) can be represented by Vat(b), Vat(b) can be represented by Va,zt(b) and Va,zt(b) can be represented by something like a Bellman equation

- In a similar sense, Γt can be represented by Γat , Γa,zt and something like a Bellman equation.
- Thus the belief MDP becomes computable.
- pomdp-solve is an existing solver for pomdp.
-
Guaranteed to be exponential because size of Γ is exponential in respect to the size of observables: Γt = Γt-1 z </sup> dot A - the calculation could be faster if Q function (Vat(b) is the Q function) has a small representation.
algorithm
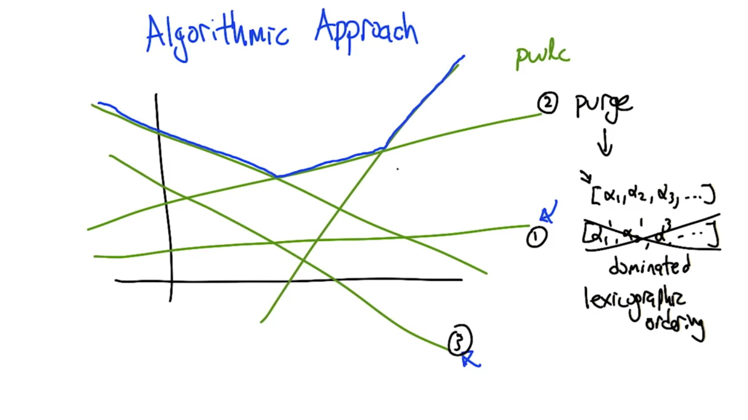
In the figure:
- all the linear functions (vectors) are dominated by the blue lines which involves three linear functions.
- function ① and ③ can be purged because they have no contribution to the overall vector
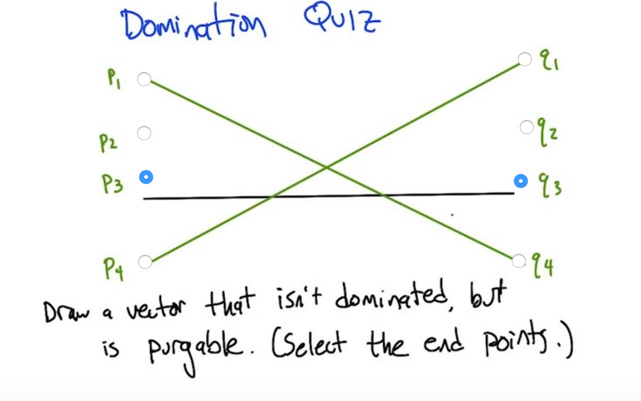
- Domination: if one vector is always less than (in this case) another vector, we say it’s dominated by that another vector.
- Vector is purgeable if it does not contribute to the max
Learning POMDP

- Planning: if know the model of POMDP, can run value iteration. Since POMDP have infinite number of states, we can only get approximation of optimal policy.
- VI may not be converge
- PI is not possible because infinite believe states
- Difference between planning and reinforcement learning:
- Planning: know the model - planning in POMDP is undecidable.
- RL: we don’t know the model have to interact to learn
- RL has 2 types:
- Model based RL: learn the model (POMDP) and use it
- Model free RL: don’t learn the model but mapping observables and action.
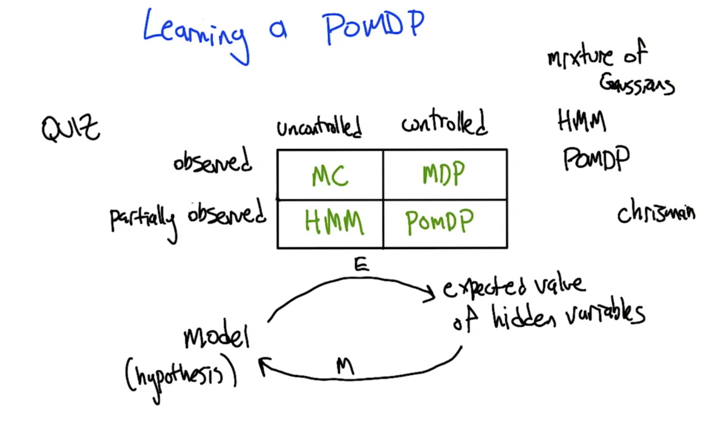
- MC: Markov Chain, observed but uncontrolled; HMM: Hidden Markov Model, partially observed and uncontrolled; MDP: observed and controlled. POMDP: partially observed and controlled.
- EM: Expectation Maximization, an procedure to learn the hidden property in HMM or POMDP.
- Model based Learning.
## Learning Memoryless Policies (Model free RL of POMDP)
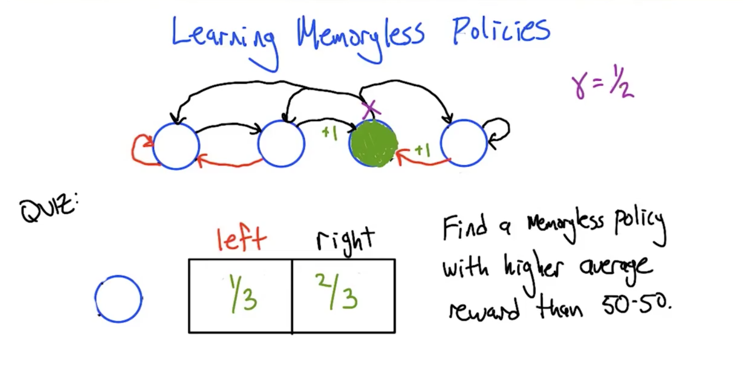
- in the MDP, There 3 blue states, to get to the green state, the agent needs to move to right in 2 of the states and move to left in another state. So the solution for this quiz is 1/3 and 2/3.
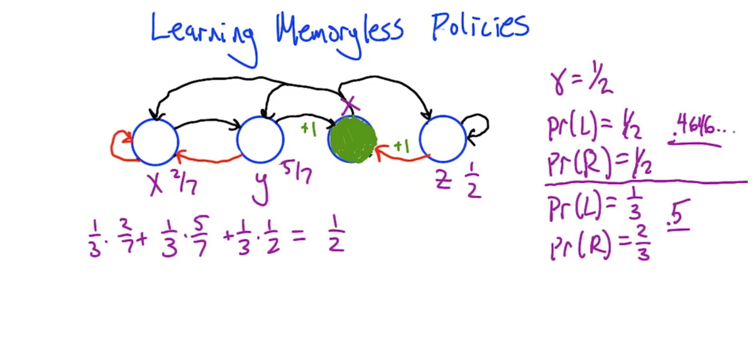
- solve and compare the value function based on the 50-50 probability (policy) and 1/3 - 2/3 policy.
X = p * (0.5 * X) + (1 -p)(0.5 * Y) => X = 0.5 * (1 - p)Y / (1 - 0.5p) Y = p * (0.5 * x) + (1 -p) => X = 2 *(Y - 1 + p) / p Z = p * (1) + (1 -p) (0.5 * Z) => V = 1/3 * (X + Y + Z)
RL as POMDP:
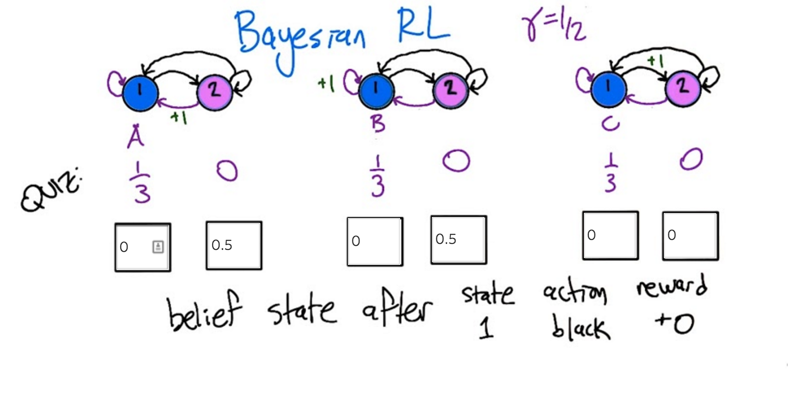
- we can be in MDP A or B but not C, and we will be in state 2.
- Next, we can take a purple action to figure out which MDP we are in.
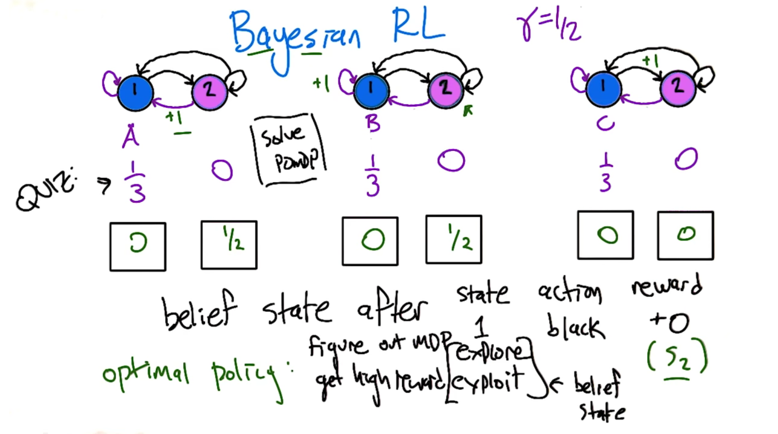
- So the optimal policy is figuring out which MDP we are in and get hight reward by exploiting in the belief state.
- RL itself is like POMDP which requires exploring and exploiting.

Predictive State Representation

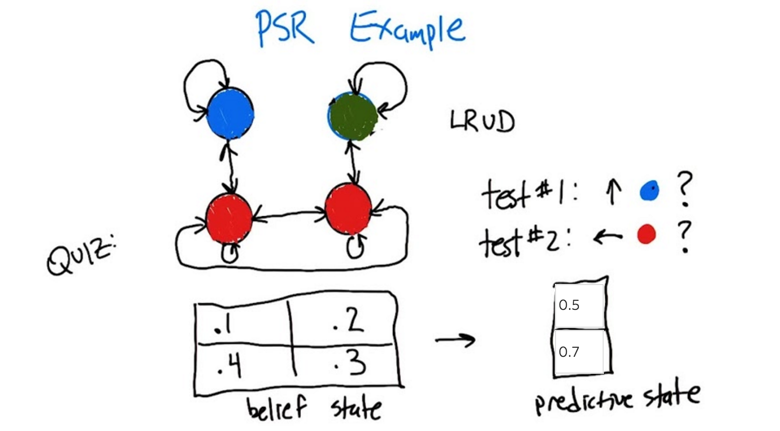
- The POMDP has 4 states but 3 observables represented by colors where the two red states are not distinguishable.
- We can do test to get predictions of states. (e.g, a test can be moving up, and see the probability of ending up at the blue test).
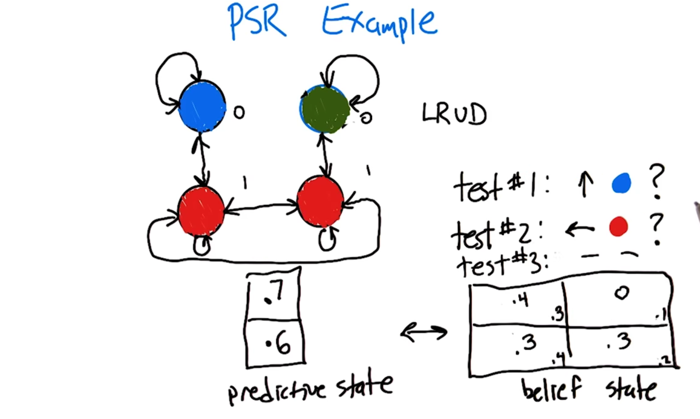
- Belief state and predictive state does not have a one-on-one mapping.
- Increasing number of tests will constrain the mapping.

Why go to PSR?
- We can not observe all the states in POMDP and they might not even exist.
- we can do some test to figure out what state we might be in.
- Learning a PSR sometimes is easier than learning a POMDP.
- Number of test is always going to be no more than the number of states

2015-10-23 初稿
2015-11-03 补全
2015-12-04 reviewed