This week
- watch Game Theory.
- The readings are Littman (1994), Littman and Stone (2003), Greenwald and Hall (2003), Munoz de Cote and Littman (2008).
- Assignment 10 is up.

- Game theory is mathematics of conflict of interests.
- It generalizes the RL from single agent to multiple agents.
- It is of the interest of economics, politics, sociology or even biology since these fields often deal with agents with many many agents with conflicts of interests.
Example

- The example game is represented as a tree, nodes are states, edges are transitions and leafs are rewards.
- the example game has 2 agent (a and b), all the rewards added up to be a constant ( zero-sum), no stochastic transitions. The leafs show the reward that agent a can get and b gets (-1 * reward).
- Strategies: what action should the agent take at each state it could be in. (equivalent to policy in RL)
- The agents are assumed to be rational.
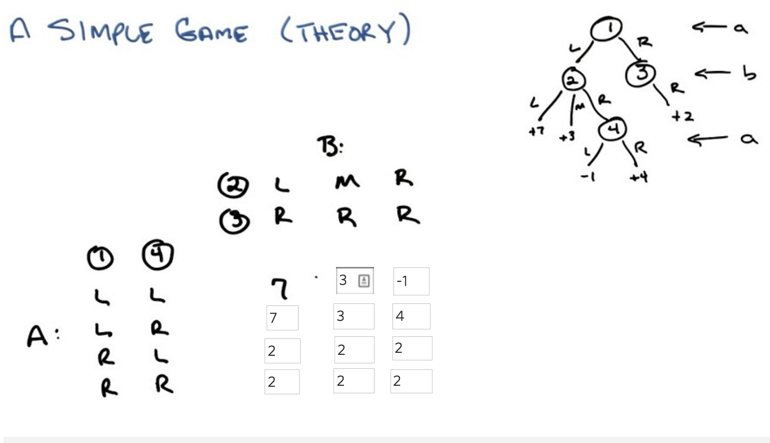
- this is a simple example of 2-agent zero-sum game
- zero-sum means the reward of A and B will sum to 0 for any strategy.
- A matrix is enough to represent a game.
- once the matrix is here, the tree doesn’t matter now.
- need to learn to generate the matrix from the tree.
Minimax

- A and B has the same goal, maximize their own reward ( and minimize others reward).
- If A and B behave rationally, they will reach the same strategy.

This is important so I am writing it down:
- In a 2-agent, zero-sum, deterministic game of perfect information, Minimax ≡ Maximin,
- and there always exist an optimal pure strategy for each agent.
- Based on the strategy matrix, one can always build at least one tree.
Now, to make the problem a bit more complex, we change the game to be non-deterministic:
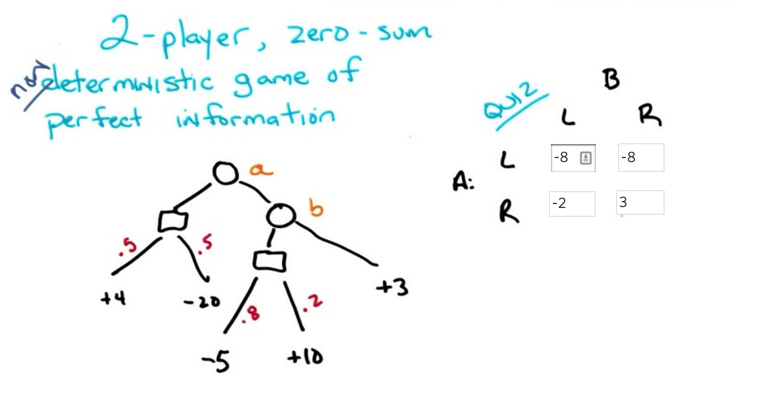
- Introduce the chance box, so that transition is non-deterministic.
- construct the strategy matrix based on tree ( but could not reconstruct tree based on matrix)
- note: from the matrix, we don’t know if the tree is deterministic or not.
- the minimax theorem (Von Neumann theorem) still holds
- Minimax ≡ Maximin
- Optimal pure strategy exists.
Minipoker

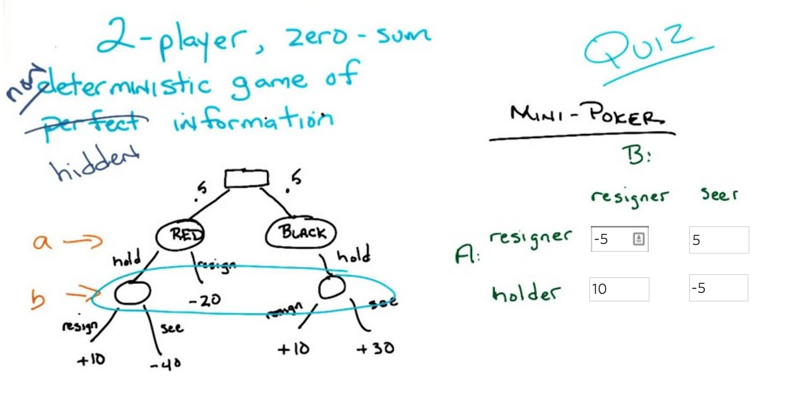
- In the minipoker game, b will not know all the information, so it’s a 2-agent, zero-sum, non-deterministic game of hidden information
- In this case, Minimax ≠ Maximin and there will be no optimal pure strategy.
- but there will be mixed Strategy, which is a distribution of strategies.
Mixed Strategy

- A’s expected strategy are linear equation, which can be represented by lines.
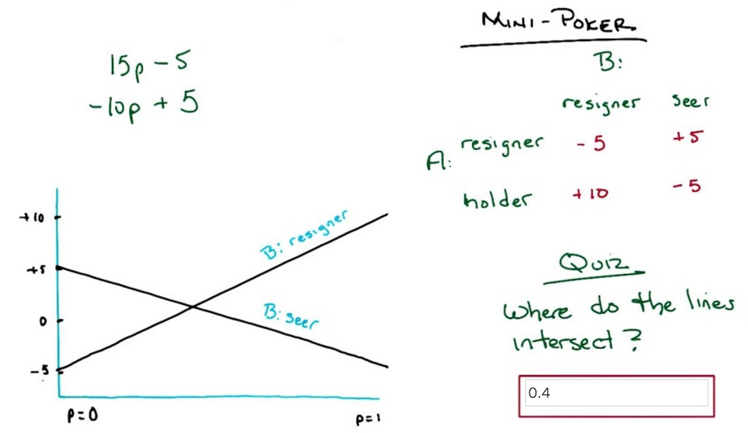
- the mixed strategy should be at the intercept of the two lines in this case.
- if the two lines both have positive slope, the mixed strategy should be at the far right; if negative slope, the strategy should be at the far left.
- the expected value of the game is deterministic still.
- although the strategy is mixed, there is still an expected value, in this case, the expected value is when p is 0.4, and value is 1.
Snitch
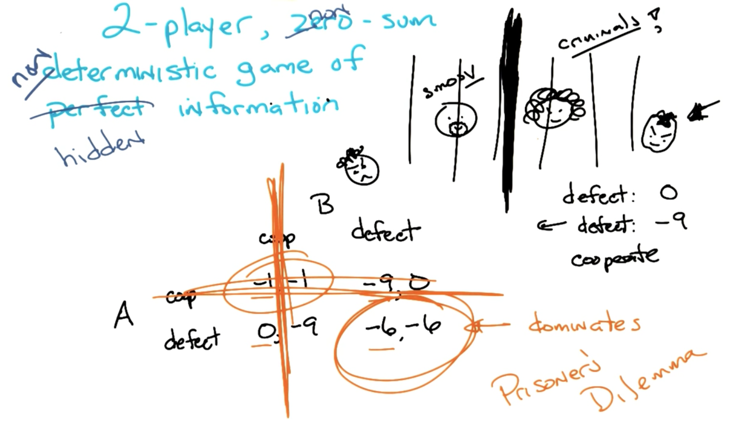
- Now, we are making the game non-zero-sum.
- The prisoner’s dilemma is a 2-agent, non-zero-sum, non-deterministic game of hidden information
- Assume the agents are rational, both of them should defect.
A Beautiful Equilibrium

- in practice, if we are in a Nash Equilibrium, any agent will have no good reason to change strategy ( pure or mixed).

- in the n-player pure strategy game, if elimination of strictly dominated strategies eliminates all but one combination, that combination is the unique NE.
- Any N.E. will survive elimination of strictly dominated strategies
- if n is finite, for each set of finite strategies, then there will be at least one strategy is N.E.
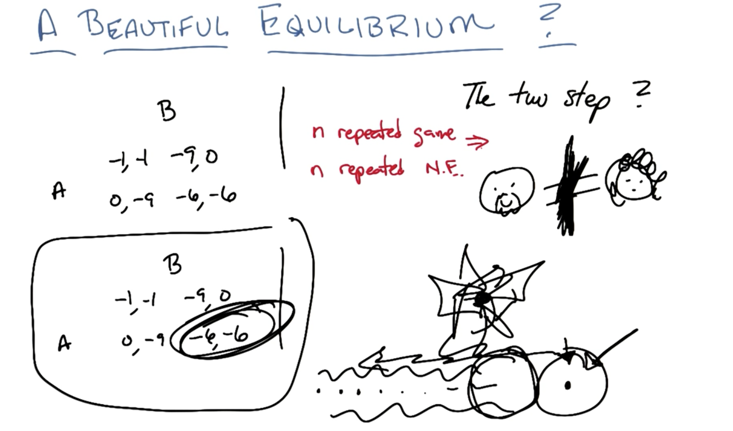
- what if playing the game multiple times?
- only the last game matters-> the last game will be N.E -> since the last game is known now, the last game moves to the game before it.-> the last game will be N.E. -> repeat…. ->all the game should will be N.E.
Recap
Andrew Moore’s slides on Zero-Sum Games Andrew Moore’s slides on Non-Zero-Sum Games
2015-11-03 初稿
2016-04-26 复习并添加部分内容