Reinforcement Learning 第十四周课程笔记

• Inverse Reinforcement Learning
• Policy Shaping
• Drama Management
• what have we learned

This week 

• should watch CCC.
• The readings are: Zeibart et al. (2008). Babes et al. (2011). Griffith et al (2013). Cederborg et al (2015). Roberts (2006). Bhat (2007).

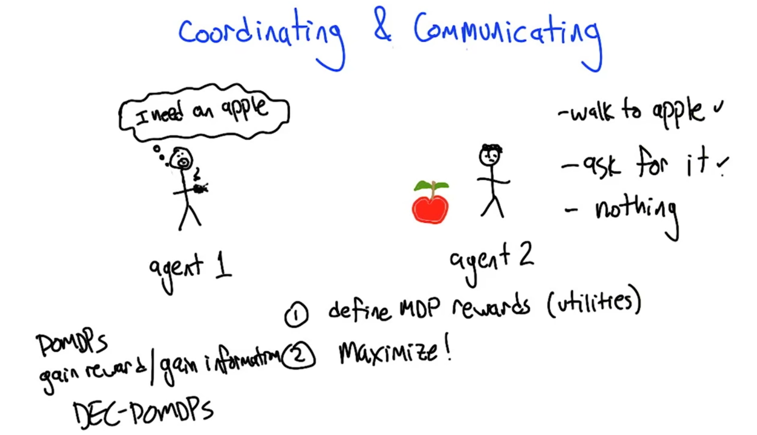
• Dec-POMDP has some perspectives of game theory and MDP
• Multiple agent working on getting a common reward. (if the rewards are separated for all the agents, then it’s a POSG partially observable stochastic game)

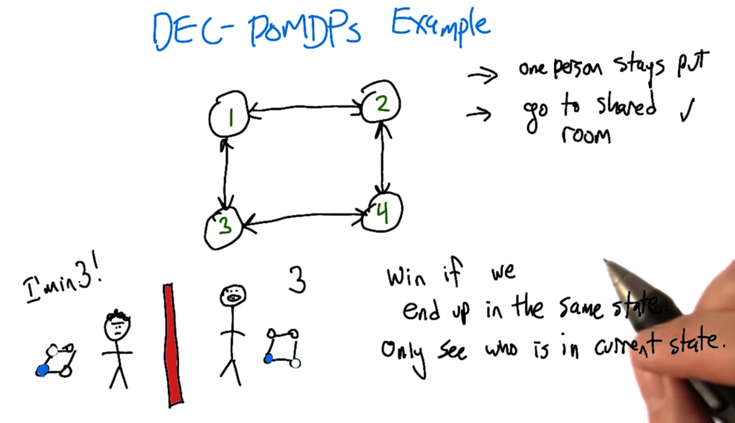
• two agents, they know where they are but don’t know the other’s position. when the two are in the same room, they win.
• Strategy: go to a shared room. But my knowledge of my current position could be wrong ( partially observable world).

• agent 1 wants to set up some kind of reward function to move agent to do something (e.g. get the apple for me).

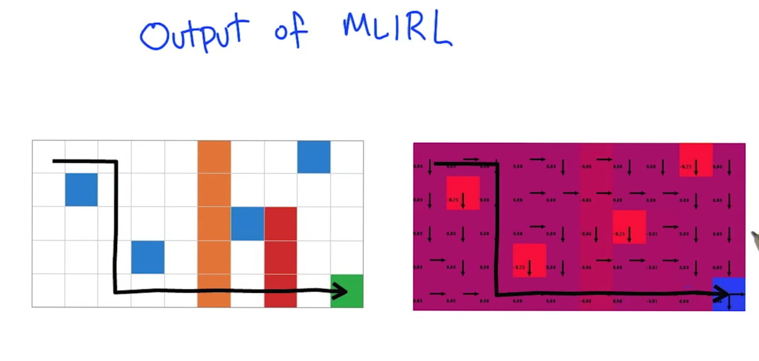
Inverse Reinforcement Learning

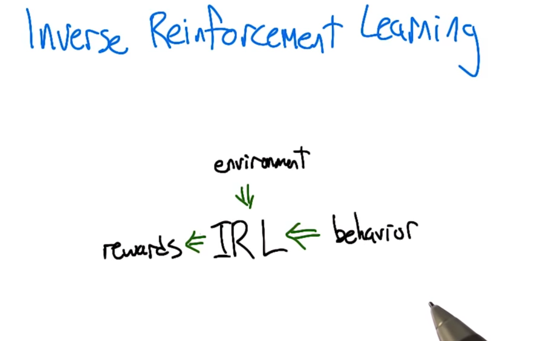
• Inverse Reinforcement Learning: the agent experience the environment and a set a behavior and then generate a reward function based on the inputs.

Policy Shaping

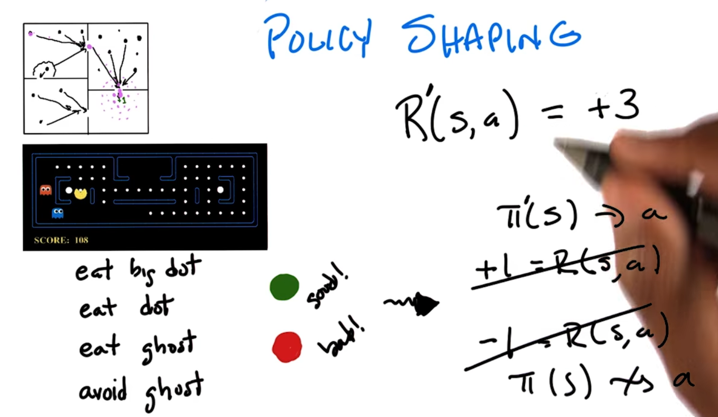
• if a human is giving feedback (commentary) about weather the agent’s action is good or bad, s/he is doing policy shaping.
• policy shaping could be realized by reward shaping which is replace reward of an action with a new reward?
• Agent need a mechanism to learn from the environment and the commentary to decide what policy to take (not just listening to the commentary, cause the commentary might not be always right).

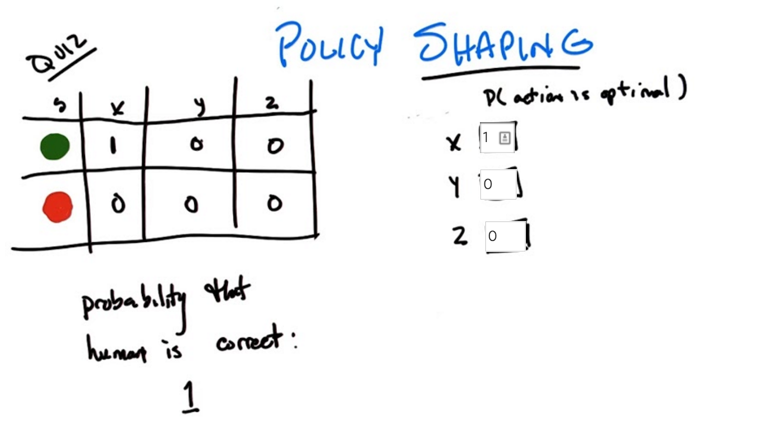
• If human is alway correct, given the feedback, what’s the probability that the action (x, y, or z) is optimal?
• answers in the slides above.

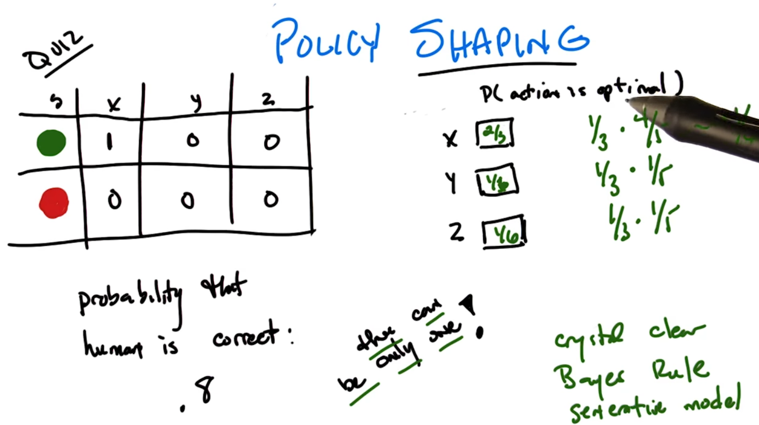
• what if human is 0.8 probability of right?
• counting method:
  • saying x is optimal is liking saying y and z is not optimal.
  • since human is 0.8 correct, then x, y, z being optimal is 0.8, 0.2, 0.2.
  • normalize the numbers above, will get 2/3, 1/6, 1/6.

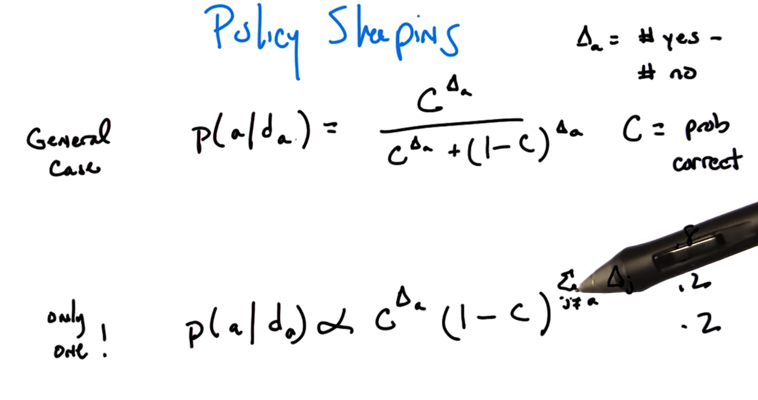
• Δ_a is coming from data of action a (d_a). C is the probability of correct of the people giving commentary.
• The formula above give the method of calculating probability of action a is optimal.
• Note: the final probability will need to be normalized against the probabilities of other actions.

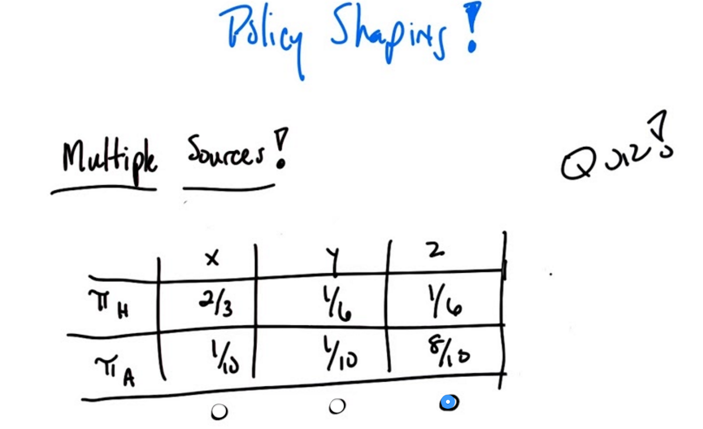
• in the policy shaping case, information are coming from multiple sources.
• E.g. π_a and π_H are policy info from agent exploring the world and human giving feedback.
• Some algorithm decrease the importance of π_H as time goes. One need to know that π_a already incorporated the information of human uncertainty (C).

• the way to combine the two sources is to calculate the probability that the two policy will agree: aopt=argmaxa p(a

  π1) * p(a

  π2).

  • in the quiz x_opt = 1/15, y_opt=1/60,a_opt=2/15. So we should choose z as optimal.

Drama Management

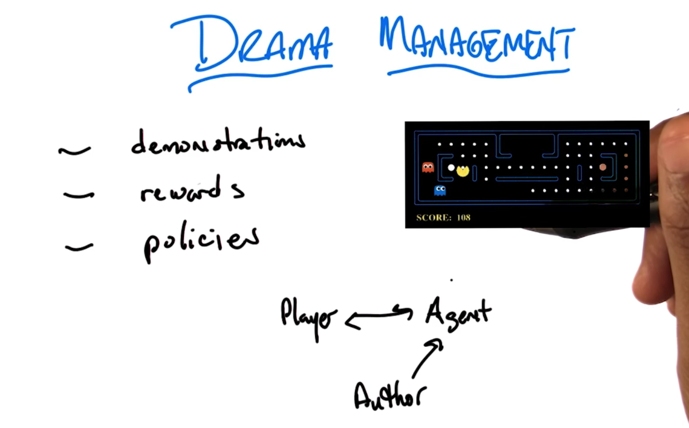
• the way a human can communicate to an agent
  • demonstration: show the agent what’s the correct action (inverse RL)
  • reward shaping: giving reward for agent’s actions
  • policy shaping: commentary on the agent’s actions
• author convey his intent to the agent so the agent can

• story can be defined as a trajectory through plot points

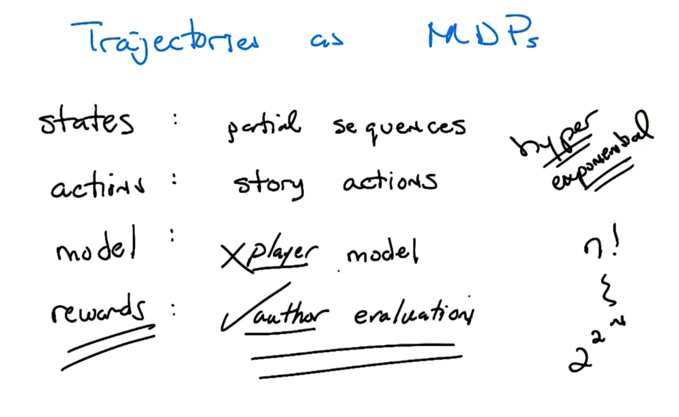
• above a some mapping of MDP elements to trajectory MDP elements
• Problems
  • large number of sequence of states (hyper exponential)
  • Since MDP will maximize rewards, treating story as an MDP will only make the author happy and force the player to experience the story.

• p(t’	a,t) is the probability that the player at trajectory t and take action a then ended up in trajectory t’. P(T) is a target distribution.

• the action is not player’s action but the story action
• the optimal policy is the policy that will lead to the targeted trajectory distribution P(T)
• the calculation time is linear and dependent on the length of the story.

what have we learned

2015-11-18 初稿 完成