Machine Learning笔记 第02周

• SL4: Instance Based Learning
• SL5: Ensemble Learning Boosting

本学期学习Machine Learning。本课程在Udacity上有免费版本，并提供详细的笔记。本文的笔记是超级脱水版，目的是自用。

Week 02 tasks： * Lectures: Instance Based Learning, Ensemble B&B, and Kernel Methods & SVMS.

• Readings: Mitchel Chapter 8, Schapire’s overview to Machine learning and Jiri Matas’ slides on AdaBoost.

SL4: Instance Based Learning

• Lesson 4 Notes
• Instance Based Learning

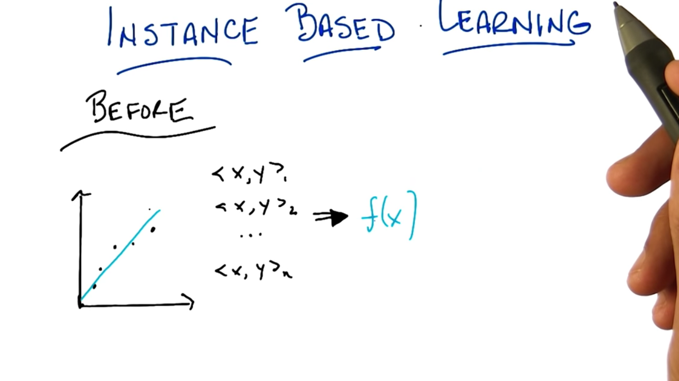
• in supervised learning, we learn a function from data and use the function to predict future data.

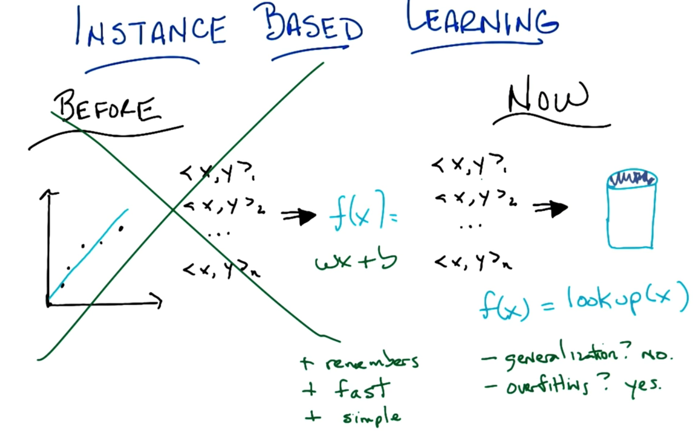
• Now we keep everything in a database and f(x)=lookup(x). this database approach has pros (fast and simple) and cons (no generalizable and overfitting).

• classify unknow price houses by
  • nearest neighbor
  • k nearest neighbors

• in K-NN, there are a lot decisions can be made to get the result: e.g. classification: by voting or weighted voting; regression: average or weighted average.

• the running time and space required for each algorithm.
• Sorted data points is more efficient in query.
• Lazy learning (push work to when it’s needed) V.S. eager learning

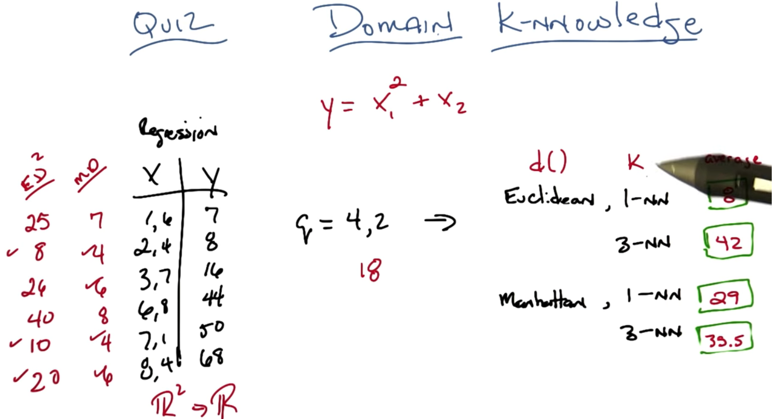
• Different distance function and K makes very different prediction of the query point q.

• K-NN works well when data has 1) locality, 2) smoothness and 3) equality of features

• This is bad
• the curse is not just for KNN, it’s for ML.

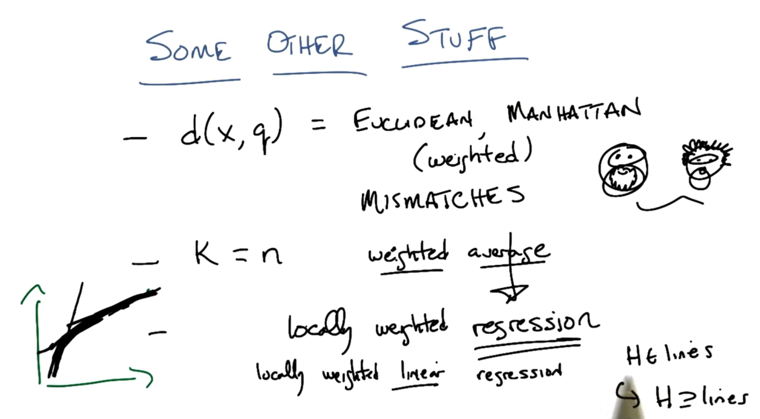
• Picking d(), picking K, replacing average with local weighted regression.

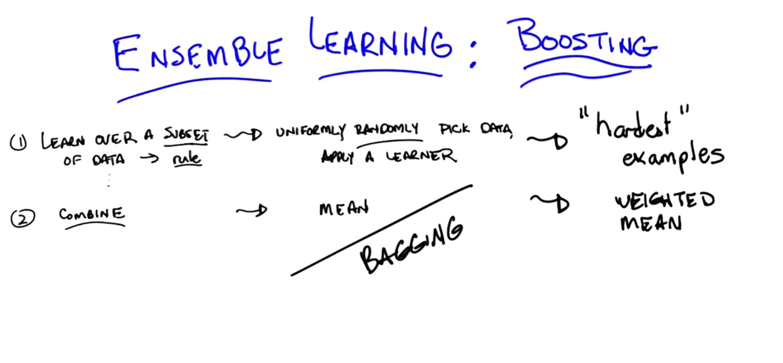
SL5: Ensemble Learning Boosting

• Lesson 05 Notes
• Intro to Boosting

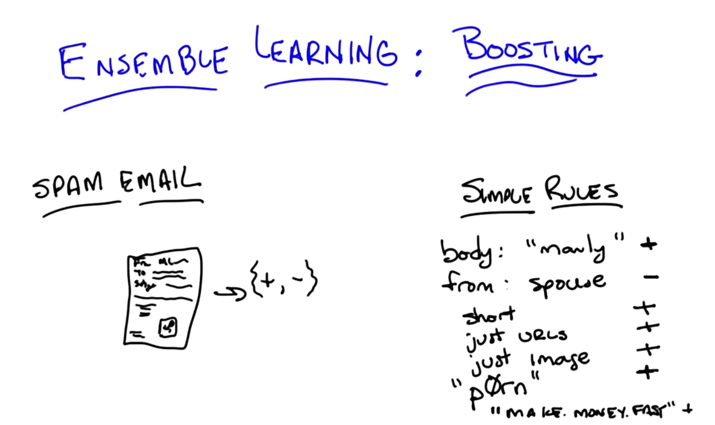
• example of spam email rules: but the rules are not definitive.

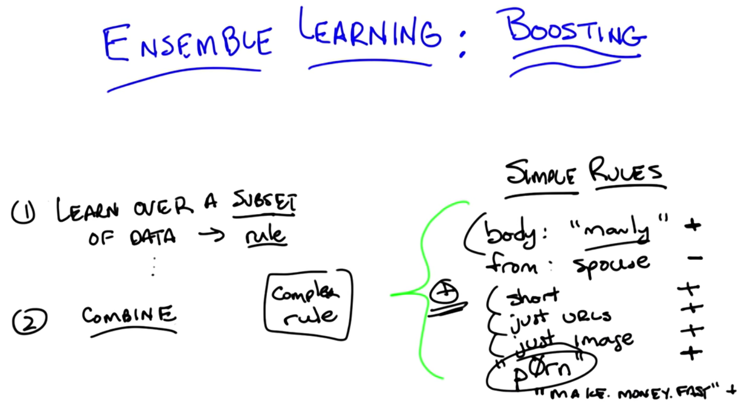
algorithm:

1. pick up rules from subset of training data and
2. combine rules.

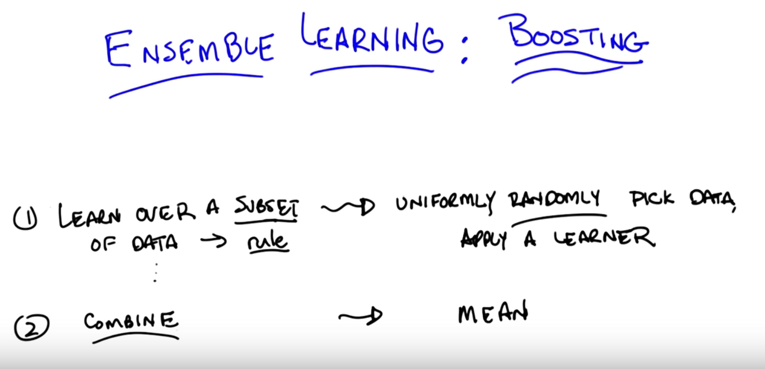
For each step of ensemble learning algorithm, there are multiple ways of doing things.

• picking up dataset uniformly randomly and
• combine by average give us bagging. See examples below.

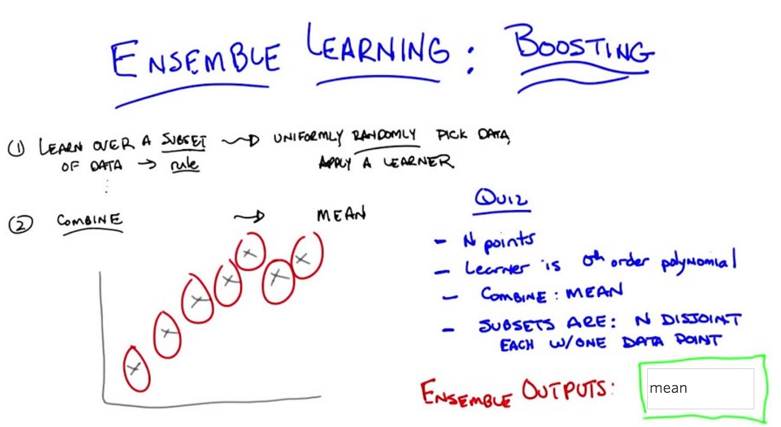
Example 1:

• N points and learner is zeor order polynormial
• combining method: mean
• Subsets are N disjoint, each w/ one data point.

What’s the ensemble output? A: average of N data points.

Now, another example:

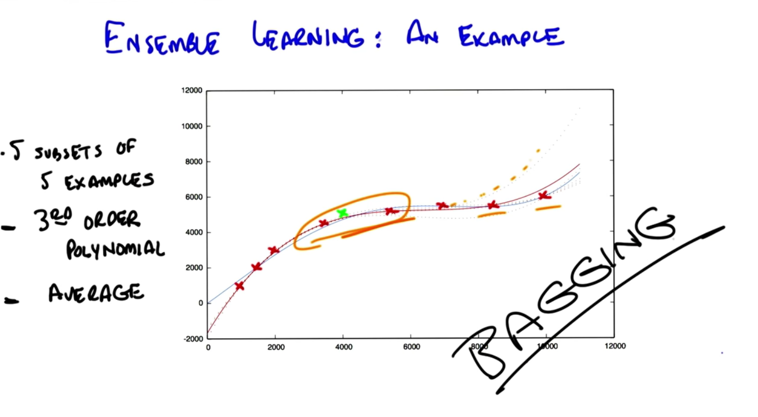
• 3rd order polynomial (redline) on subset is better than 4th order polynomial on whole data on testing. It somehow removes overfitting.
• Bagging or bootstrapping: take a random subset and combine by the mean

New subsetting and combination method:

• Choose hard examples: hard relative to if we were to stop now, how well we do?
  • hard samples are samples which hypotheis do not match with the target function
• Use weighted average

• subscript D stands for distribution. So h is the hypothesis and C is the true underlying concept.
• Olde definition: an error rate or an error percentage as the total number of mismatches over the total number of examples
• New Definition: error is the probability, given the underlying distribution, that I will disagree with the true concept on some particular instance X.
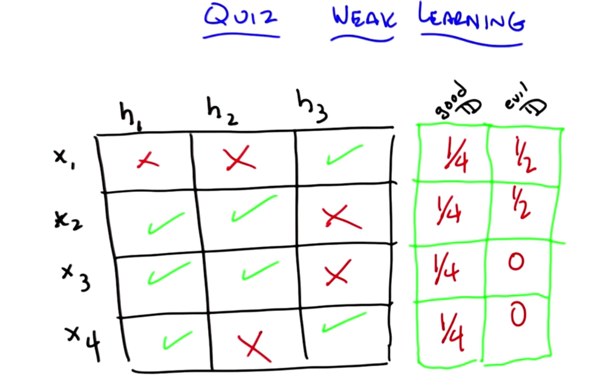
• Quiz 2: say we have 4 instance, we got 2 correct and 2 wrong, what’s the error? A: 0.5, assuming each instance has the same possibility to be seen.

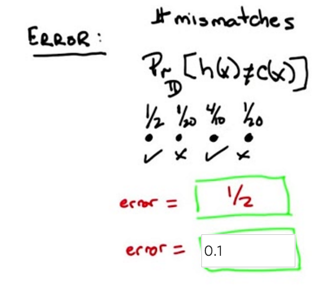
• What’s the error rate using new definition? A: 0.1.

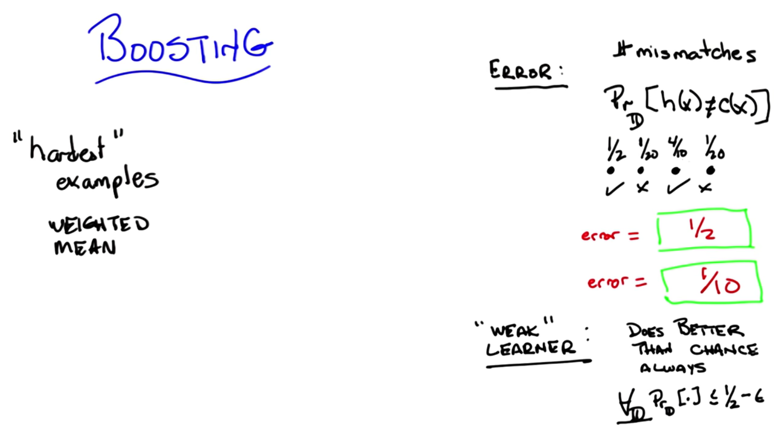
• a weak learner is a learner that, no matter what the distribution is over your data, will do better than chance when it tries to learn labels on that data.

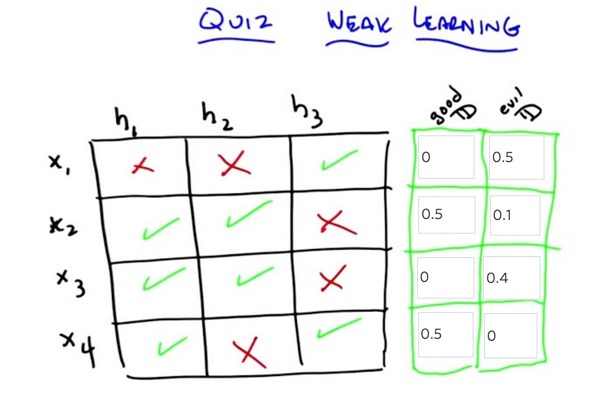
• Good D: find distribution over the 4 different examples, such that a learning algorithm that has to choose between one of those hypotheses will in fact be able to find one that does better than chance (by having an expected error less than 1/2)

• evil D: find a distribution such that if you have that distribution over the four examples, a learning algorithm that only looked at H1, H2 and H3 would not be able to return one of them that has an expected error less than 1/2.

• a training set made up of a bunch of x_i, y_i pairs.
• loop at every time step t, from step 1, to some T
  • construct a distribution D_t
  • Given that distribution, find a weak classifier to output hypothesis H_t with some small error  ϵ_t, and ϵ_t can’t be bigger than 1/2.
• eventually, output some final hypothesis. H_final.
• the two really important things are left out:
  1. where do we get this distribution and
  2. where do we get this final hypothesis?

• Important part 1: how to construct distributions
  • initial D(i) = 1/n. No special weights
  • for D_t(i), use normalized (by Z_t) distribution which is weighted by e to the alpha, Y, and h_t .
• When y and h_t disagree, the distribution will change. but whether the change is increase or decrease will depends on normalization factor and others.

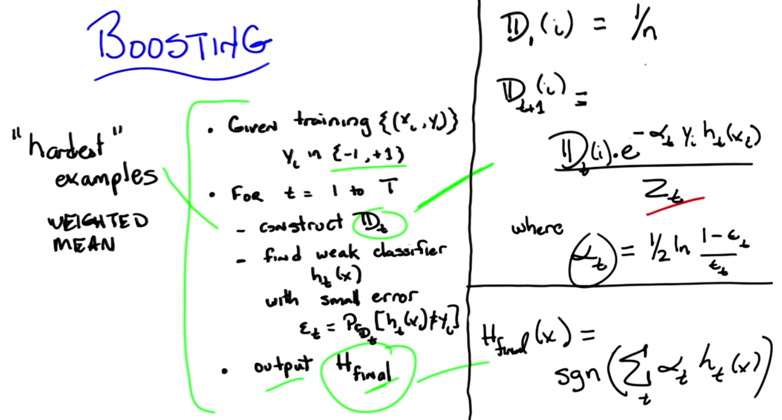
• H_final is defined as a SGN function of the sum of all the weighted hypothesis.

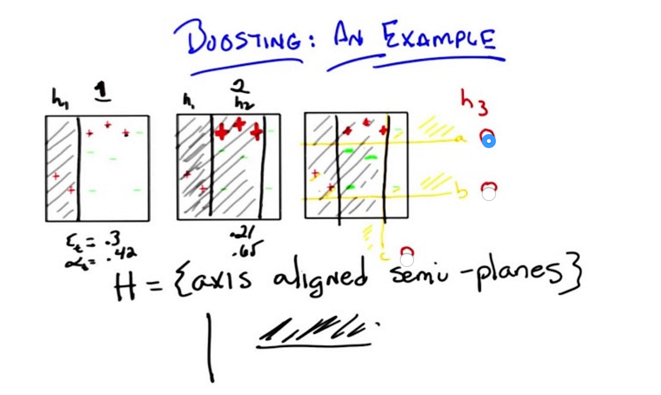
• in three steps, boosting will solve the problem of separating red positive sign and green negative sign.
• Size of sign represents their weights.

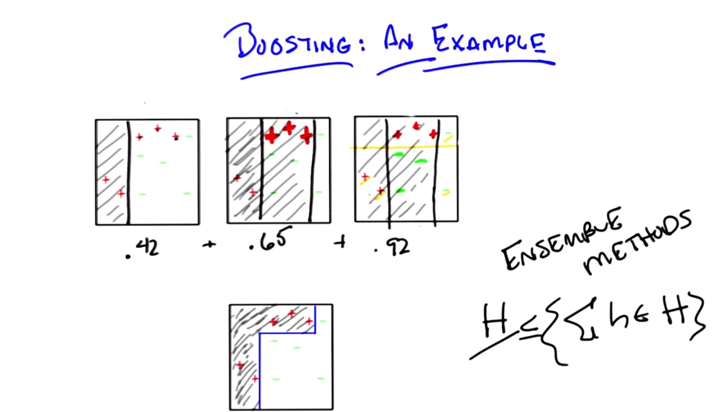
• by average the three hypothesis, we can get the correct Hypothesis here.

I am lost here, and need to read the proof!

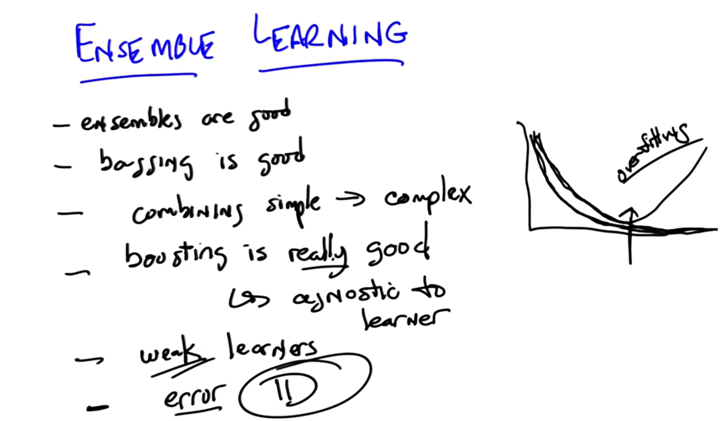
In practice, Boosting might not have a overfitting problem (testing error goes high)

2016-01-24 SL4 完成
2016-21-25 SL5，初稿完成