Machine Learning笔记 第03周

• SL6: Kernel Methods and SVMs
• SL7: Computational Learning Theory

Week 03 tasks：

• Lectures: Kernel Methods & SVMs as well as Computational Learning Theory.
• Reading: the tutorials on SVMs, as well as the relevant portions of Mitchell Chapter 7 for Comp. Learning Theory.

SL6: Kernel Methods and SVMs

• Lesson 6 Notes
• Kernel Methods and SVMs

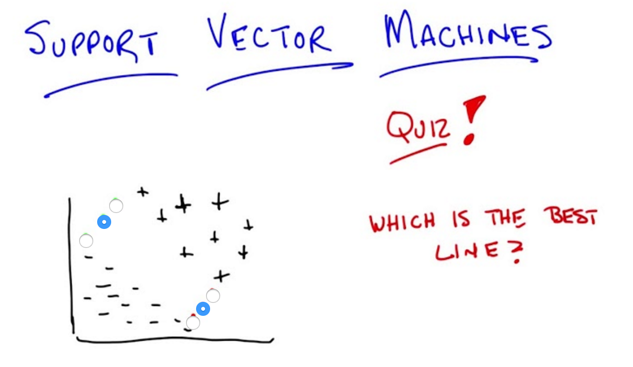
• the middle line is consistent with the data but least commitmented to the data ( to avoid overfitting)

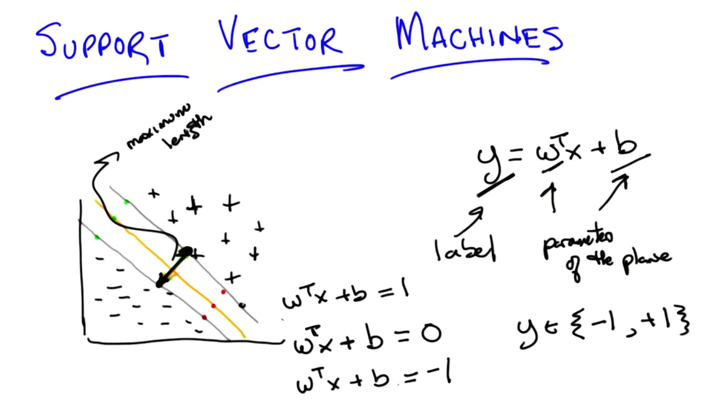
• y is classification label, and the boundary line (orange line) and negative and positive plane is defined.
• We should maximize the vector between the two grey lines.

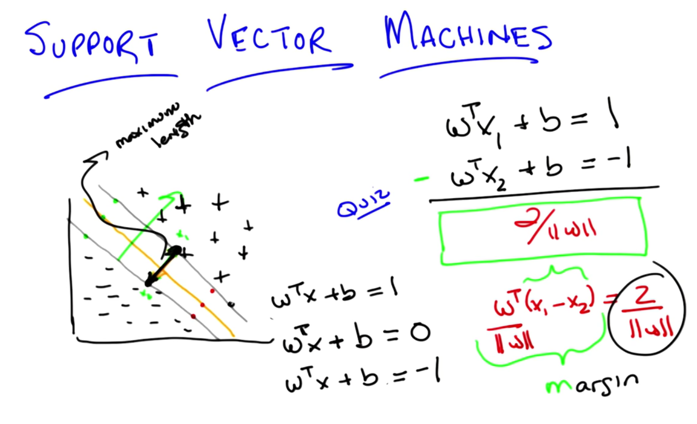
• This finding the best line (least commitment line that separates the data) problem it actually maximizing the margin (2/

  w

  )

• maximizing the margin problem can be converted to minimizing 1/2 *

  w

  2, which is a quadratic programming problem.

• it can be further expressed as another quadratic programming problem W(α)

• w is the sum of the product of α_i, y_i and x_i
• for the most of time, α_i is 0.
• quiz: in the graph in the right-bottom corner, which point is most likely to have an α_i == 0?
  • answer: the points that are faraway from the optimal separator (or decision boundary) doesn’t matter.
  • It’s like KNN but you already figured out which points actually matter by quadratic program
• x_i^T x_j is a measure of how similar x_i and x_j are.

###

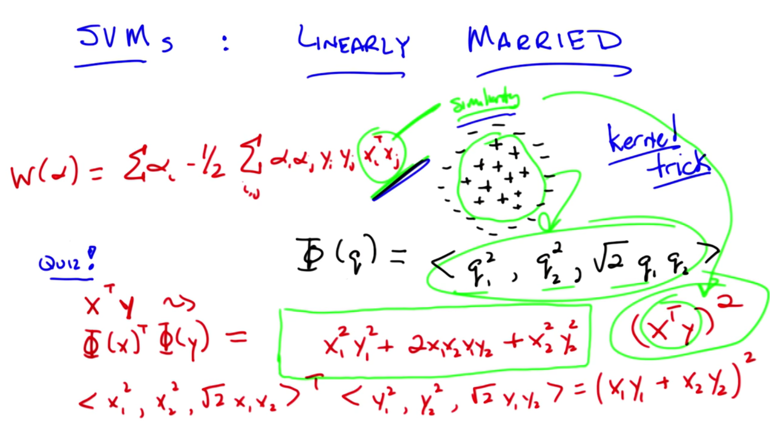
• for the pluses surrounded by minuses, they are not linear separable.
• by introducing an function with a three dimensional tuple, we can separate them in a higher dimension.
• the new function is equivalent to take the squared value of x_i^T x_j
• with more complicated data, higher dimension can be used. this is called the Kernel trick. the kernel function can be expressed by k(x_i, x_j)
• Kernel captures the domain knowledge

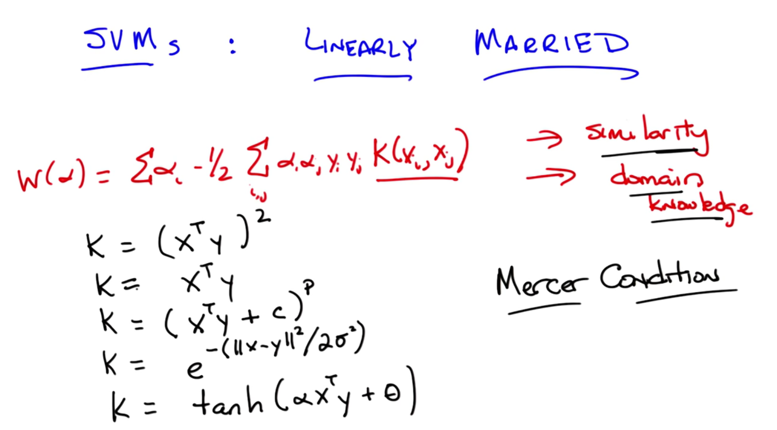
• radial basis kernel
• sigmoid-like kernel
• Mercer Condition: it acts like a distance, or a similarity

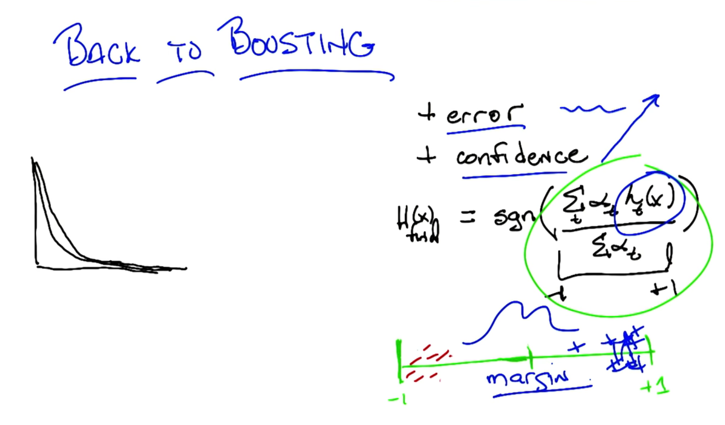
• First, we normalize the final hypothesis with Σα_t.
• With each loop of boosting, the items that were hard to separate got separated further, e.g. pushing negative to the left and positive signs to the right.
• Without changing the error, booting makes the margin larger and larger, thus it more likely to avoid overfitting.
• But Boosting could be overfitting in practice

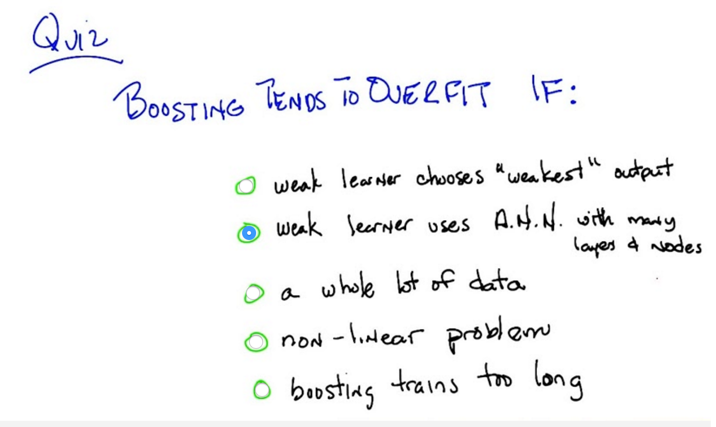
• explanation: if using a complex ANN, applying the training might end up no error, and the distribution will not change at all for the next loop. So no matter how many loops boosting goes through, it will end up of only one hypothesis which is the ANN. ANN overfits so that Boosting overfits.
• pink noise, a.k.a uniform noise, also tends to cause boosting to overfit. (by the way, white noise is gaussian noise).

SL7: Computational Learning Theory

• Lesson 7 Notes
• PAC Learning

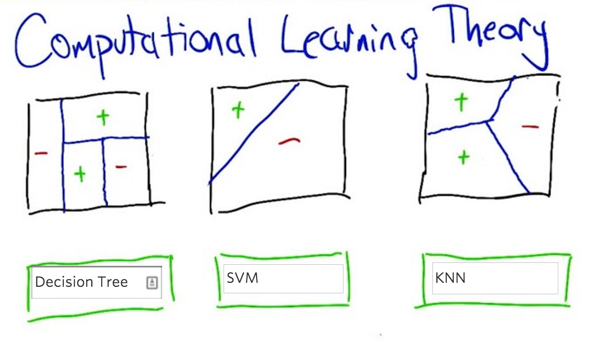
• First, decision tree
• second, SVM, or Perceptron or neural network
• Third: K-NN, k =1.

• my answer was: space, time, training set, testing set

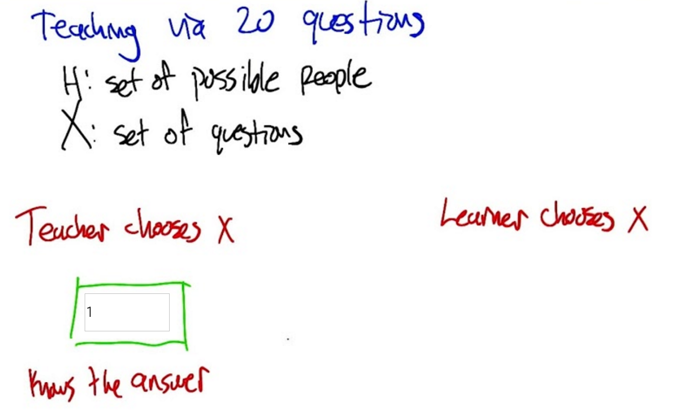
• If the teacher (who knows the answer) tells learning to ask X, then learner ask the question. the learner can get the answer in 1 step.

• if learner ask questions, how many steps s/he needs to get the correct answer? log2

  H

• Answer: we want to choose a question that can eliminate half of the information at each step. And the number of times you can divide a number in half before you get down to one is exactly the log₂.

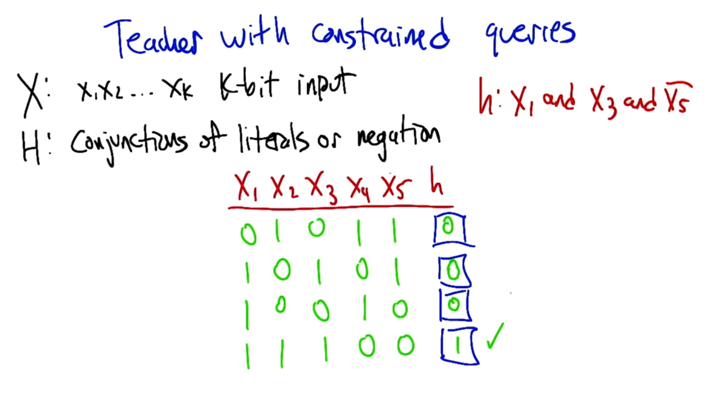
• teacher is constrained because only information of X1, X3 and X5 will be considered

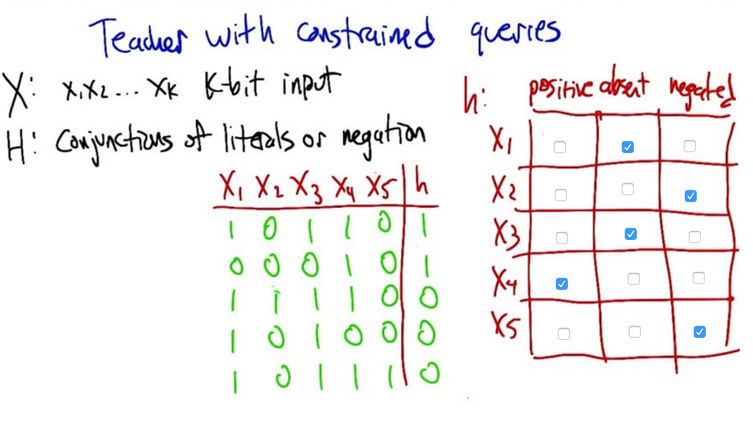
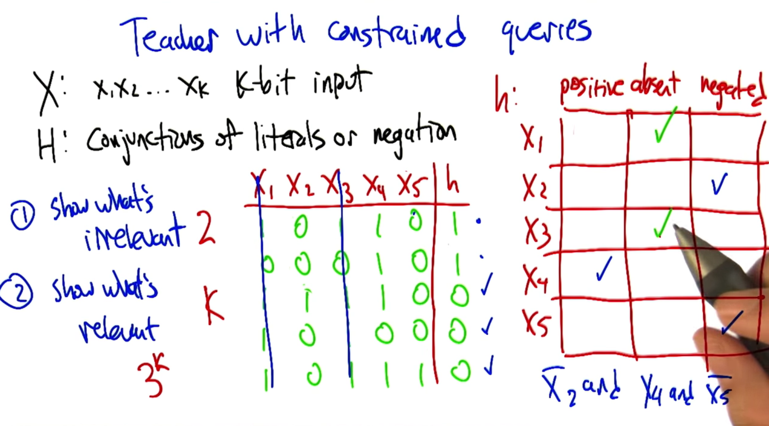
If the teacher with constrains asked questions, he can ask k+2 questions to figure out the hypothesis, which is linear

• Number of questions needs to ask: k+2
  • shows what’s irrelevant :2
  • show what’s relevant: K
• questions that could be asked = 3 ^k

• If the learner with the same constrains asked the questions, s/he will need to ask at least 2^k questions.
• most questions asked will not provide any information.

• The algorithm makes sure that the learning get a lot of information each time it makes a mistake.
• the learner will never make more than K+1 mistakes

• choose the hypothesis that are still in the version space after seeing the two training samples.

• PAC stands for probably approximately correct. 1-𝛿 confident that we will get error ε to find the true concept class h(x)=c(x).
• please note that the leaning time and samples were bounded by 1/ε,1/𝛿 and n.

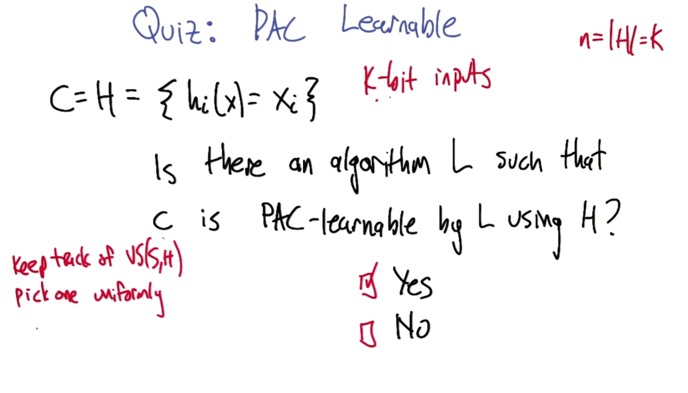
• my answer was correct but I don’t know why, keep going with the slides below.

• Epsilon Exhausted: if every hypothesis (h) in the version space have the error that’s smaller than ε, then the version space is ε exhausted.
• quiz, given the distribution of the samples data, and we only see the samples in green box, what’s the smallest ε such that VS is ε exhausted?
  • From the two instance we see, we will now only three hypothesis are possible candidates.
  • the distribution for the last instance is 0, so it doesn’t matter.
  • for the instance with 0.5 distribution, hypothesis X has error of 0.5, and OR and XOR have error of 0.
  • so ε should be 0.5 for the VS to be ε exhausted.

1. High true error: error_D is higher than ε
2. then the probability of candidate hypothesis is consistent with true hypothesis is less than or equal to 1- ε
3. then is we draw m samples, the probability of h consistent with C on all m samples is (1-ε)^m

4. then the probability of at least one h consistent with c is <= K(1-ε)m <=

   H

   (1-ε)m

5. because -ε >= ln(1-ε), so (1-ε)m <=e-εm, so that in 4, the probability of at least one h consistent with c is <=

   H

   e-εm <=𝛿 (𝛿 is failure possibility)

6. given all the above info, ln

   H

   -em<= ln𝛿, so m>=1/ε(ln

   h

   + ln(1/𝛿).

• substitute numbers in the formula above, and will get 40 as answer
• Distribution is not used

• two questions
  • what if m does not satisfy the equation? agnostic
  • what if we have infinite hypothesis? hosedness (see next lesson)

2016-01-26 完成SL6
2016-01-27 初稿完成