- Week01学习内容:
- Week 01 任务清单:
- Lesson 1: Game Playing
- Multiplayer, non-zero sum games are more complicated
- Max Number of Nodes Visited
- A problem
- Searching Complex Games
- Probabilistic games
- Further Reading
- Games
- Conclusion
Week01学习内容:
- Game Playing through Depth-limited Search;
- review/learn Python; play each other in Isolation;
- Chapter 1-2; Chapter 5.0-5.2
- R&N slides on Game Playing
Week 01 任务清单:
- Introduction on Piazza
- Start-of-Course Survey
Book used in the class Artificial Intelligence: A Modern Approach (3rd edition) by Russell and Norvig (R&N). 下载链接一,下载链接二(expired)
Lesson 1: Game Playing



- to build an AI to play the games such as “Isolation” - deterministic games
- apply minimax algorithm to play games and use alpha beta pruning to speed up the minimax algorithm
- with some modification, “expectimax” algorithm, we can also build AI’s to play games “have an element of chance.”
Challenging Quiz
The Isolation Game
- The game has two players: x and o. The players take turns, with player x moving first at the beginning of each game.
- Player x starts at position (1,1) while o starts at (8,8).
- a player can move like a queen in chess (in any of the eight directions) as long as her path does not cross a square already filled in or occupied
by the other. - After moving, the space vacated by the player is designated as filled and cannot be moved to again. Notice that only the space that was occupied is filled, not the entire path.
- The game ends when one player can no longer move, leaving the other player as the winner.
Building a Game Tree
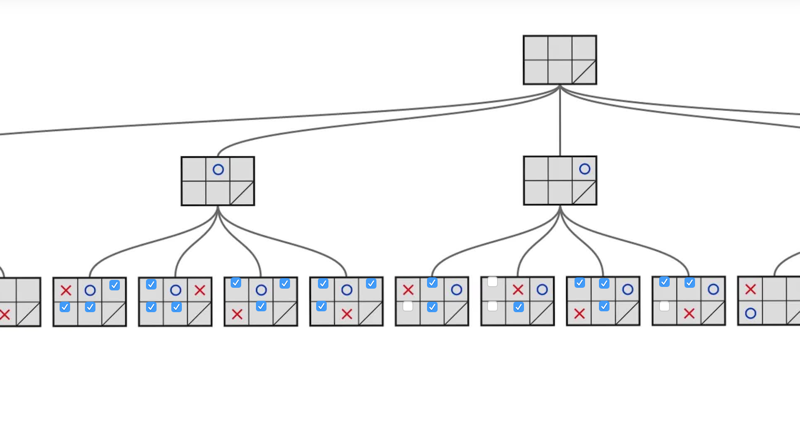
- Game tree illustrates all the possible steps of the “isolation” game.
- by examing the tree, we can identify branches that lead to a “lose” situation and warn the computer player.
- the entire tree is here: Isolation game tree with leaf values
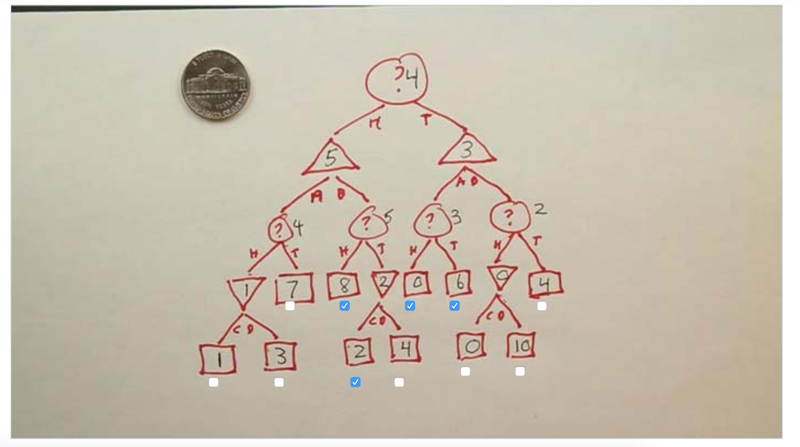
MiniMax
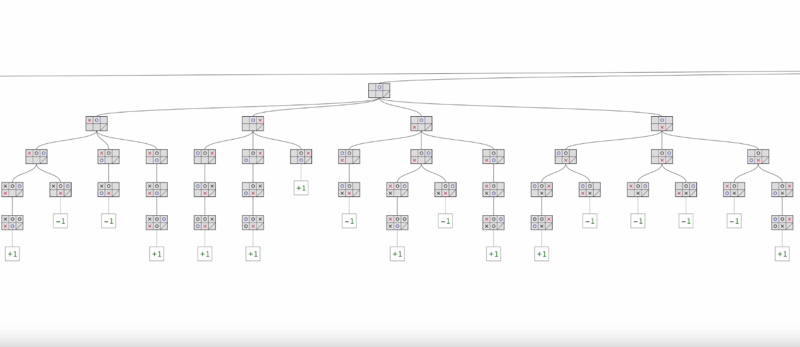
- the win (+1) and lose (-1) leaves indicated the result of each branch of the tree
- The question becomes how to figure out which first-move is the best automatically
- Minimax algorithm: computer player (AI) wanted to maximize the score to win, and opponent wanted to minimize the score to win.
- start at the maximizing level
- to determine wins or losses of a game, we need to Propagating Values Up The Tree.
- the win or lose is determined by who will make a choice at the level and how the win/loss situation is under the node.
- at the max node, choose the max value and at min level, choose the min value.
quiz
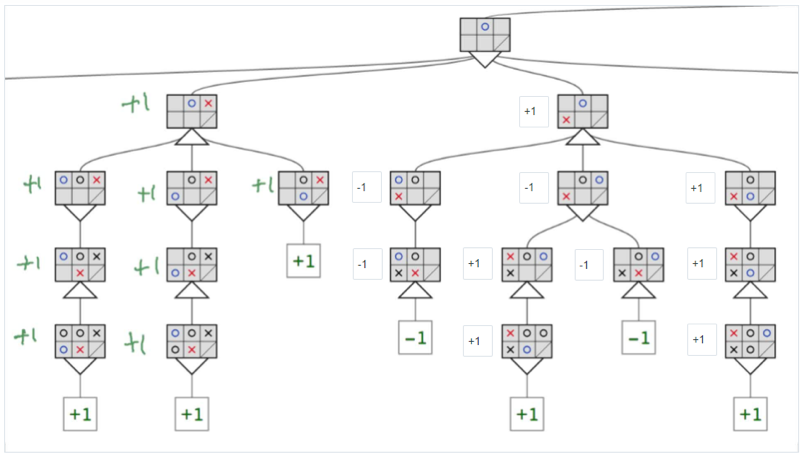
- from top-down, the second level (max level), the AI has the move so it can decide which branch to go down. Although there are two branches can lead to loss, the AI can avoid them to go to the right branch which guarantees a win.
- here is the whole tree with every node marked, download to see
Optional Reading: Artificial Intelligence - A Modern Approach (AIMA): Chapter 5.1-5.2
- s is state or note of the game tree
- the minimax value of the leaf nodes are known
- when the node is max, the minimax value of the node is the max of all the values down below
- when the node is min, the minimax value of the node is the smallest of all its subnodes.
- the decision of actions at each stage (minimax decision) depends on the minimax algorithm
The minimax algorithm performs a complete depth-first exploration of the game tree. If the maximum depth of the tree is m and there are b legal moves at each point, then the time complexity of the minimax algorithm is O(b^m). The space complexity is O(bm) for an algorithm that generates all actions at once or O(m) for an algorithm that generates actions one at a time.
Multiplayer, non-zero sum games are more complicated
for each state, its minimax value becomes a vector which contains the value for all the players there will be dynamically forming alliances, for example, A and B play against C. collaboration can also occur with just two players in a non-zero sum game.
Max Number of Nodes Visited
- on a 5x5 isolation board, the number of possible nodes is bounded to 25!, but it’s no big deal. see Quiz below: In the third move, move to which square will result in maximum options for next move?
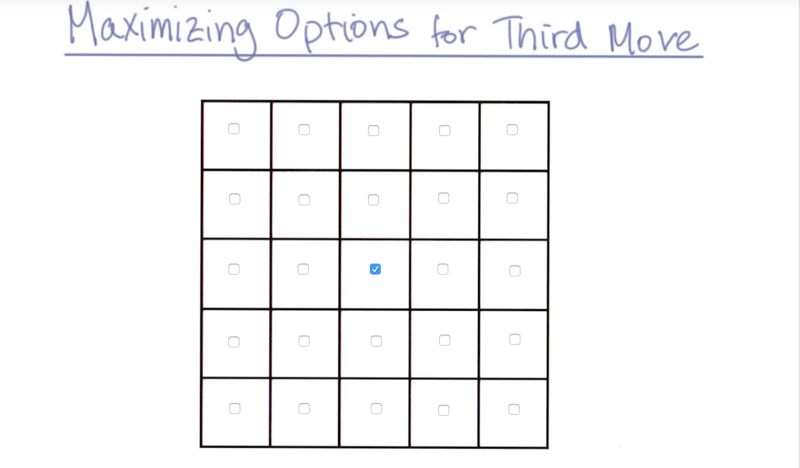
- my answer is the middle square. it has eight directions to go in the next move.
- the maximum possible number of moves from the state is 16.
the branching factor
- the branching factor indicates how many options for each move in the isolation game.
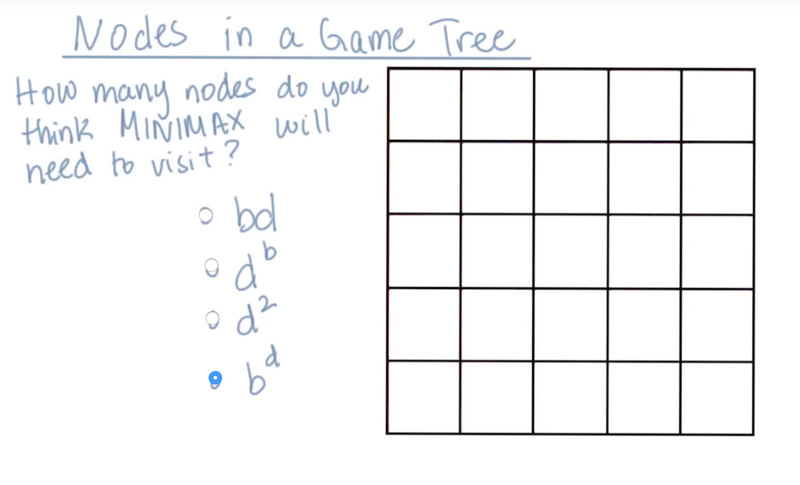
- I guessed this one and got it right. My rationale:
- branching factor (b) is roughly the number of possible move options in each level of moves. there are d levels, so the number of nodes that the minimax should visit is about b^d. b*d and d^2 are underestimated. d^b is over estimated.
an average branching factor can be calculated through game simulation.
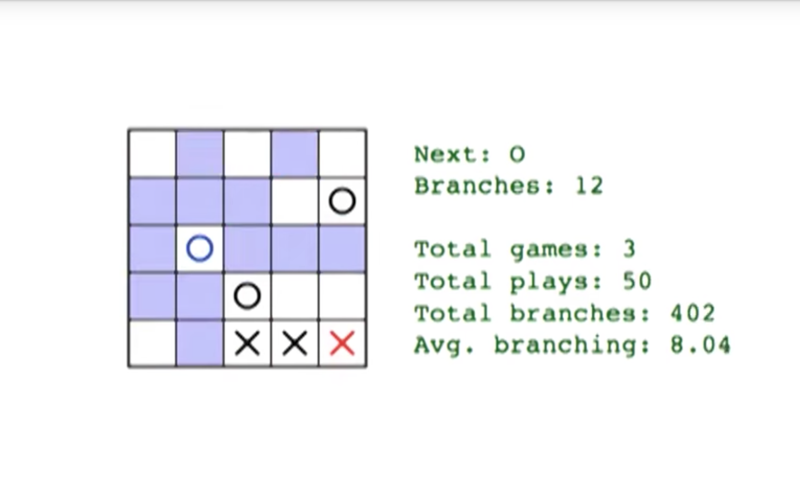
- the average b = 8. but still, there are 8^25 nodes to visit, which might take millions of year.
- The goal is, to not let the human player wait for more than 2 seconds.
- Say if the computer can visit 10^9 nodes in a second, so we need 2 seconds. based on this we can calculate the maximum depth of the game.
- 2*10^9 = 8^x; x < 10.3; here, x is the depth of the search.
- this is depth limited search: limit the depth of the search so it can finish within a deadline.
Now the question becomes “at level 9, how can we tell which node is good or bad” based on the level 10 nodes.
- an evaluation function will be needed. one way the evaluation function can be constructed to count the possible moves left for the computer player(count-my-move).
Quiz
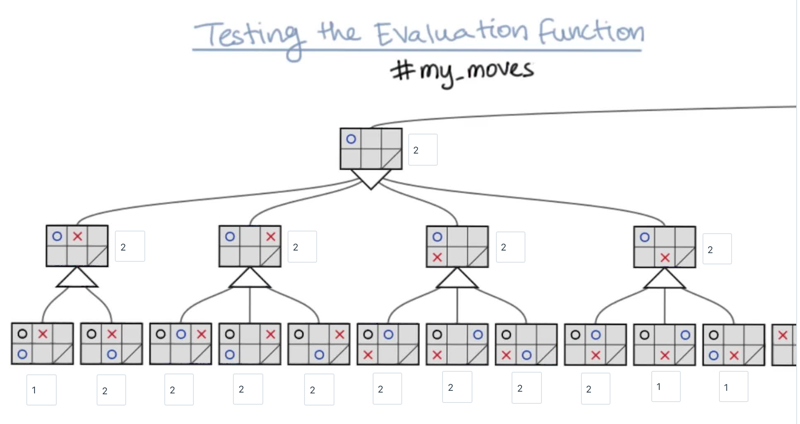
- Solution method: count the possible moves. Max level: select maximum of the lower level nodes; Min level: select the minimum of the lower level nodes
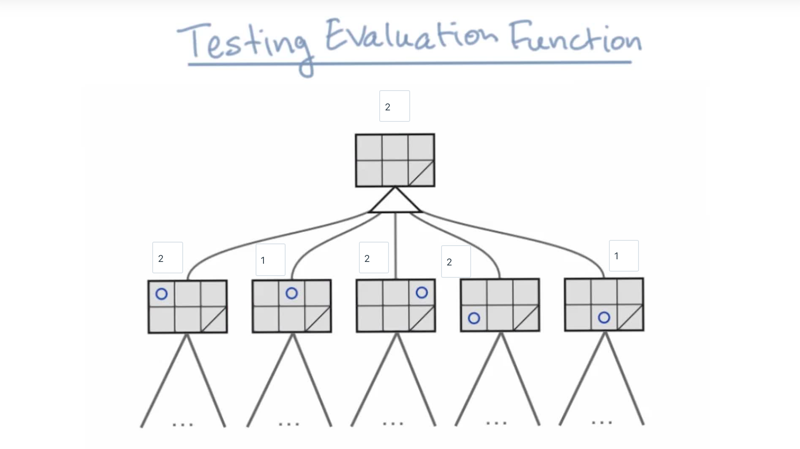
- Click to open: Isolation Game Tree - Level 3
- do the calculation for the whole tree.
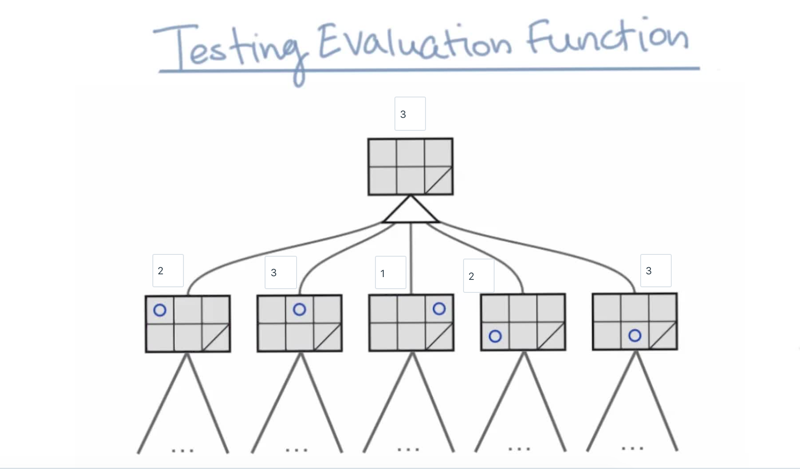
The results do not agree with the results of level 3 tree. Which means when to search for level 2 and level 3, the evaluation function will give a different answer.
- It does not mean the evaluation function does not work
- it might mean the search is not deep enough.
- we can go deep to reach the point that when deeper in levels did not change the result.
A problem
- we try to avoid going deeper because the number of nodes increases exponentially as we go deep.
- Quiescence search is an algorithm typically used to evaluate minimax game trees in game-playing computer programs. It is a remedy for the horizon problem faced by AI engines for various games like chess and Go.
- Trick: interactive deepening.
interactive deepening.
- the problem: return the best answer before time run out (2 seconds).
- Steps:
- search level 1, record the best answer, answer 1.
- if time is up, return answer 1, if not, search level 2 and get the best answer.
- check time, if time is up, return level 2 answer, if not, deepen the search to next level …
As we deepen the search, the number of nodes on the tree and the interactive deepening nodes increase
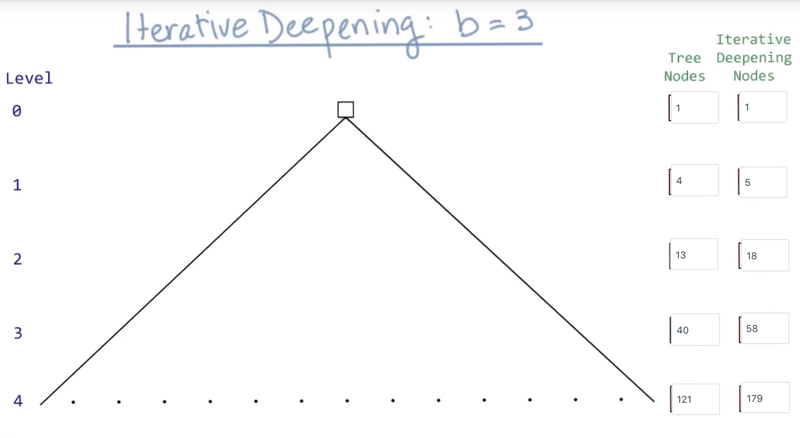
- when b = 2, n = 2 (d+1) - 1
- when b = 3, n = (3 (d+1) - 1)/ 2
- when b = k, n = (k (d+1) - 1)/ (k -1)
interactive deepening on Isolation game
- branching factor of the Isolation game varies
- at the beginning of the game, branching factor (B) is large, and searching needs more time.
- at the end of the game B is smaller, and searching is shallow. So, we might need to develop strategies to allow the player to take more time at the beginning or the middle of the game, but less time in the end game.
Horizon Effect
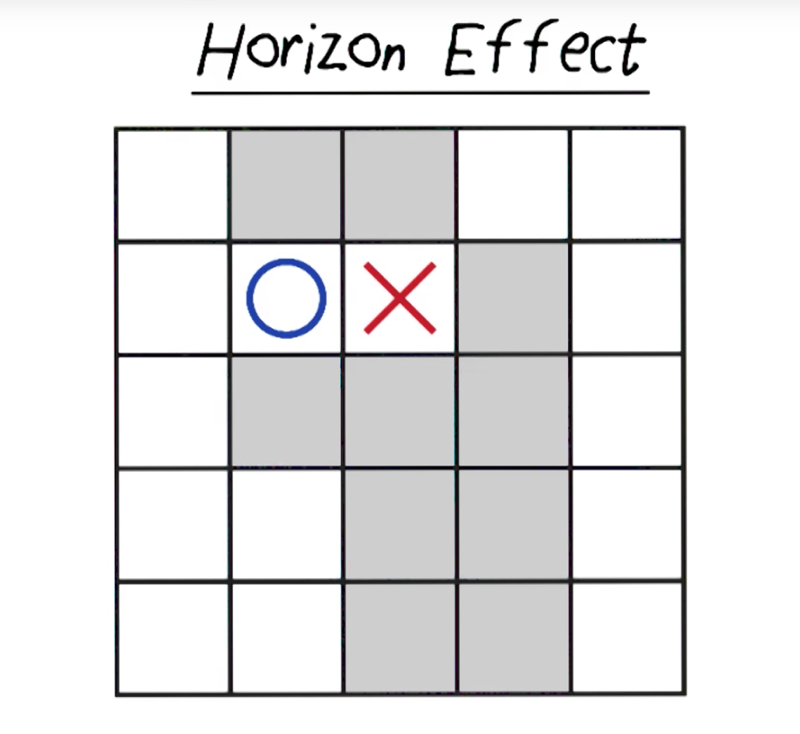
In the above situation, it is very easy for a human player to observe that O takes the move next to X will when because it will allow X to have 6 moves but O has seven (because a partition is created).
But it will take the computer to search 13 levels to figure this out (which we don’t have enough time to do).
This is the horizon effect.
So we need evaluation functions. to check partition. but it might increase the search time. So good evaluation function need to balance between dealing with horizon effect and simplicity or effectiveness.
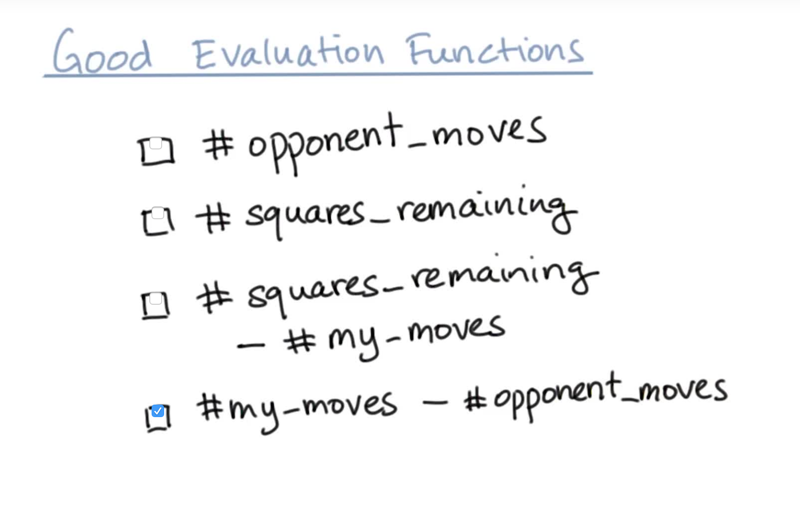
- the answer was chosen based on that it is more likely to be positively correlated with the chance of winning
-
the new evaluation question can lead to the correct move for this board. Evaluation function should represent a good winning strategy (but it is not always guaranteed).
- my-moves - #opponent_moves might be an even better evaluation question.
Alpha-Beta Pruning
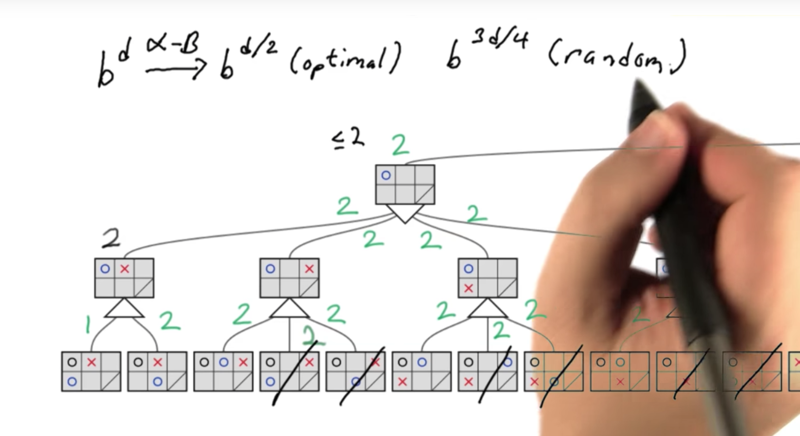
Alpha-Beta Pruning allows the AI to skip a section of the game tree but still get the same answer of the minimax algorithm. [More efficient than minimax]
It can reduce the search time to bd/2 ~ b3d/4

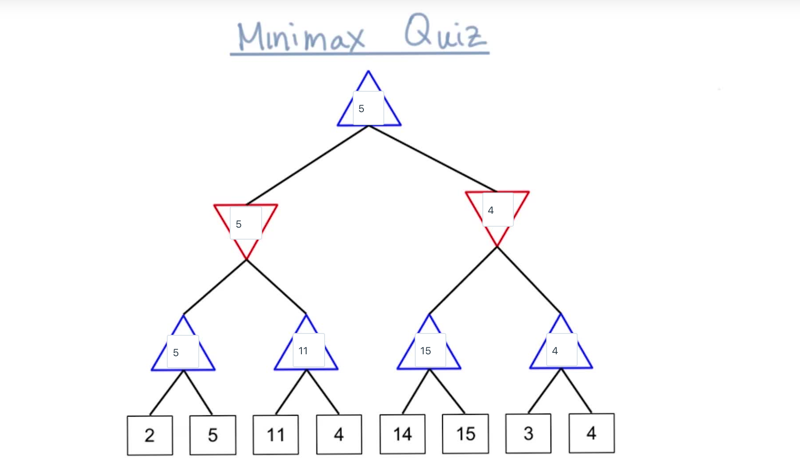
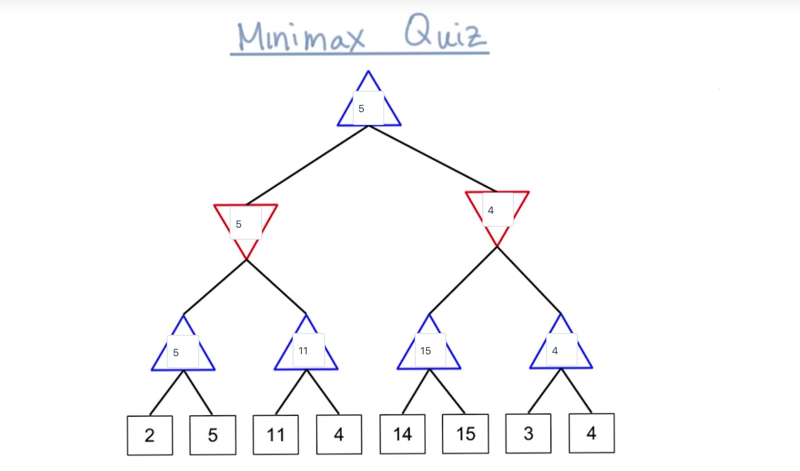
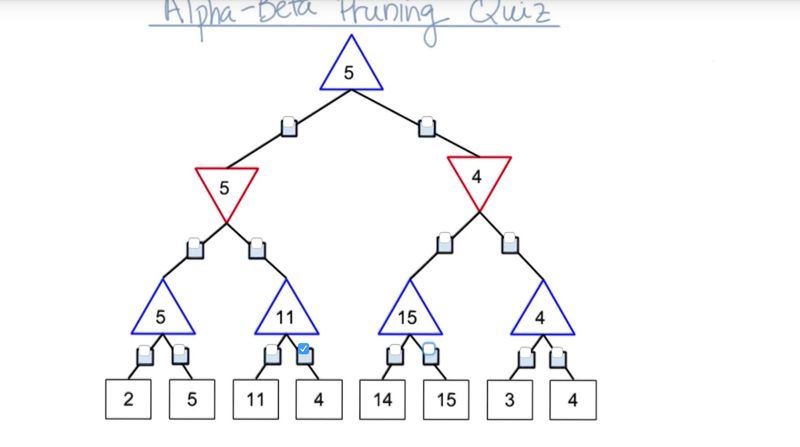
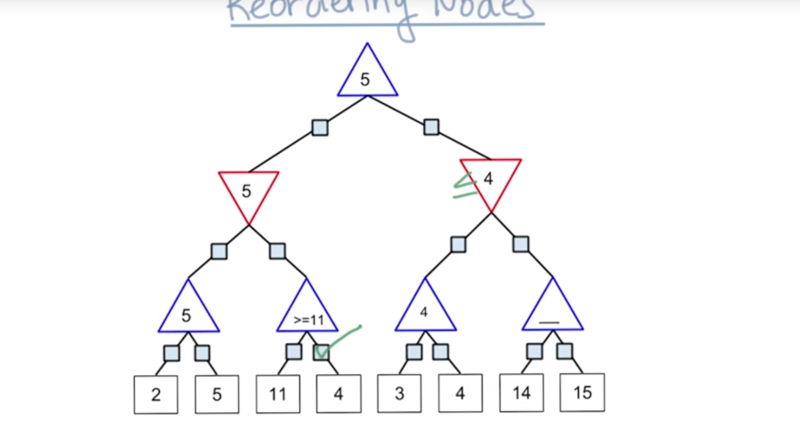
Searching Complex Games
Reading AIMA: Chapter 5.3-5.4 [Done, did not track time]
Solving 5x5 Isolation
Some strategies for the 5x5 game: open game search table; check for reflections to minimize the open game; occupy center; reflex move; minimax and alpha-beta pruning.
3-Player Games
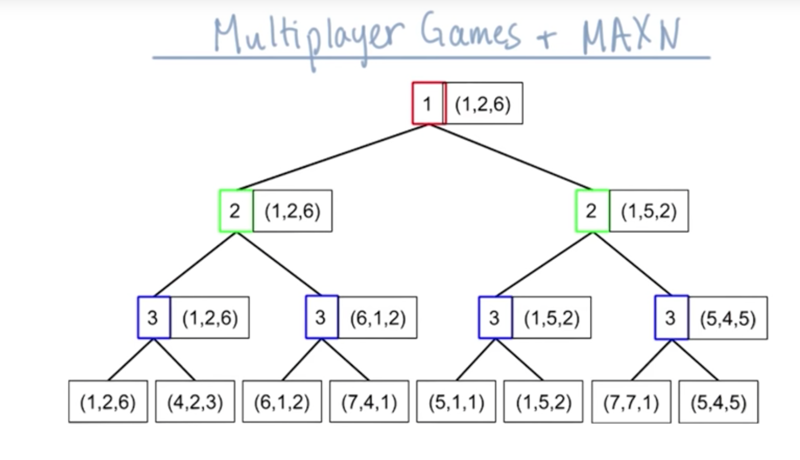
- minimax doesn’t apply for a 3-player game, instead, we evaluate each node based on which players move at each move.
- the end node will be a vector of utility for each player.
- max-N algorithm
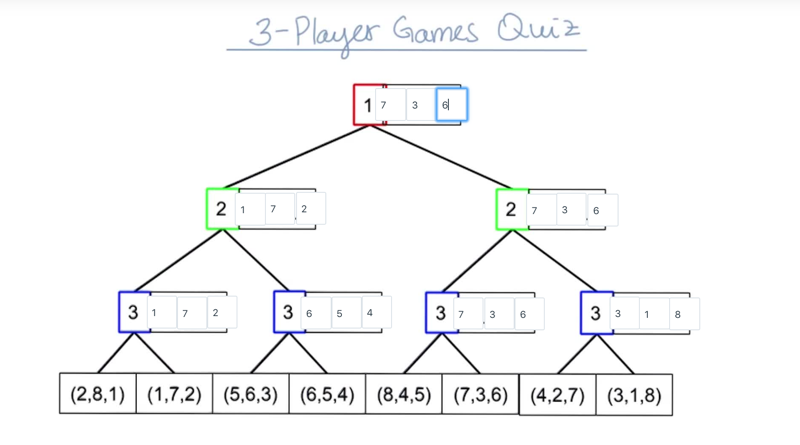
3-Player Alpha-Beta Pruning
- Question: can alpha-beta pruning work for 3-player games?
- Answer: as long as the game utility has a lower-bound and individual utility has an upper-bound, then yes.
E.g., shallow pruning and Immediate pruning are possible, but not deep pruning (why?)
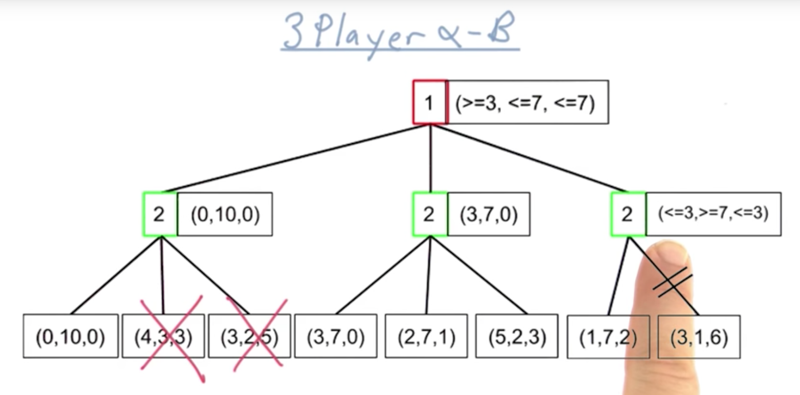
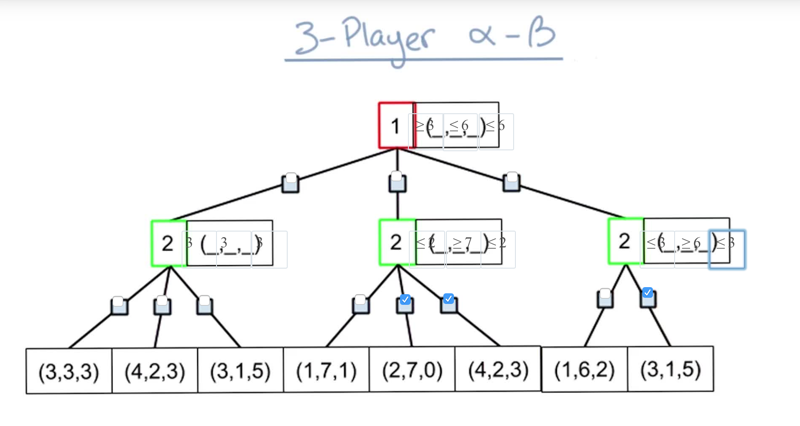
- from the most left nodes, we get (3,3,3) for move 2 based on player 2’s preference
- Thus, player one should have a value which is >= 3.
- in the middle branch, after evaluating the most left node, player 2 will update its value when the value is >=7, and make value for player 1 to be <= 2, but player 1 already had a better solution, then there is no need to look for the other 2 nodes in the middle branch.
- same logic will determine the last node can be pruned.
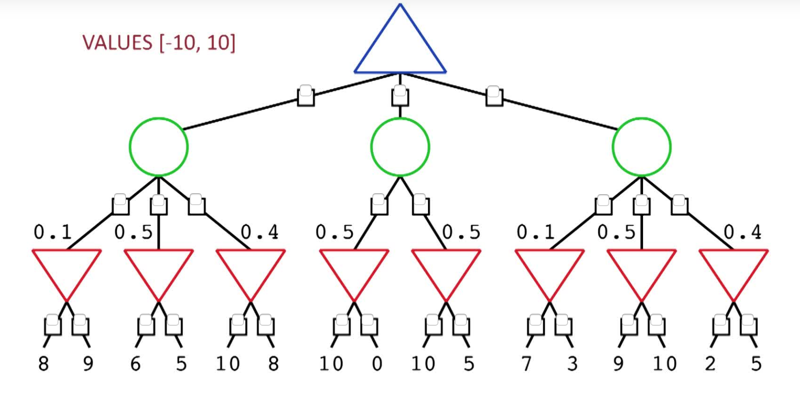
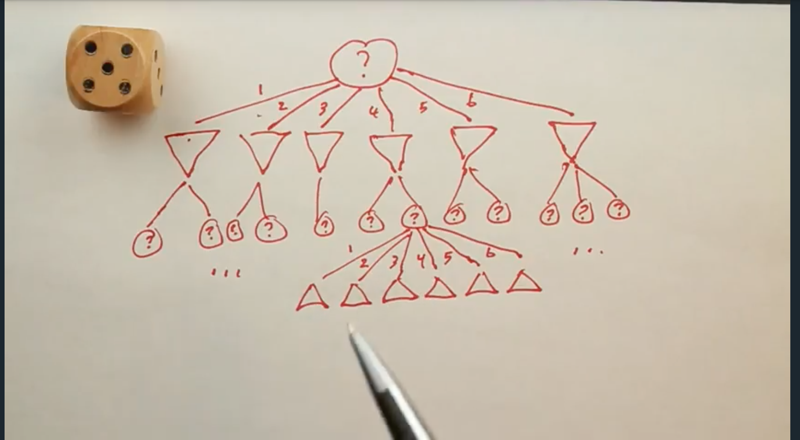
Probabilistic games
One type of probabilistic games is that each action might lead to two or more states with a certain probability. Sloppy isolation is an example:
Sloppy Isolation
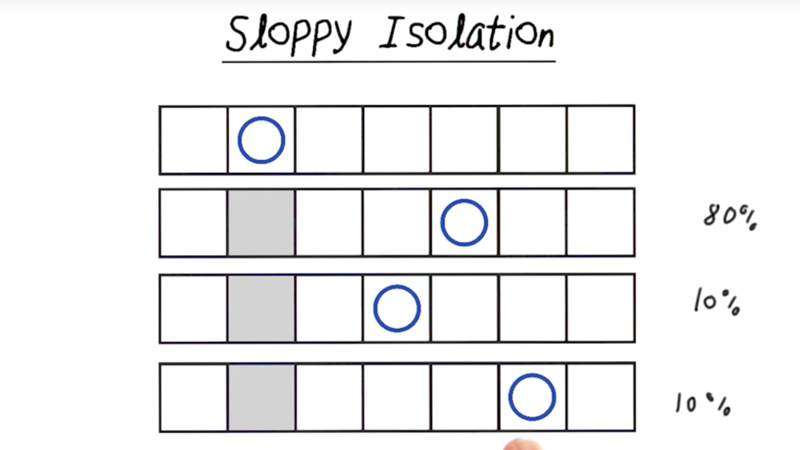
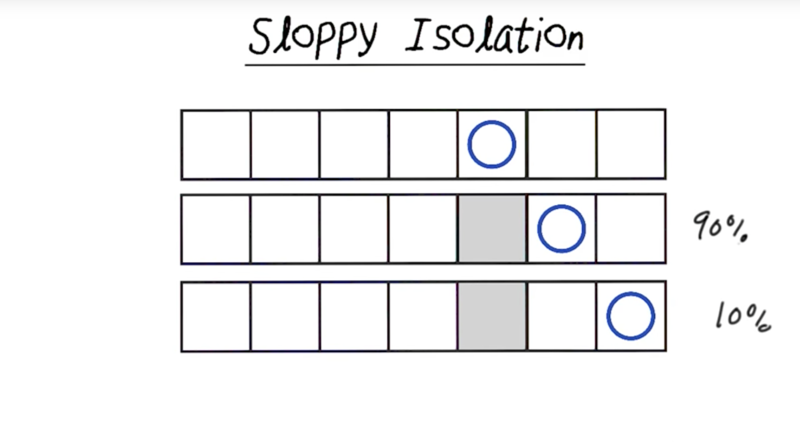
In this version of isolation, the player might overshoot or undershoot with a 10% chance for each error, and the player will have 80% chance meet the goal.
This can be complicated as the player’s moves were limited by available of squares. E.g., sometimes there will be no chance of undershoot or overshoot (see pic above). In this case, the change of hitting the target will be 90%, and the chance of overshoot/undershoot will still be 10%.
expectedMax
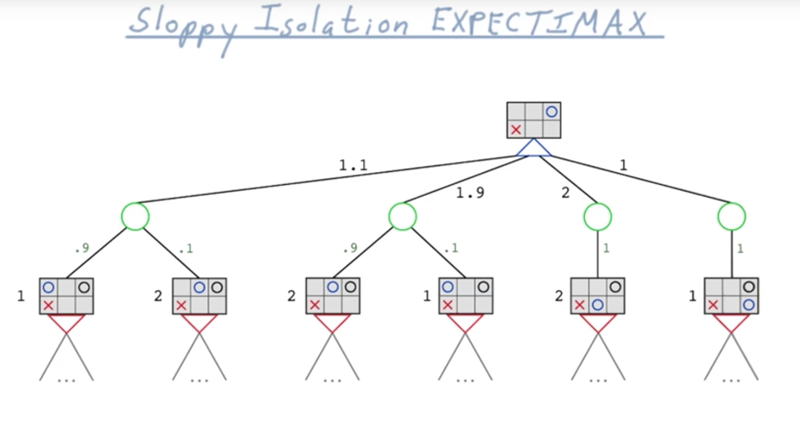
When populating the game tree, we need to generate branch and leaves based on a probability of hit or miss the target.
Pruning might still work.
##
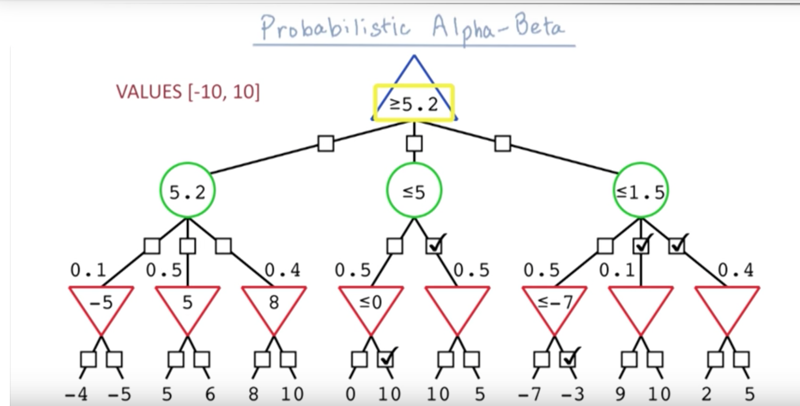
Further Reading
Peter Norvig and Sebastian Thrun’s lectures on Game Playing and Game Theory.
Games

- St: stochastic games: MDP is for ST
- PO: partially observable games: POMDP is for partially observable environment
- U: Unknown games: RL deals with Unknown environment
- CL: Computational limitations: A* search, h functions, and Monte Carlo focus on computational limitations.
- A: Adversaries: there are more than one players play against each other.

Single Player Game
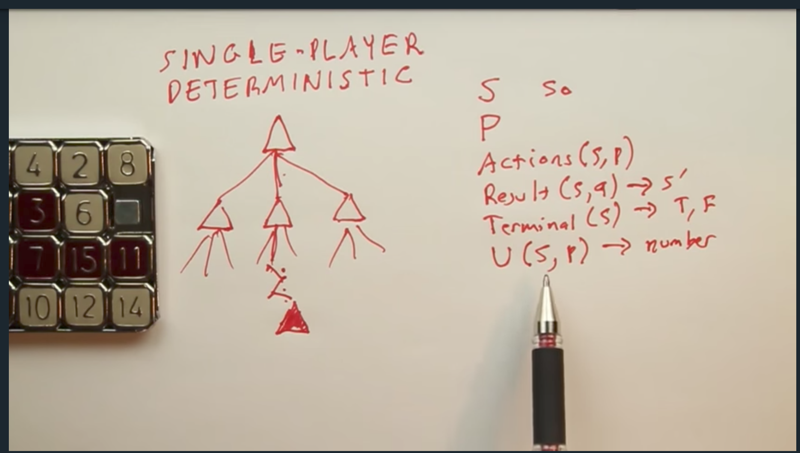
- to solve a single player game, the player needs to explore the game tree until finding the goal state, and then backup to find the path to the goal state.
- On the left of the screen, parameters to describe a game are listed. state, player, action, transition function, utility function, terminal state checker, etc.
Two Player Game
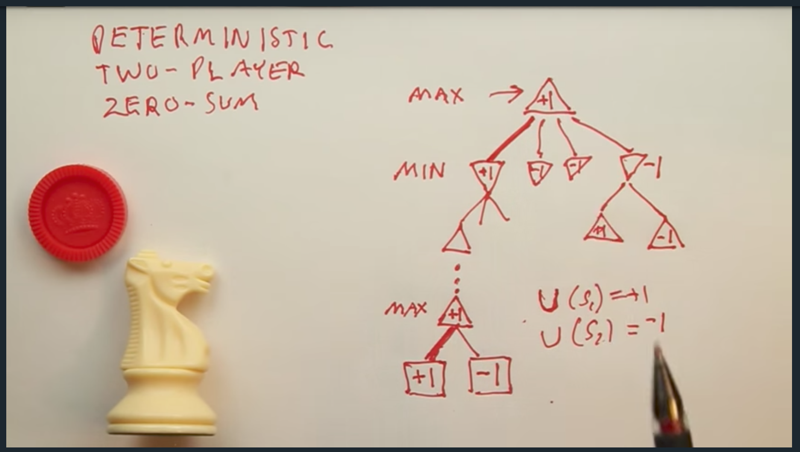
- Two player adversary games can be solved by MiniMax algorithm while player Max will maximize its utility, and player Min will minimize Max’s utility.
- The tree search will go all the way down to the terminal state. Utility function will define the utilities of terminal states. When the search reaches the terminal, the value of the path will back-up to the start state. the player will choose the path based on its utility in each state.

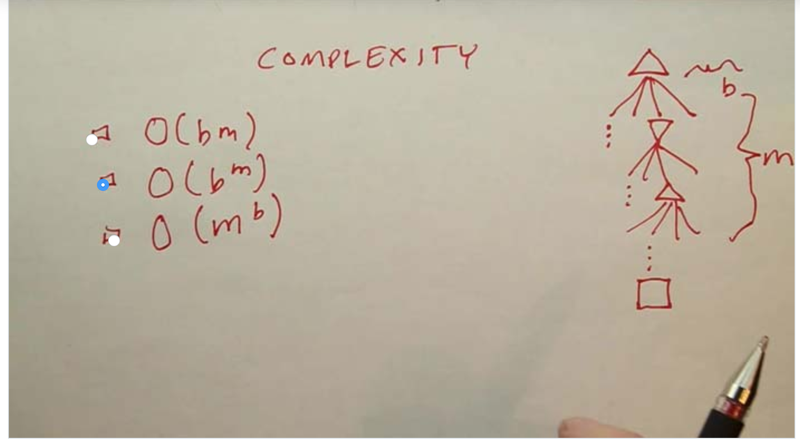
- b is branching factor, m is the depth of the game tree.
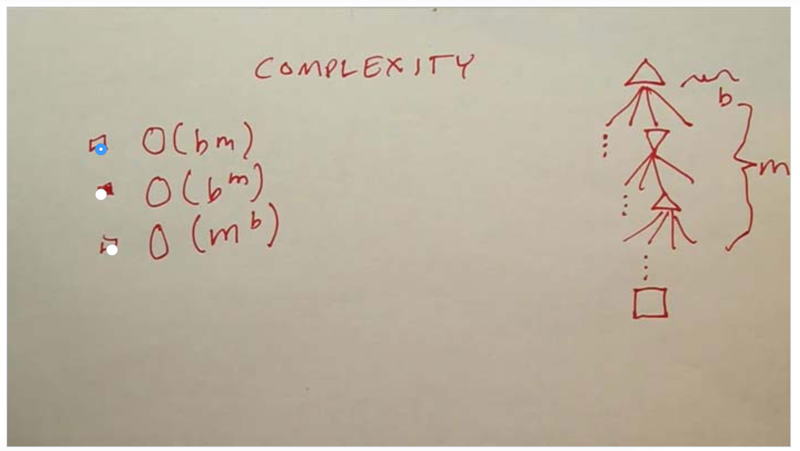
- the space complexity is better than the time complexity.

- given b=30, m= 40, and we can use all the computers in the world, search through the tree of a chess game will take forever.

- to deal with complexity problem, we need to try to reduce b, m and the structure of the game representation.
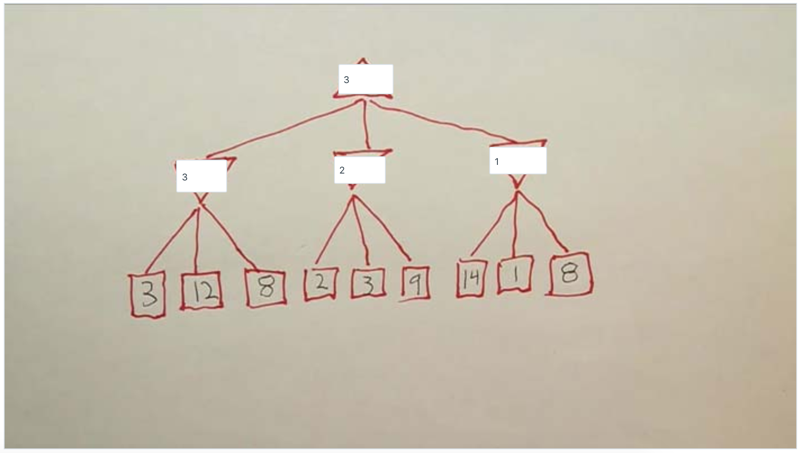
- fill in the utility for each node.
reduce B
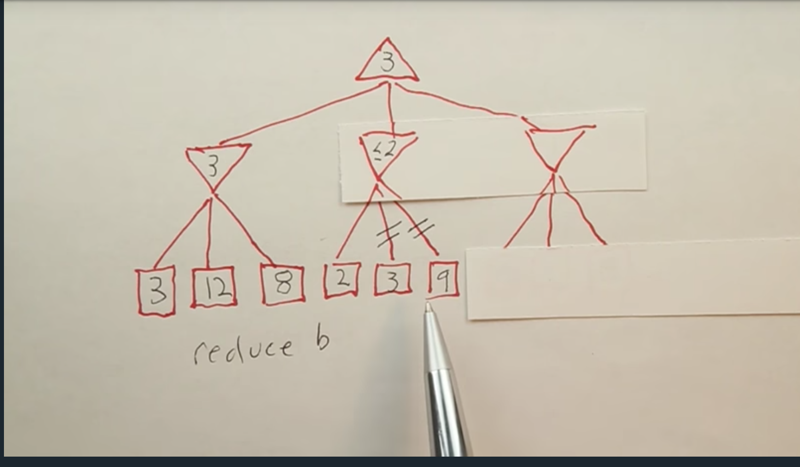
- the first path in the middle node can define the value of the second node in the min level will be less than 2, which can never be large than 3, so no matter that value of the two terminal nodes will be, the results of the top node will not change. Thus, the player doesn’t need to visit the two nodes. Pruning means to ignore some nodes to reduce the branching factor b.
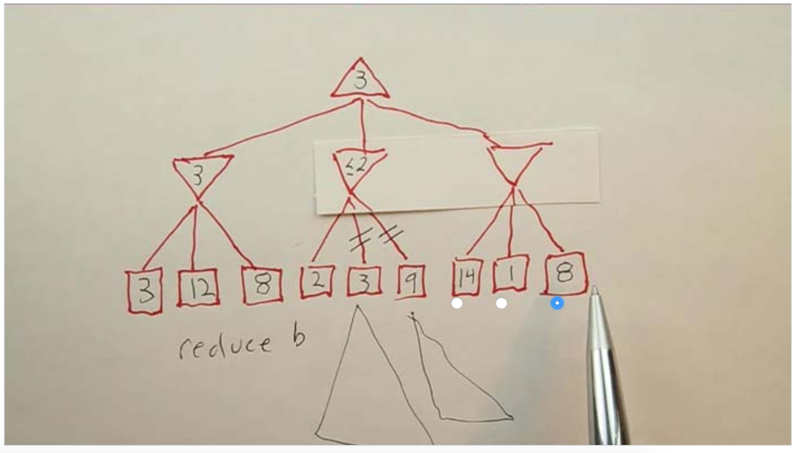
- the 8 does not need to be visited since the upper node needs to be less than 1 to be updated, which is smaller than the current best answer for the top node.
Reduce M

- Cut off the search at a certain depth. Since we did not reach terminal yet, we can not use utility function. Instead, we can use evaluation function.
- Here, the evaluation function will be the keep to win the game. and this method is the Alpha-Beta pruning.
- Alpha-Beta pruning can reduce the game from a O(bm) problem to a O(bm/2) problem if the tree nodes are ordered perfectly.


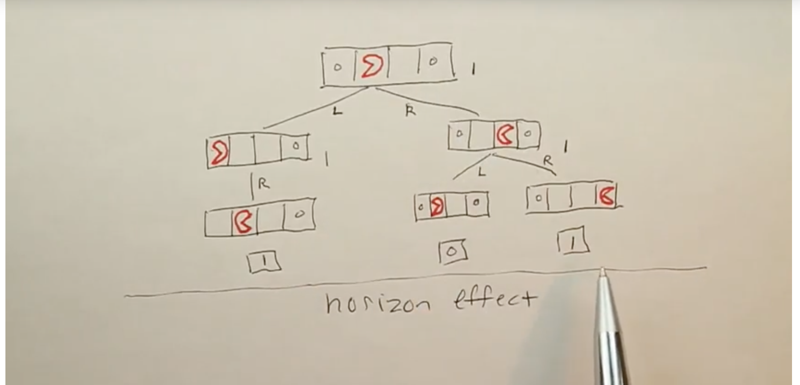
- Cutting off depth of search can suffer from Horizon Effect
- When in the certain cutting off the depth of search preventing the player to see the real winning path, it can give the wrong answer. Unless the searching depth gets deeper, the player will never reach the node which can decide the winning path.
Dealing with stochastics

- using the expected-value function for the chance node.
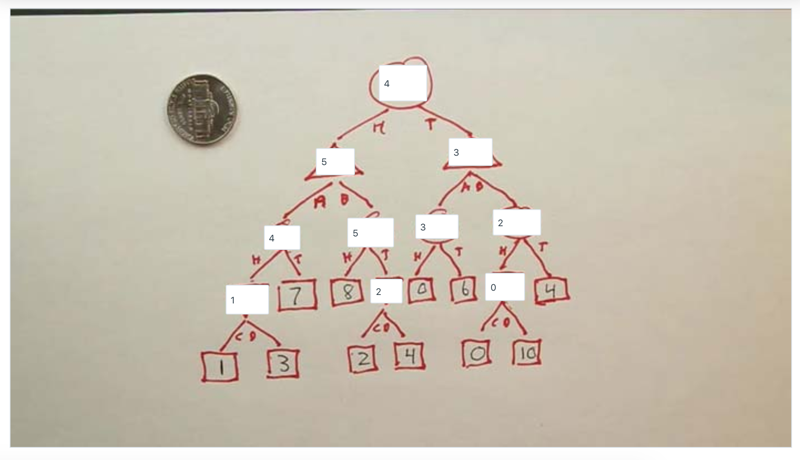
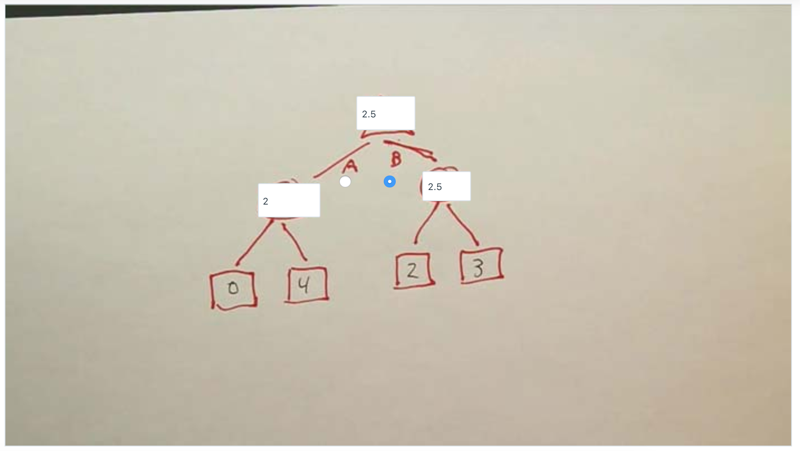
- The game could start at the left or the right branch. if starting at 5, player max will choose b, if start at 3, it will choose A…
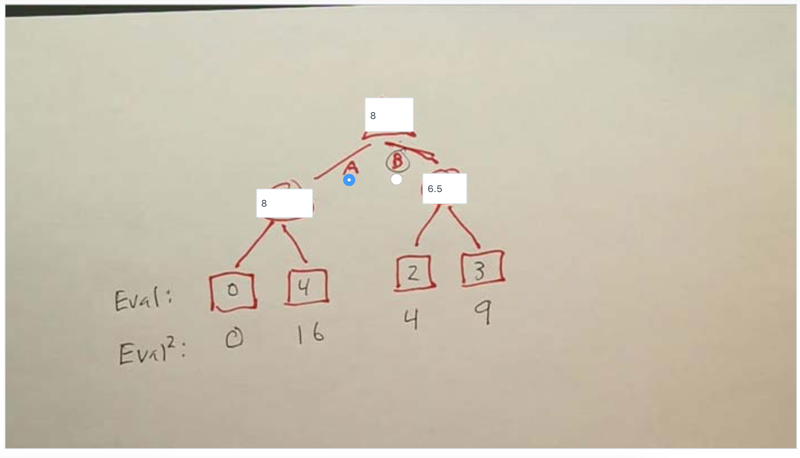
- The above two quiz showed how evaluation question can affect the player’s choice.
Conclusion

- Minimax algorithm uses maxValue() and minValue() to find out the value of a state.
- if the state is the terminal state, then its value is defined by the utility function.
- to reduce the complexity of the problem, we can cut-off the search at a depth level and use Evaluation function to determine the value of the states.
- When a state is stochastic, it’s value is determined by a expValue() function.
- alpha and beta will be used for pruning the tree.
Example codes for Games, or Adversarial Search. (Chapters 6)
``` 2017-09-10 First draft, took 6 hours To do: all the readings in the section. Notes of the reading should be done.
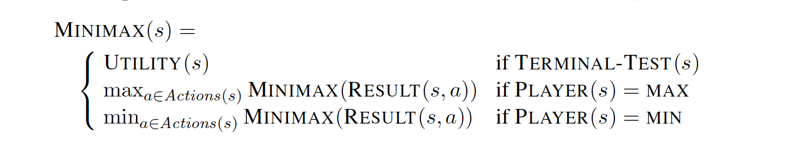
Preview: