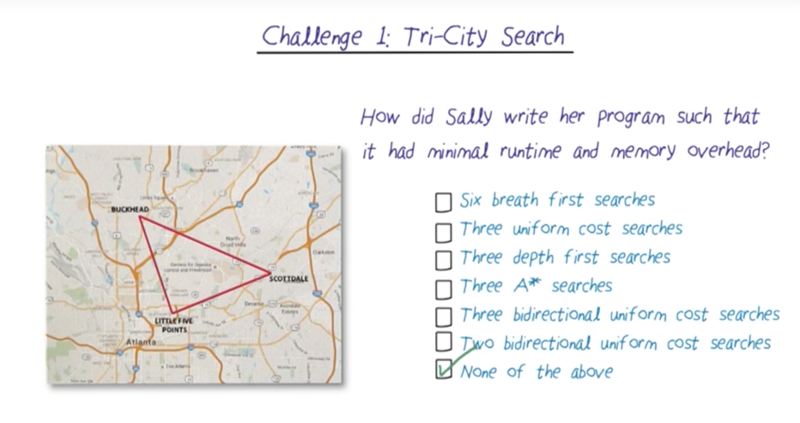
• challenge question
• Introduction
  • Example Route Finding
• Tree Search
  • Breadth-First Search
• Graph Search
• Uniform Cost Search (AKA cheapest-first search)
• Search Comparison
• Complete means if the search tree or graph is infinite, the search algorithm can still manage to find the end goal.
• More On Uniform Cost
  • Greedy best-first search
• A^* Search
  • Optimistic Heuristic
• Vacuum world
  • Sliding Blocks Puzzle
• Readings
• Challenge Question Revisited
• Peter’s Take On AI

This week you should watch Lecture 2, Search, and read Chapter 3 in AIMA (Russell & Norvig).

challenge question

Readings Korf, 1997. Finding Optimal Solutions to Rubik’s Cube Using Pattern Databases. God’s Number is 26 in the Quarter-Turn Metric.

Introduction

• Problem-solving: the theory, and technology of building agents to plan ahead to solve problems
• A problem is unsolvable if there is no goal state.

Elements of a problem

• initial state
• given a state, give a list of possible actions in the current state.
• result function: given the state and a selected action, then reach a result (not always new) state.
• goal test function tells the agent if the current state is the goal
• path cost is the cost if an agent taking the given path
• the step cost is the cost of taking an action from on state to reach a new state.

Example Route Finding

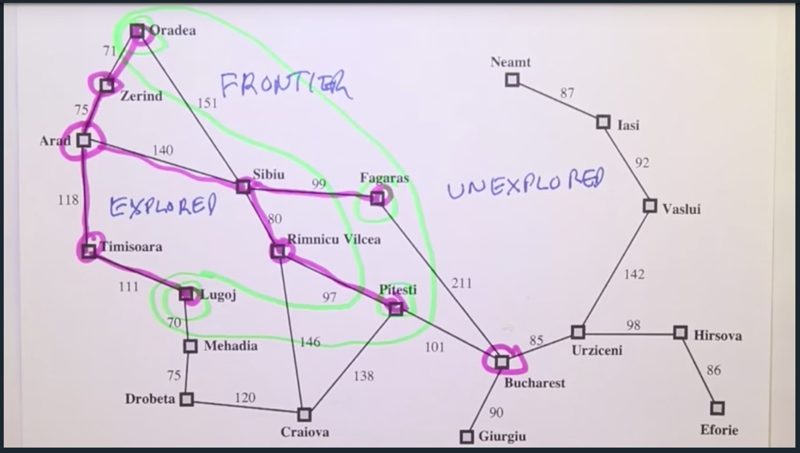
• Here we have 3 regions in the problem world: Frontier, explored and unexplored. the frontier is the states in the green region, they are the end state of the current path. Explored states are the states on the search path explored. The unexplored states are all the states in the search space which are not part of the searched pages yet.
• Step costs are distances between cities and path cost is the sum of the step costs of all the steps on the path

Tree Search

• Tree search is a set of algorithms: There are multiple ways to choose the frontier

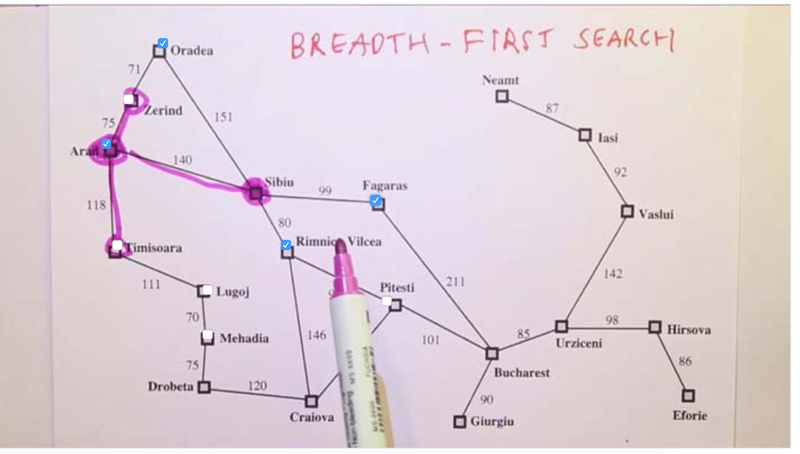
Breadth-First Search

• with the Breadth-First search, the algorithm always choose to explore the shortest path. In the example above, Arad goes to Zerind, Sibiu and Timisoara are the three shortest paths ( short in terms of depth, not distance or cost).
• Quiz: Given Tree search, we are going to explore sibiu’s next step, which city will be explored?

• Answer: Rimic Vilcea, Fagaras, Oradea and Arad
• Note: tree search will not know if the search resulted in a back-track path. (Thus Arad was explored again).

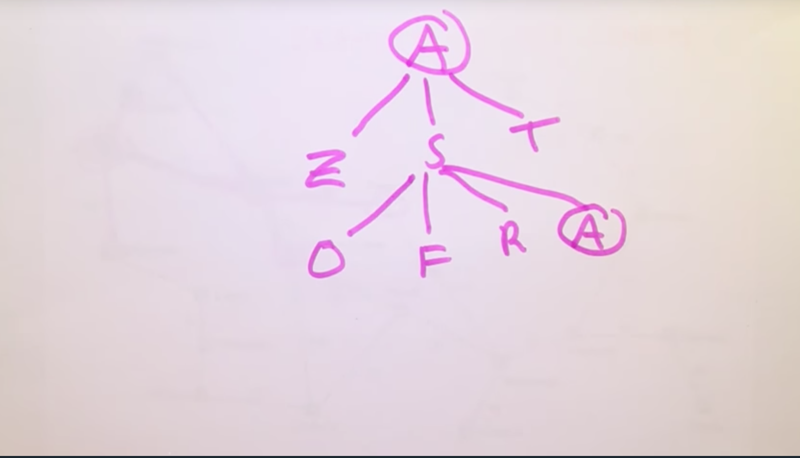
• So we need to track the “explored region” and the frontier region of the tree. By comparing the states in the frontier and the explored region and removing the states that are in both the region so that they won’t be visited again to avoid repeated search, that’s what Graph Search will be doing.

Graph Search

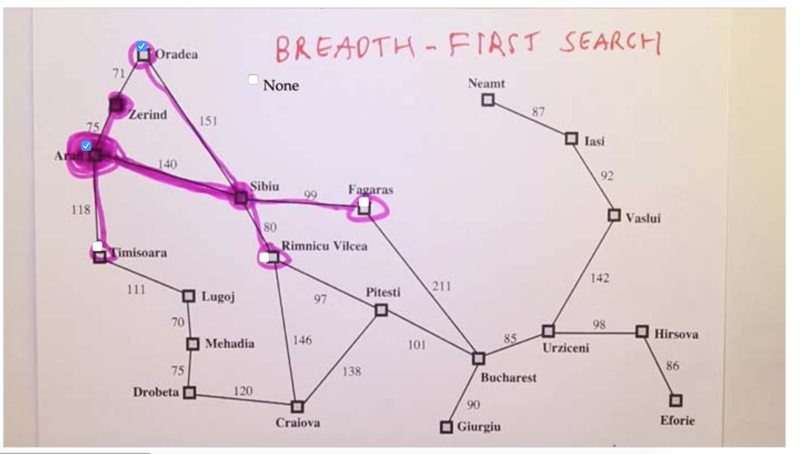
• Question, given the current state (Zerind) and paths in the frontier, which states should be explored next?
• answer: nothing to add since Orada is already in the frontier and the path won’t go back in a graph search algorithm because of the bread-first search

• the next state is the target city Bucharest
• No, the problem is not solved, even the agent reached the target state.
• the search won’t stop when we add the goal state to the frontier
• because the problem is not just to reach the target goal, but to meet the goal with the shortest path.
• in this case, the upper path has shortest steps, but the cost might not the smallest. To determine it, we have to keep expending the frontier. Only when a path expending out the goal state first, we can say the path it is under is the shortest in terms of the total cost.

Uniform Cost Search (AKA cheapest-first search)

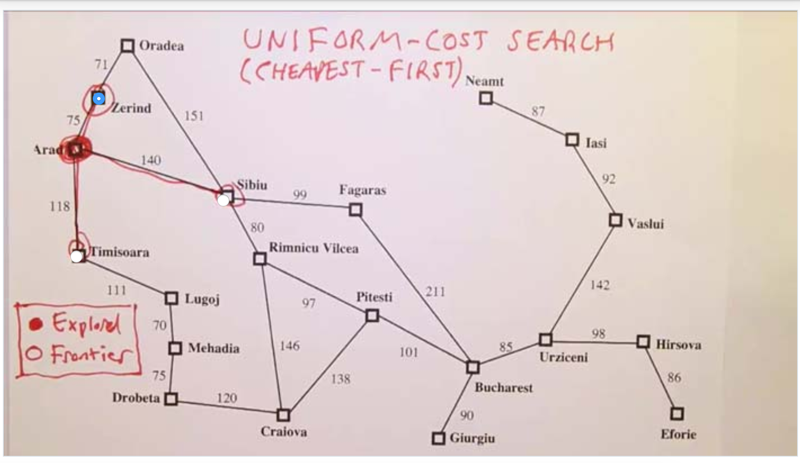
• given Uniform Cost Search, the agent chooses the path with the cheapest cost first, thus, the Zerind path is chosen first.
• after this, the cheapest path becomes Arad->Timisoara

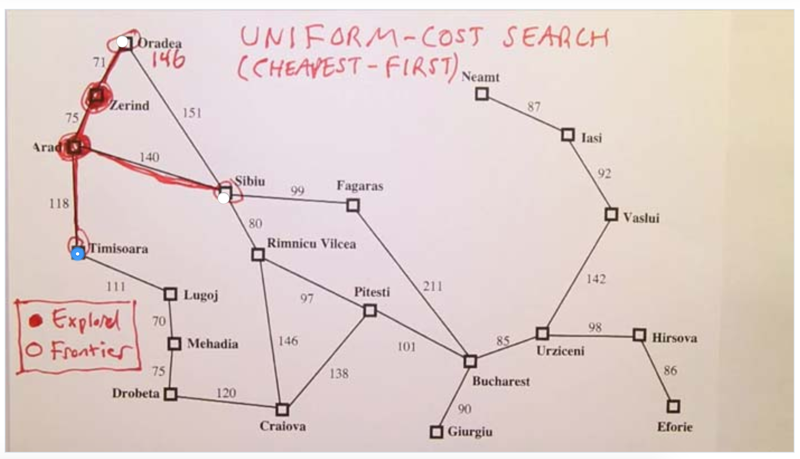
• after each expansion of the frontier, the length of each available path will be evaluated and the cheapest path will be chosen to expand, until the goal state is reached.

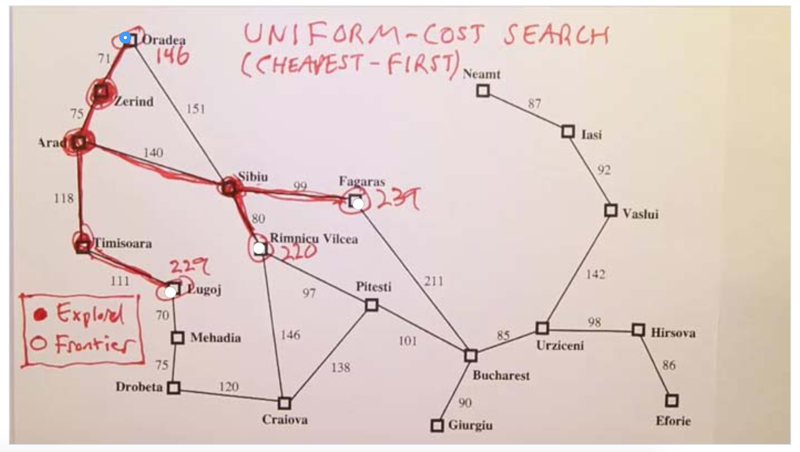
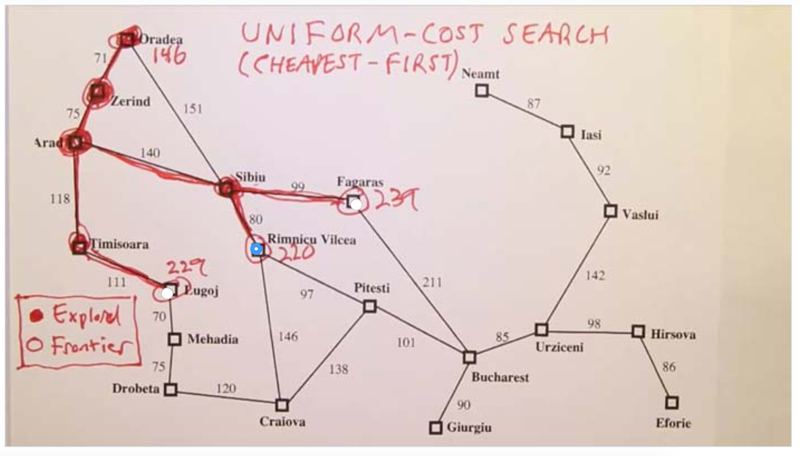
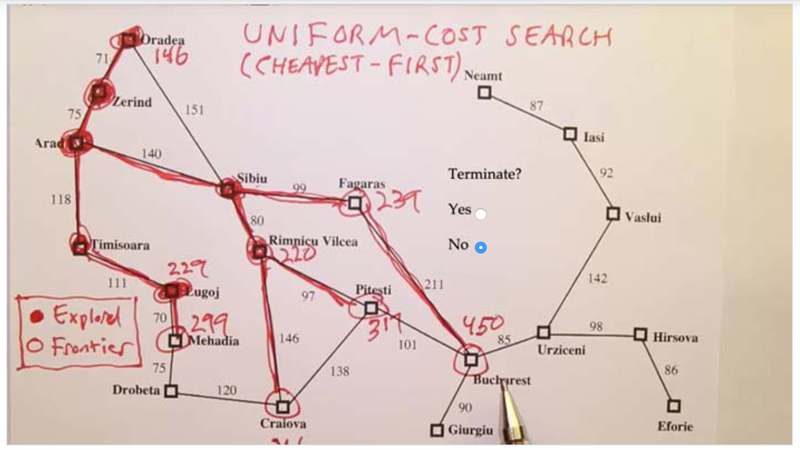
• The search won’t stop when it reaches the goal state. why? because the path reaches the goal the first because the path before it reaches the node before goal was the shortest, but it could travel very long to get to the end.
• The search will stop when it is moved out of the frontier not when it is added to the frontier

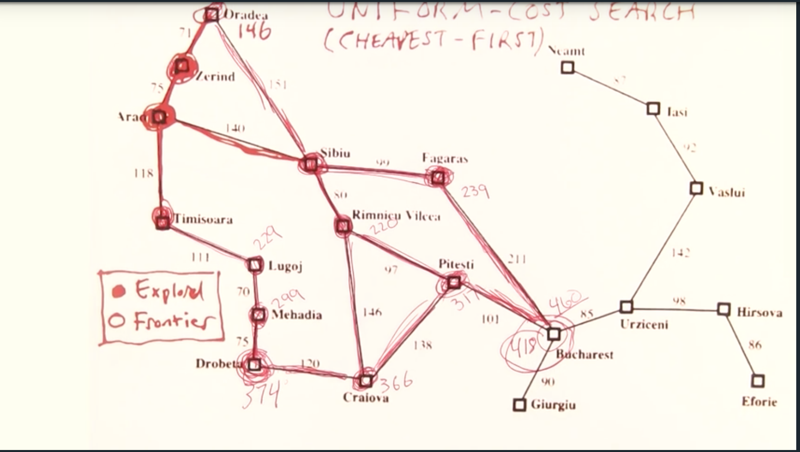
• the search going and we will find the path with a cost of 418 is the one pop out the goal state from frontier first.
• and this is how the uniform cost search guaranteed the search of the cheapest path

Search Comparison

Breadth-first V.S. Cheapest-first V.S. Depth-first

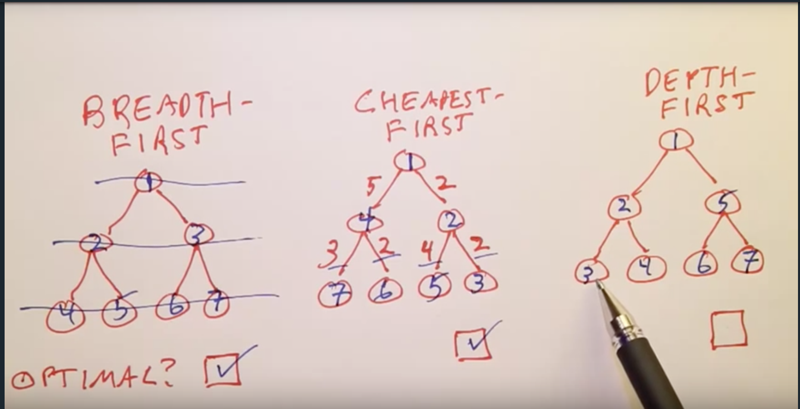
• Optimal means the algorithm is guaranteed to find the results
• for BFS, it is the path to the goal with shortest steps, for CFS, it is the path to go with the smallest cost
• for depth-first search, it is not guaranteed to find goal because the goal might not even be selected if it is not on the path of the longest depth.

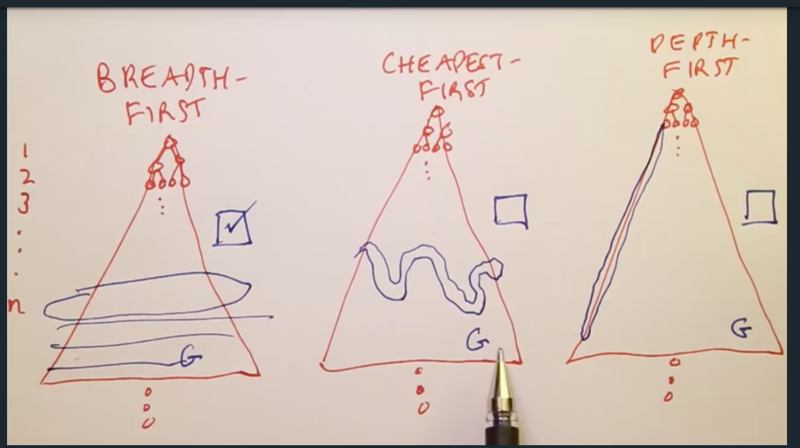
Complete means if the search tree or graph is infinite, the search algorithm can still manage to find the end goal.

• Breadth-first and cheapest-first are complete
• Depth-first is not complete given infinite steps of the tree if the goal is not on its search path.
• But the depth-first tree saves search space ( uses less memory).

Clarification on cheapest first search:

Consider an infinite path whose costs are as follows: 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + … The infinite sum of this series in the limit is 2. If the shortest path to the goal node has a cost greater than 2, the cheapest first search will be incomplete.

More On Uniform Cost

Uniform Cost will cost a lot of time when the search space is large.

• Greedy best-first search can use smaller steps to reach the goal
• but when there are obstacles on the way, the greedy best-first search will spend more time to find the goal
• solution: combine Uniform Cost with Greedy Best-First search, that is A^* search

Greedy best-first search

• It needs some new knowledge, e.g. use the straight-line distance between the current state to the goal to guide the search direction. it means to expand the node with the shortest distance to the goal first. but it will not be guaranteed to find the shortest path when there are obstacles ( see the graph below).
• But there is a solution the combine the best of Uniform cost search and greedy best-first search. It is the A^* ( A-star) search.

A^* Search

• In A^* Search, we need to minimize g and h functions at the same time so that we will have the cheapest the path and also focus on reaching the goal.

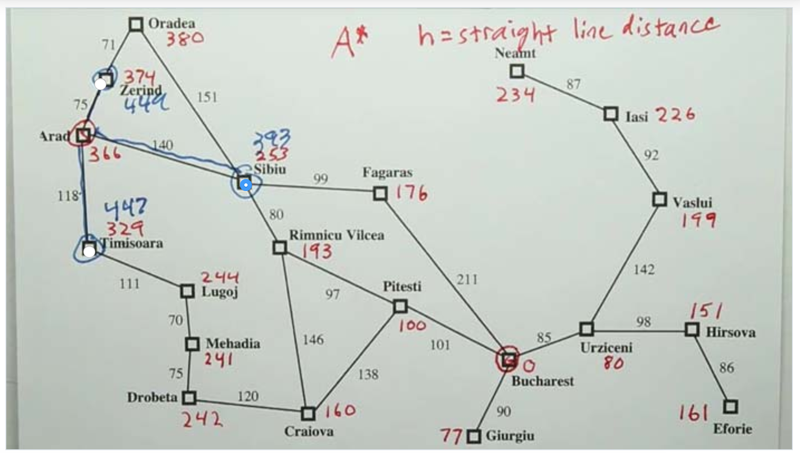
• here, g is the cost, h is the estimated the strait-line distance between each city to the goal.
• A* chooses the smallest g + h as the path to explore
• for the paths, see figures below

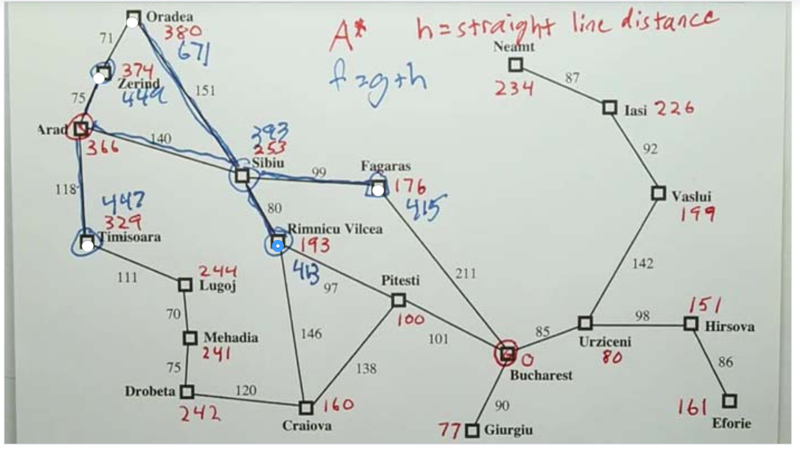
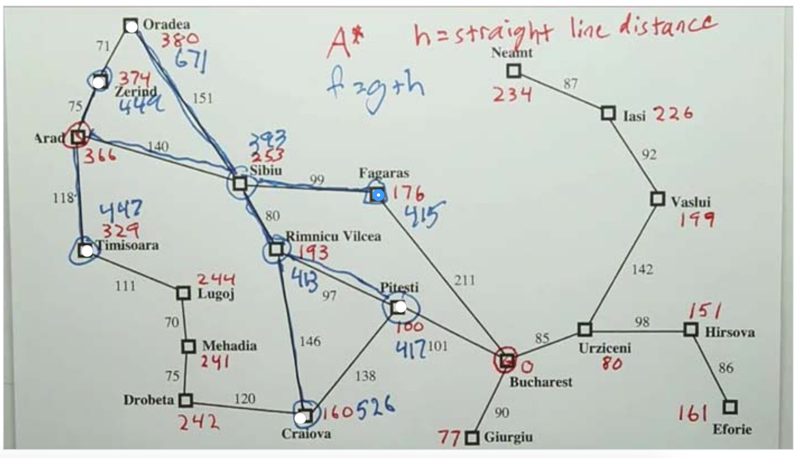
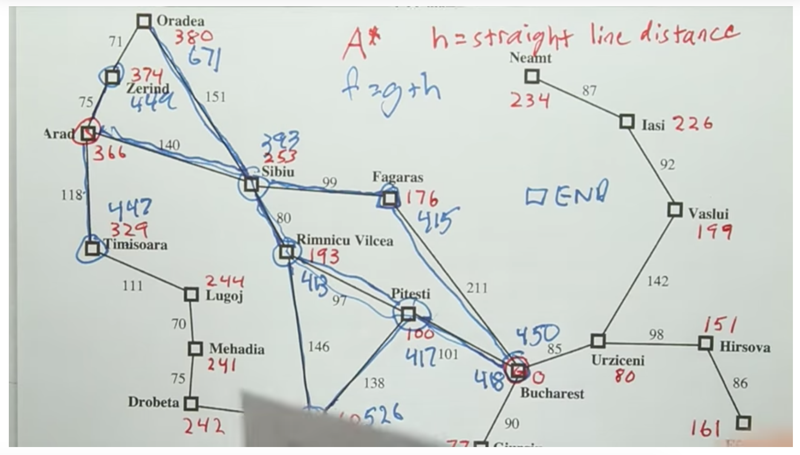
1. The algorithm does not stop when the agent adds the goal state into the frontier, it only finds the shortest path when the goal state was popped out of the frontier.
2. A* finds the optimal paths Will A* always find the optimal?
   • No. In the example above, h always shortens as g increases
   • what if reaching the goal requires both g and h increases?

Optimistic Heuristic

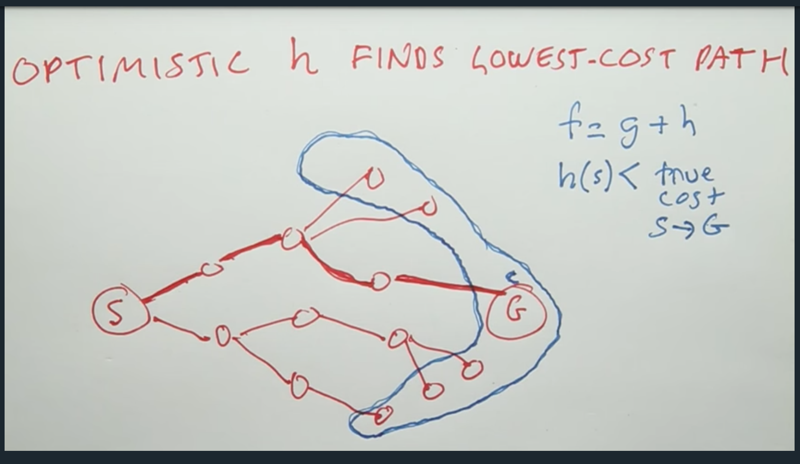
• f(p) < f of other paths since it reached G the first
• h(s) < true cost of S-> G, for the next step, f(s) =g(p)+g(s) -h(s) > f(g), so p will pop the G state out of the frontier, thus ends the search with the path p. (the argument is for tree search)

Vacuum world

Quiz: State Spaces

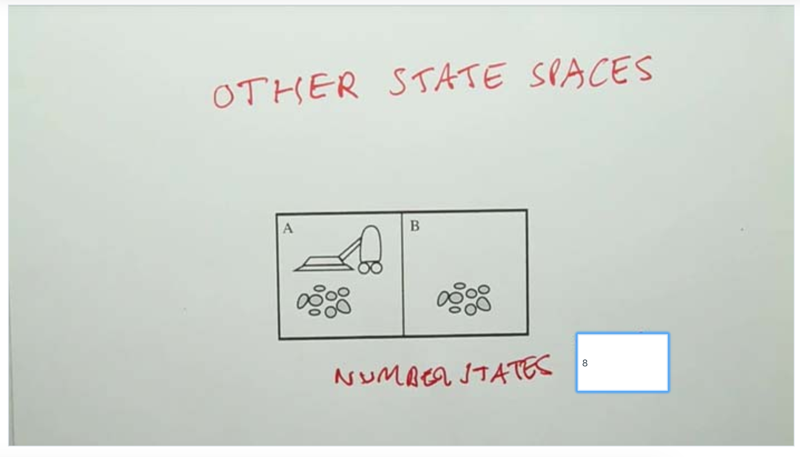
How many states are in the space?

• robot position = 2, cleaness of the position (clean/dirty) 2²
• 2 x 2² = 8

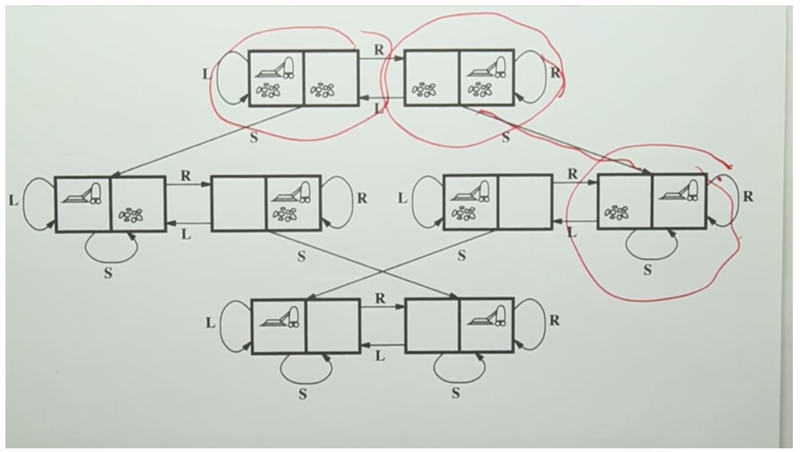
• 3 x 2 x 5 x 10 x 2¹⁰ =307200
• ( here the robot can be in the 10 positions. the 10 positions can have dirt or not (2¹⁰).

Sliding Blocks Puzzle

Which function is admissible? (what is admissible?)

Assume that a move in this game is moving a single block into the empty space (and cannot be a shift of multiple blocks).

• h1 is admissible: each tile in the wrong position must be moved at least once to be in the correct position. it never overestimates
• h2 is admissible: each tile in the wrong position can not move more than 1 blocks
• h2 >= h1

Can the AI come up heuristic functions by itself?

• Where the heuristics can come from?
• loosen the restriction of the problem can generate heuristic
• relaxing restriction equals to adding operators in the problem and make the problem easier but never overestimates, thus, is admissible.

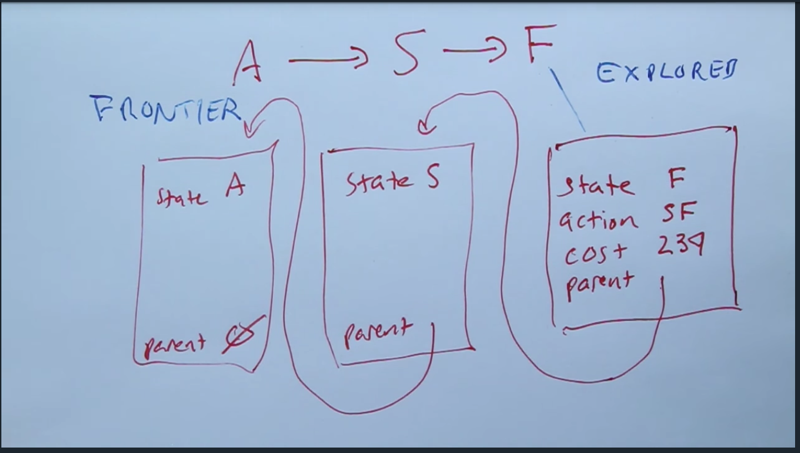
• path is linked nodes by parent pointer.
• Notes can be dealt with data structure Frontier and Explored list
• Frontier: moving best items and add items in the queue; membership check
• Explored list: add new members and membership check. simple set: table or hash table

Readings

• AIMA: Chapters 1-3
• Korf, 1997. Finding Optimal Solutions to Rubik’s Cube Using Pattern Databases. Further Information:
• Goldberg, 2011. Reach for A∗ : An Efficient Point-to-Point Shortest Path Algorithm (slides).
• Goldberg & Harrelson, March 2003. Computing the Shortest Path: A∗ Search Meets Graph Theory.
• Gutman, 2004. Reach-based Routing: A New Approach to Shortest Path Algorithms Optimized for Road Networks.

Challenge Question Revisited

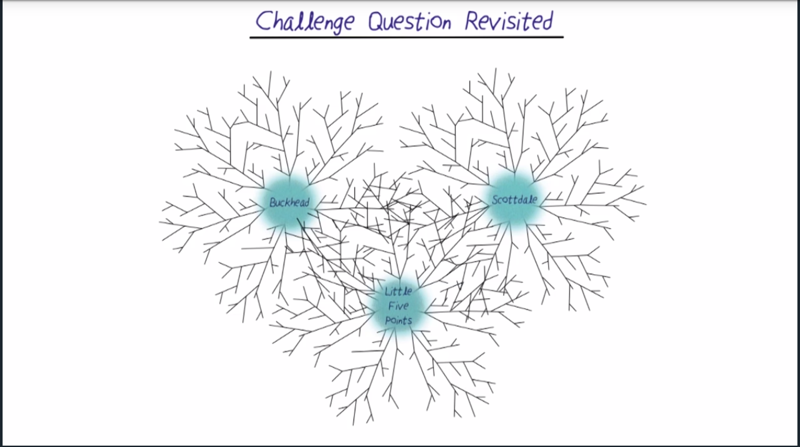
• avoid repeatedly visiting explored notes
• tri-directional search or A* search need to identify an admissible h function

Peter’s Take On AI

Definition of AI: program computer to do the right thing when you don’t know that the right thing is.

20170907 first try, stopped at "sliding block" 150 min
20170908 finished the rest