- Traveling Salesman Problem
- NP hard: Non-deterministic polynomial time
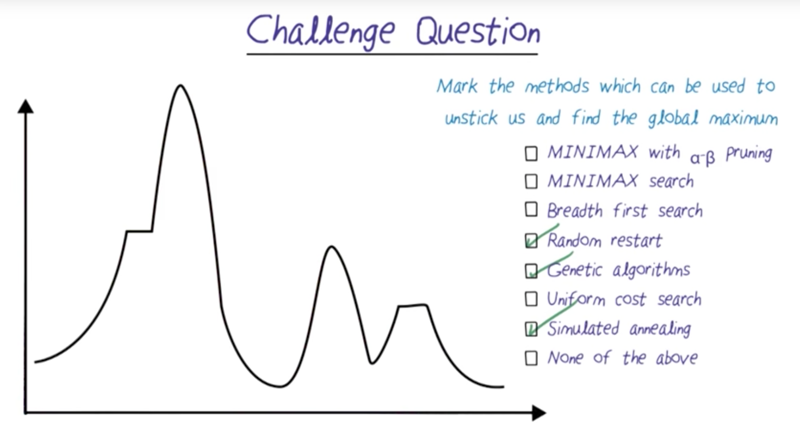
- Quiz: Challenge Question
- 4-Queens
- Hill Climbing
- Annealing
- Genetic Algorithms
This week you should watch Lesson 3, Simulated Annealing, and read Chapter 4 in AIMA (Russell & Norvig).
Assignment 2: Tridirectional Search Due: September 24
Traveling Salesman Problem
NP hard: Non-deterministic polynomial time
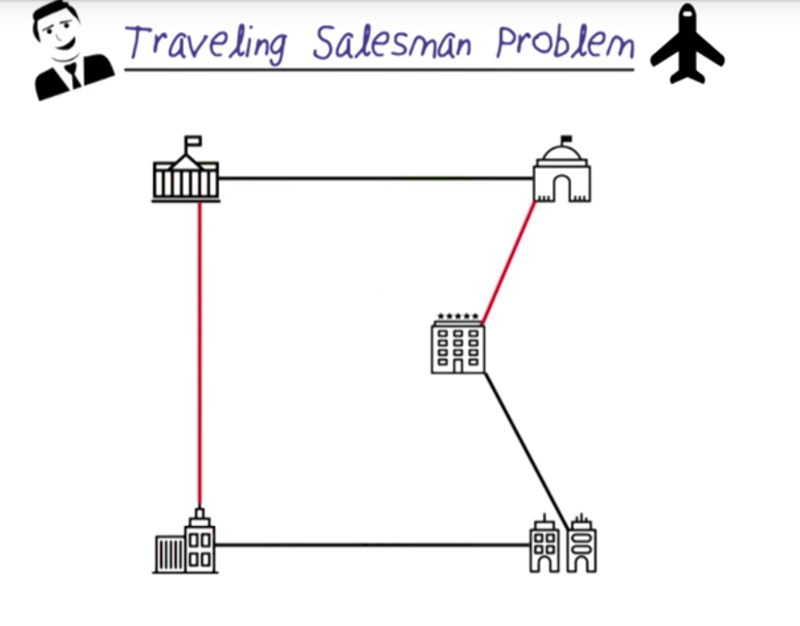
Quiz: Challenge Question
- iterative improvement problem
4-Queens
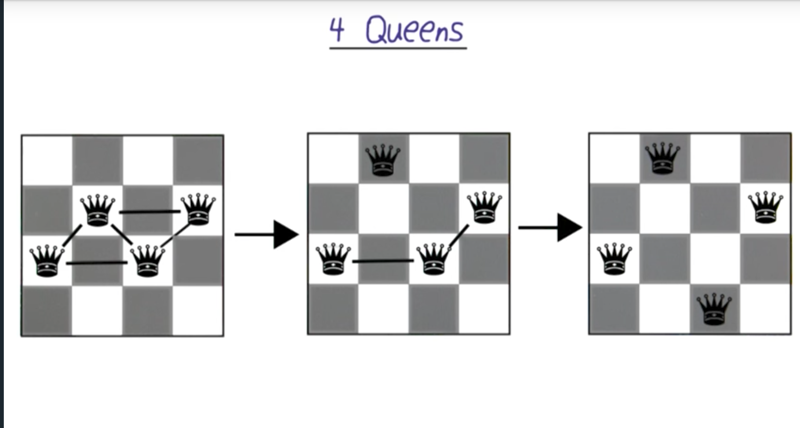
- N-Queens problem: On an N x N board, place N queens.
- Move queens so that they won’t be able to attack one another. That is, no queens on horizontal, vertical or diagonal lines.
- an effective way to solve the problem is to start with the Queen have most attacks and solve it first.

- Note: there are multiple solutions here.
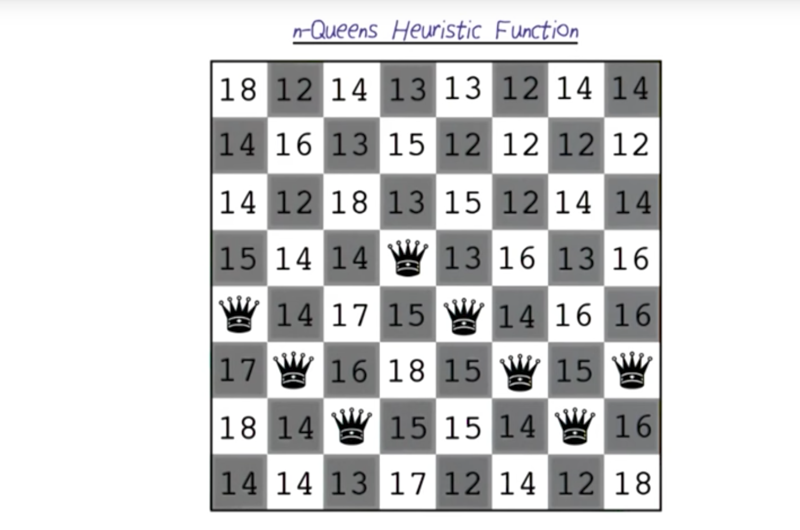
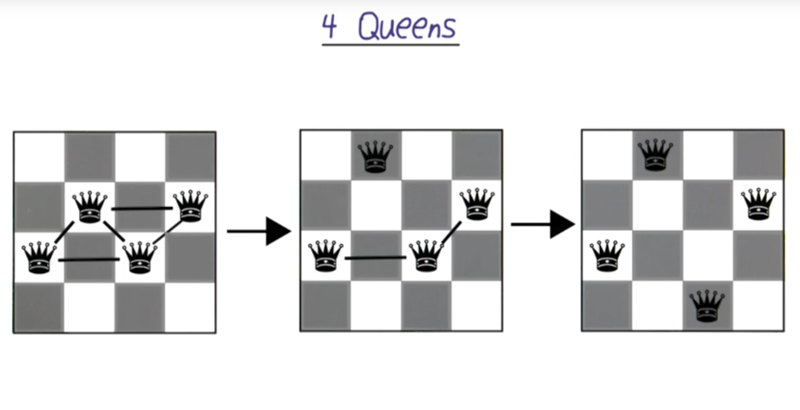
- to solve the question, we can use the “stupid” strategy to take the move to reduce the number of attacks.
- but, it is possible that there would be no move to reduce the number of attacks. See below.
n-queens with local minima

- in the current board above, there is only one attacks happening between the queen in column 4 and 7.
- moving any queen on the board will increase the number of attacks on this board.
Hill Climbing
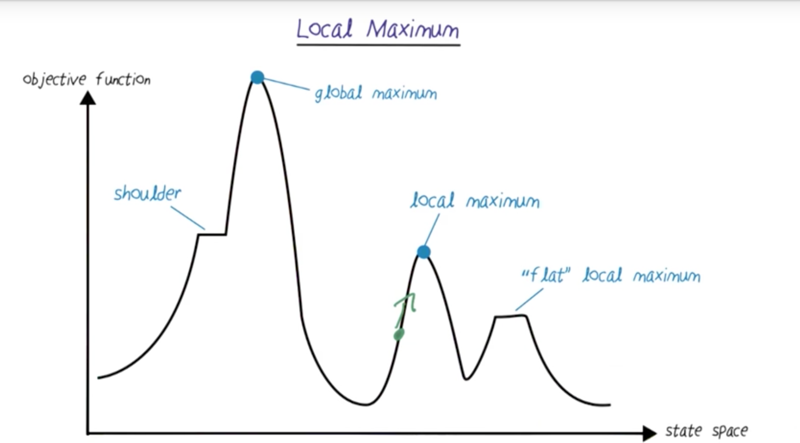
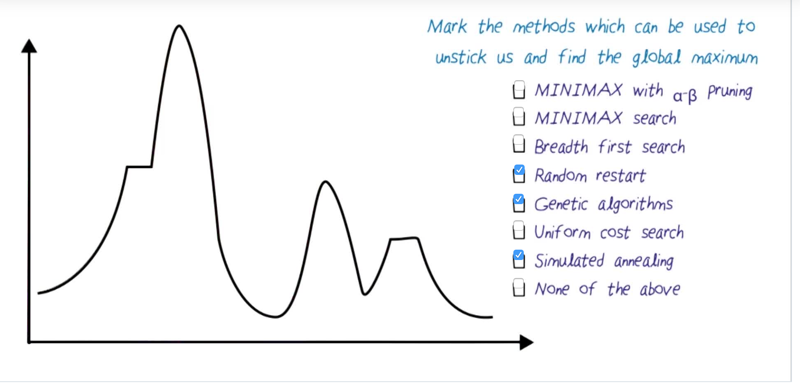
- Goal: to find the global maximum
- method, select a state (initial state), climb the hill to both directions by a small step. The direction that increased the objective function will be chosen for next hill climbing.
- problem: it could get stuck at local maximum ( shoulder, “flat” or pointy local maxima)
- Solution: Random Restart
Random Restart
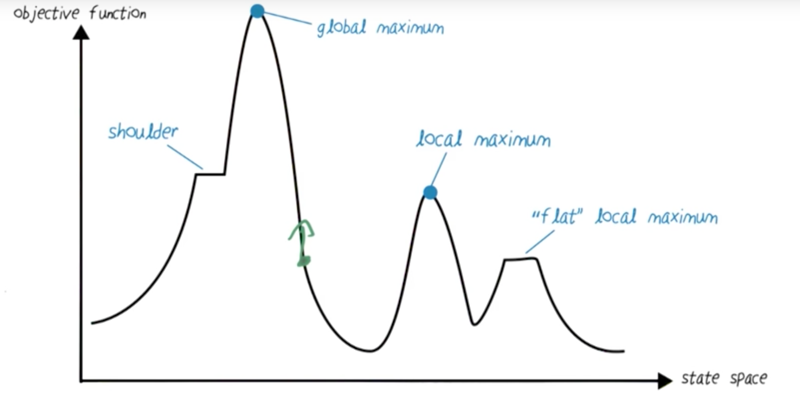
-
we can randomly select a starting point for hill climbing. If we select enough start points of start, then we can find the maximum value and its corresponding state.
- the problem is that we never know if enough sampling was done.
- Taboo search: when randomizing the starting state, use “sampling without replacement”. Once visited, the randomization will not revisit the state visited before.
quiz
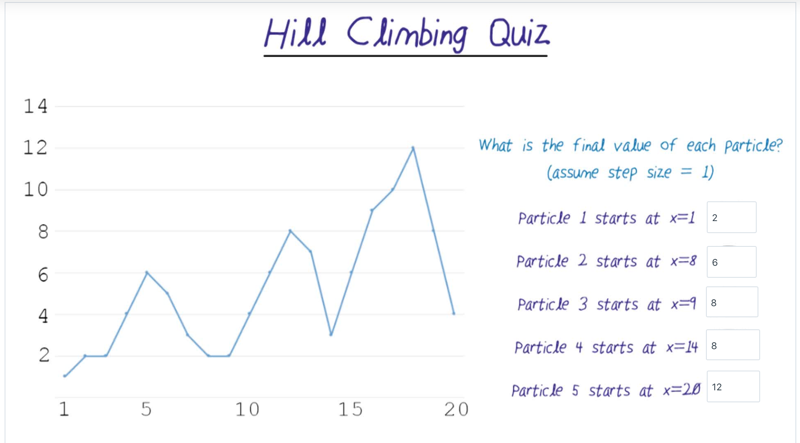
- using hill climbing algorithm, figure out the value of each particle.
step size
- If the step size is small, the algorithm can stick at flat shoulder or maxima.
- If the step size is large, the algorithm might skip the hilltops, ends up oscillating between lower values and never converge.
- solution: start with large steps but end with small steps. Very similar to annealing.
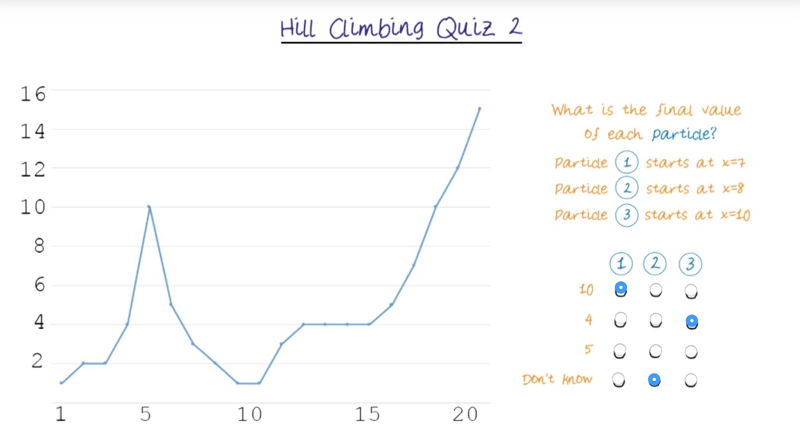
- assuming step size = 2. where each particle will end up with?
Annealing
- In physics, when molecules are allowed to move, they often form structures/patterns to preserve energy, which is minimum energy constructions.
-
Annealing: increase the temperature to allow molecules to move and lower the temperature to let them form new structures until desired structure is achieved.
- Simulated Annealing: heating and cooling idea was borrowed into hill climbing algorithm. The heating means increasing randomness and gradual cooling means decreased randomness. use heating to get out of local maxima and cooling to reach global maxima.
Image sources:
- Mud cracks / sewage sludge - Wikipedia
- Honeycomb - Pixabay
- Columnar basalts - Wikipedia (this one is actually from Iceland)
- Heat treating (atomic lattice) - Wikipedia
- Heat treating (sword making) - Wikipedia
simulated annealing

- T is the simulated temperature at time t, which reduces from a high value at the beginning to near zero eventually.
- ΔE is the change in energy going from current to next.
- when T -> ∞, eΔE / T = e0 = 1 and the simulated annealing allows large randomness, so it can visit a lot of states.
- when T -> 0, say T = 0.01, and the current status have a -1 energy, ΔE = -1. Then eΔE / T = e-1/0.01 = e-100, which is very small and the position will not be taken due to the small posibility.
- when at shoulder or flat maximum, ΔE = 0. no matter what T is, eΔE / T = e0 =1. the algorithm will take a random start to the agent out of the local maxima
Local Beam Search
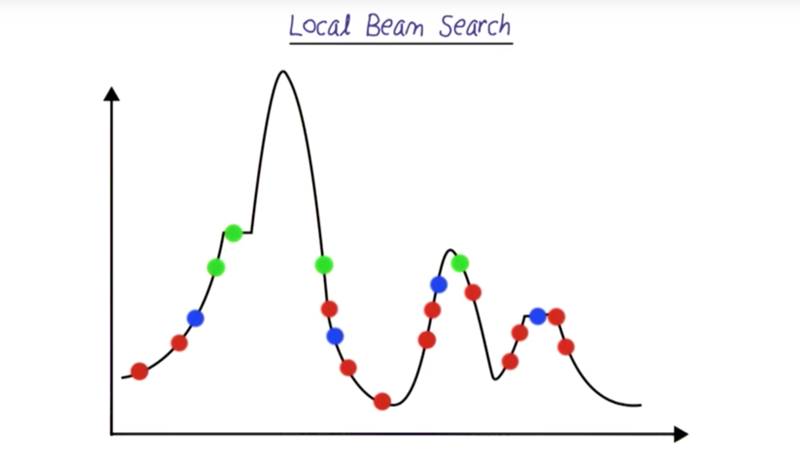
- track multiple particles at the same time
- generate neighbors randomly and compare them to keep the best ones for next iteration.
- stochastic Beam Search: when the generation of neighbors, some randomness was considered when dicide the fitness
Genetic Algorithms
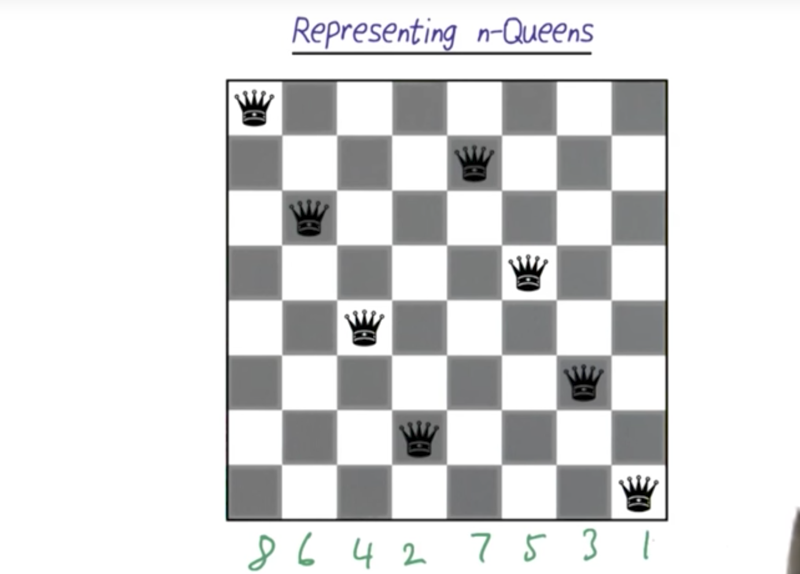
representation N-Queens problem
 the maxim fitness of n-queens problem
the maxim fitness of n-queens problem
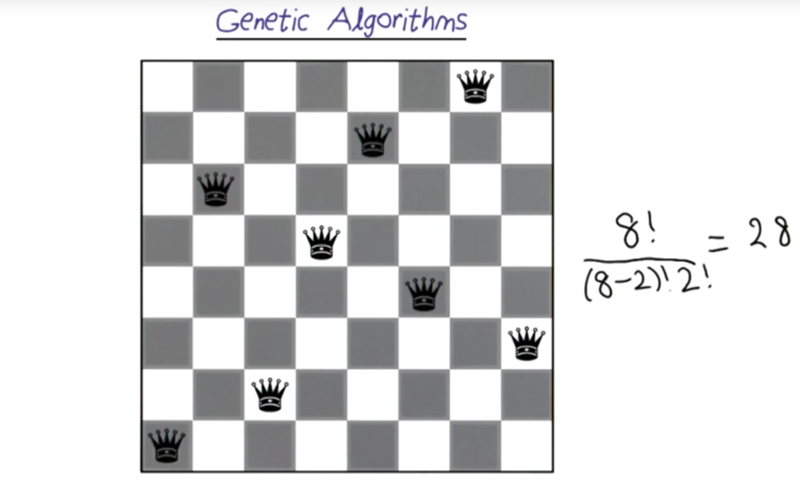
- Maxim number of attaching queens is n!/(n-2)!/2!
- fitness = n!/(n-2)!/2! - # of attacking queens
GA example
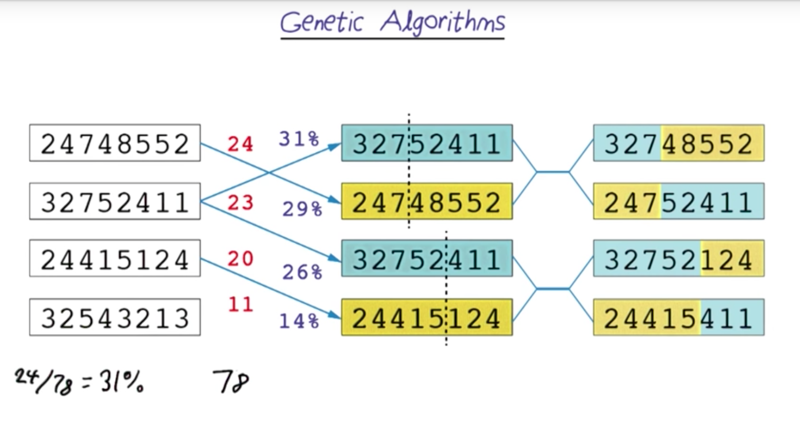
- four random board, first, find their fitness based on the fitness function.
- normalize the fitness value and roll dice of 100 and choose the parent based on the dice #. for example, choose parent 1 when the number is 1 ~ 31, choose parent 2 when the number is 32 ~ 60, and so one…
- when four parents are chosen, children can be generated by crossover, switching part of the sequence with another parent to form a new one. Hopefully, this process will bring the better part of both the parents together.
mutation
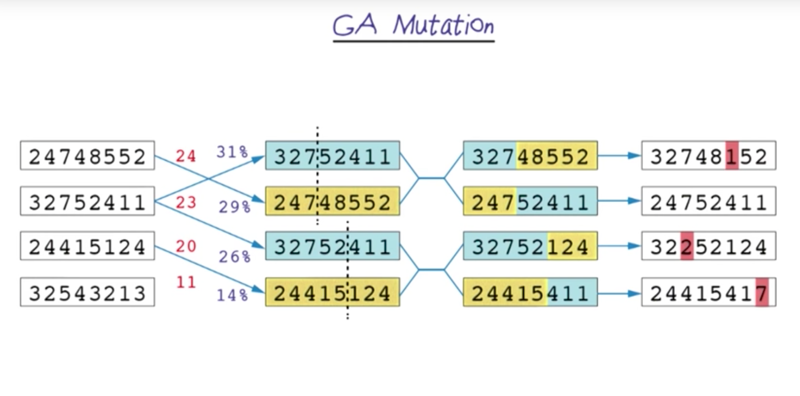
- it’s possible that a critical step is not on any of the parents. In this case, more randomness is needed and one can randomly change one queen’s position.
- The mutation is like to randomly occasionally chose a direction and simulated annealing while the randomness part is more like sochastic beam search.
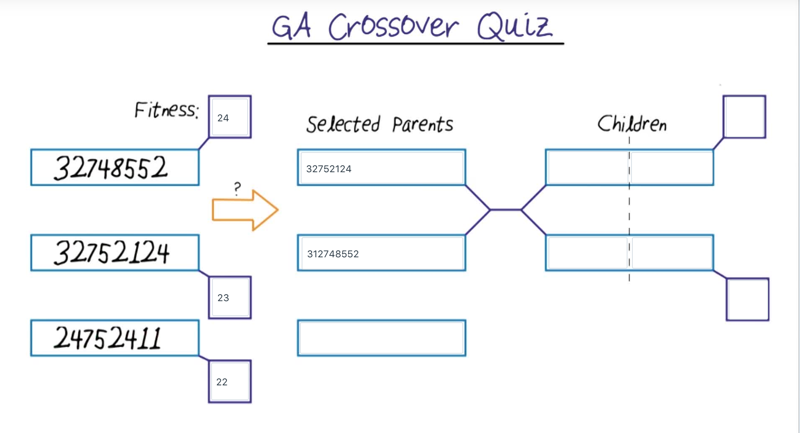
GA quiz
challenge question revisited
For another viewpoint and some extensions, check out Charles Isbell and Michael Littman’s course section on this topic: Randomized Optimization
20170917 - v01: 3 hours