• 01 - What is an optimizer
• 02 - Minimization example
• 03 - Minimizer in Python
• 04 - Quiz: How to defeat a minimizer
• 05 - Convex problems
• 6 - Building a parameterized model
• 07 - quiz What is a good error metric
• 08 - Minimizer finds coefficients
• 09 - Fit a line to given data points
• 10 - And it works for polynomials too
• 13 - Wrapping up optimizers

01 - What is an optimizer

What is an optimizer?: An optimizer is an algorithm that can:

• find minimum values for functions.
• find the parameters for parameterized models from data.
• find a polynomial fit to that data.
• refine allocations to stocks in portfolios (e.g. what percentage of funds should be allocated to each stock).

How do we use an optimizer? three key steps.

1. define a function that you want to minimize. define in Python and then the minimizer will call this function many, many times as it tries to find the minimum values for x that causes this function overall to be smallest.
2. Choose an initial guess for x (might be close to the solution to the problem or choose a random value, or just some standard value).
3. call the optimizer starts with that guess and it repeatedly calls a function, tests different values, and narrows in on the solution.

Time: 00:02:30

02 - Minimization example

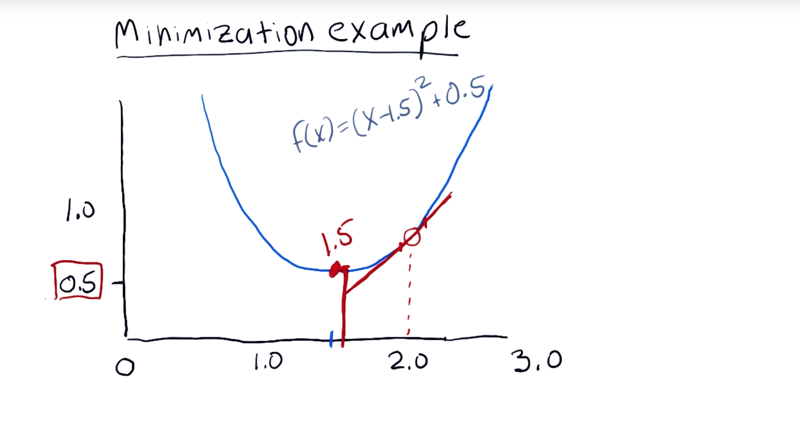
• example: f(x) = (x - 1.5)² + 0.5. The function is centered horizontally at 1.5, and its minima is here at 0.5.

• for example, the optimizer start with a guess of 2.0.
• The first thing it does is it checks the value at 2.0, it turns out that that’s about 0.75. then tests the value nearby and finds out that this equation’s slope
• Now, it’s trying to minimize, and it marches downhill, it’s called gradient descent
• Eventually, it narrows and it discovers that 1.5 is the value for x at the minima and the value of y there is 0.5.
• And SciPy, the library that we’re using, has many of those options.

Time: 00:02:10

03 - Minimizer in Python

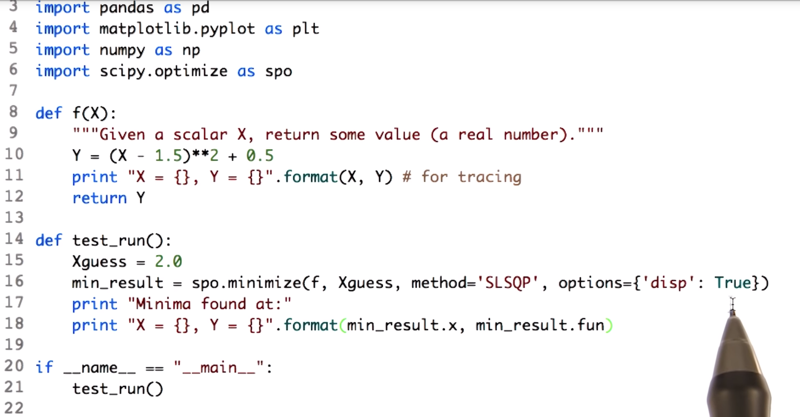
• Function to minimize Y= (X-1.5)**2 +0.5.
• import scipy.ptimizer as spo
• spo.minimize(f,Xguess, method='SLSQP', options={'disp': True}) call the optimizer or the minimizer by setting the guess value to be 2.0.
  • F is the function here, so we’re saying minimizer,
  • Method is the minimizing algorithm.
  • disp is True, which means “verbose about things that it discovers”.
• The minimizer repeatedly calls our function and finds the minimum value

Let’s try a test run and see what happens.

• the minimizer is repeatedly calling that function f and it’s printing these things out.
• When X = 2 and it discovers that the value is 0.75.
• Then a value slightly greater than 2, a value slightly less than 2.
• And the minimizer very quickly converges on 1.5 as the answer with a value of 0.5 .

Time: 00:03:25

04 - Quiz: How to defeat a minimizer

Given the four function shapes to look at, which one(s) is harder to sovle and why?

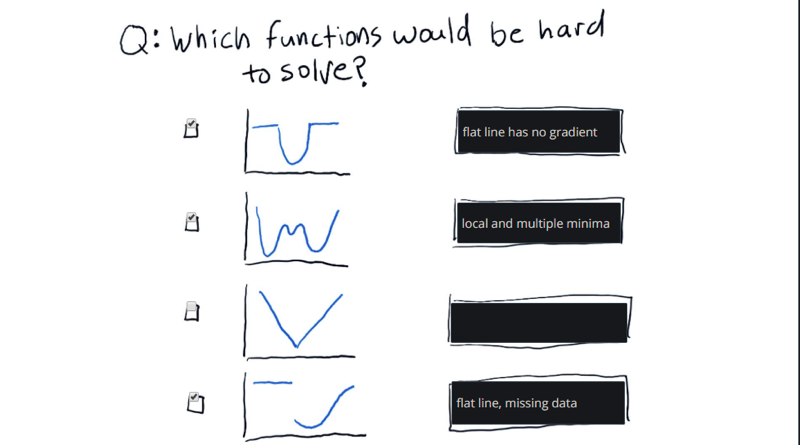
Note: these are solvable by optimizers, but just hard. In fact, there are optimizers that can solve these problems with varying degrees of success. but sucess is not guareentted.

Time: 00:01:30

05 - Convex problems

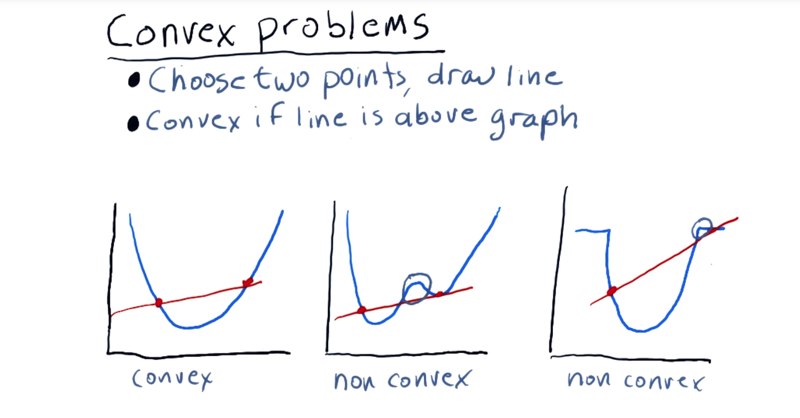
Minimizer are especially good at solving convex problems.

The formal definition of a convex function.

A real valued function f(x) defined on an interval is called convex if the line segment between any two points on the graph of the function lies above the graph.

To tell if a function is vonvex:

1. choose two points and draw a line between them.
2. for each of these lines, if the line is above the graph, everywhere between those two points, then the function is convex between those points.

• In order for the function to be convex, 1) it has to have only one local minima.2) it can’t have any flat regions that essentially don’t have any slope downward.
• Non-convex problems might be solvable they require a little bit of randomness and they aren’t necessarily guaranteed to find the global minima.

Time: 00:03:10

6 - Building a parameterized model

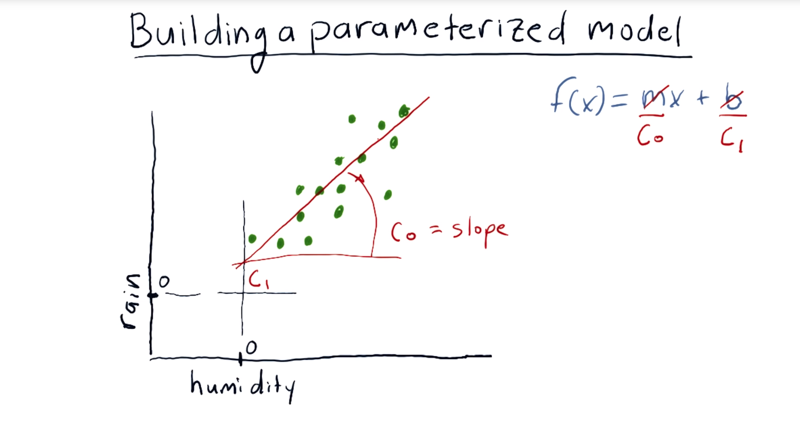
• parameterized model, for example, used parameters to represent slop and intercept in a function f(x) = C₀x + C₁. C₀ and C₁ are parameters of the linear model.

• Suppose we have a data set represented by the green dots, if we fit the data by a line, it looks like the line will have is C₀ equivalent to the slope here, and C₁ is the y intercept.

• Suppose this blue line is a candidate line and we want to evaluate it. Is this good or bad?

  • a minimizer can vary C₀ and C₁ to try and minimize something to come up with an equation that gets lower in value as this line better fits the data.

What should we use for that equation?

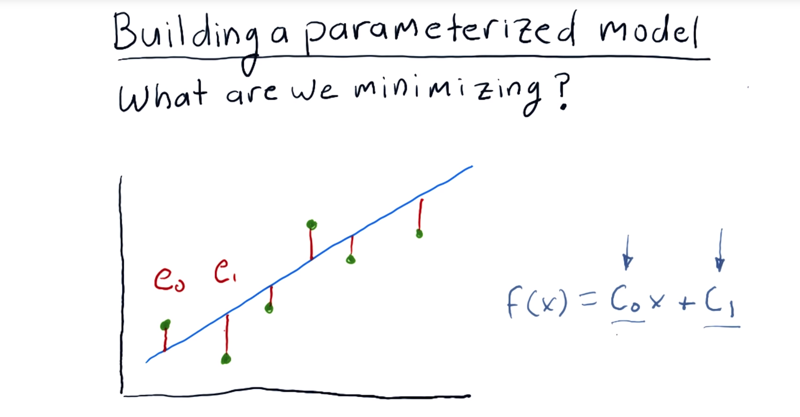
• error: each one of our original data points and observe how far away it is from this line that we’re evaluating.

Time: 00:03:31

07 - quiz What is a good error metric

__ which of these formulae might be a good overall error measure?__

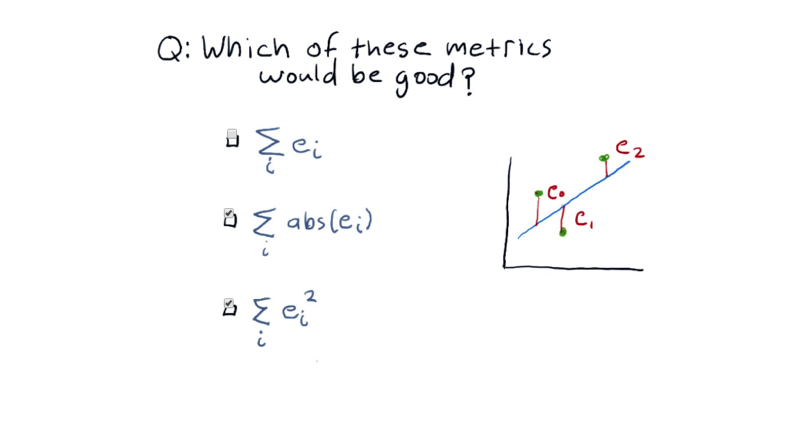
Simply summing up the errors doesn’t work, as some of them may be negative. Taking the absolute value or squared error solves that problem.

08 - Minimizer finds coefficients

Steps of a minimizer finding the coefficients of a line that best fits this data. (we need to give the minimizer an equation that it has to minimize).

• the function to minimize is the error metric function, in this case, the squared error.
  1. guess an initial C₀ and C₁ and that would be a line like this, and we would give that to the minimizer and let it go.
  2. the minimizer would measure the error with this particular line, it would fiddle with these values a little bit and see how much the error changed, try a new set of values see how that works.
  3. it’s going to iterate, and eventually settle on what it thinks is the best solution.
• key points here are that we express the problem for the minimizer as a minimization problem and we give it the equation to minimize as the error.

Time: 00:01:16

09 - Fit a line to given data points

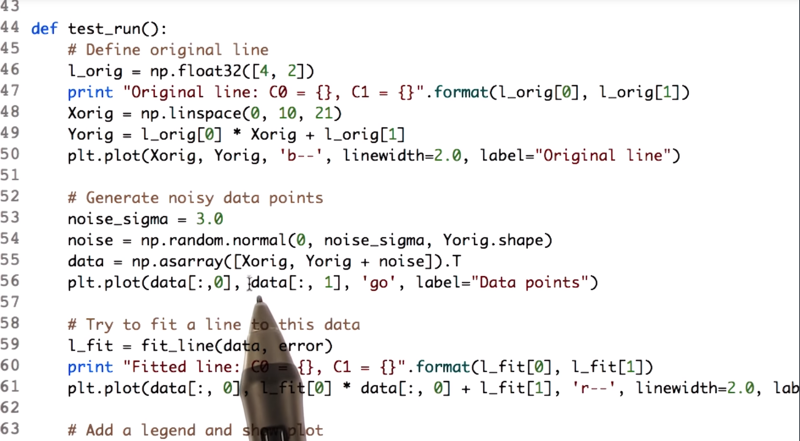
• in the test_run() function, we plot the original line (ln 45~50), add some noise to the data (ln 52~ 36) and fit the line with the the fit_line(data, error) function and data and error function as input.
• the error() function and the fit_line() are defined by the code below.

• function error(), and it takes two parameters, line and data. Line is just the two coefficients, C₀ and C₁. And data is just a list of data
• ln20: err is the squared error which is the squred difference between the data and the estimated data by the line.

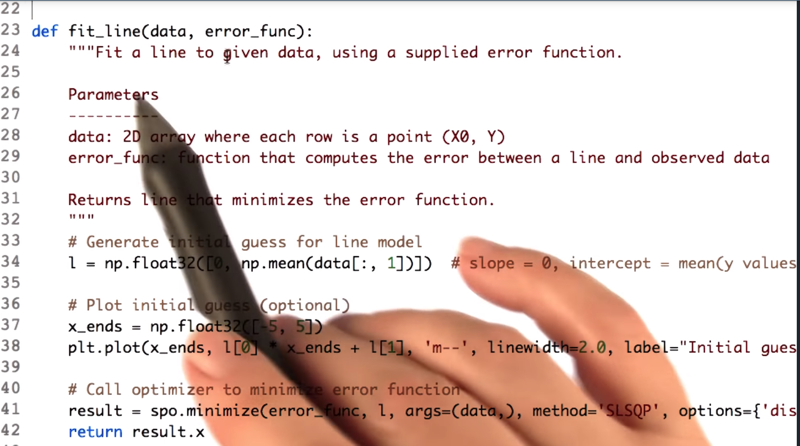
• ln 34 is the inital value for the linear model. here we set the splot to be 0 and the Y-intercept is the mean of the y value of all the datapoints.
• ln 37 is the range of X
• ln 41 calls the minimizer, give it the error_func, ininital guess l. args=(data,) passes the data into the error function.

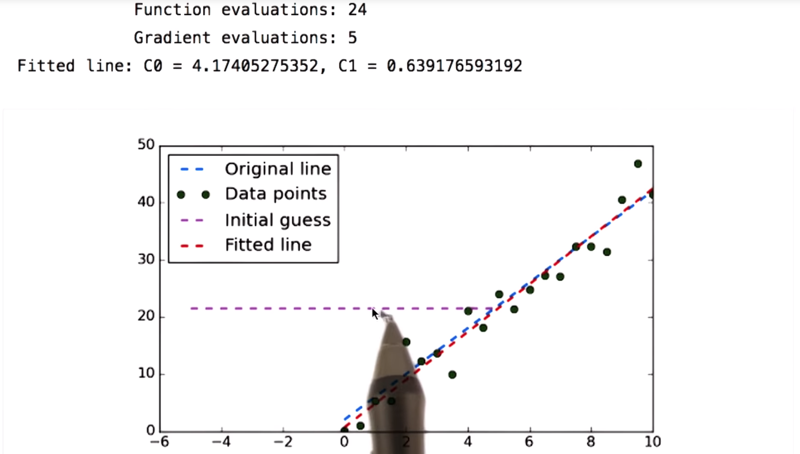
• Our original line is this blue line.
• These green dots are our noisy data where we just added noise values to the blue line.
• What we did were
  • asking our optimizer to find the equation of a line that best fits this data.
  • The metric we are trying to minimize is error.
  • we passed it in an initial guess (purple line) and the noisy data.
• the minimizer iterates and tries different slopes and different y intercepts. Until finally, it converges to the red line and that’s the solution.

Time: 00:05:51

10 - And it works for polynomials too

We can fit even more complicated functions to data like this.

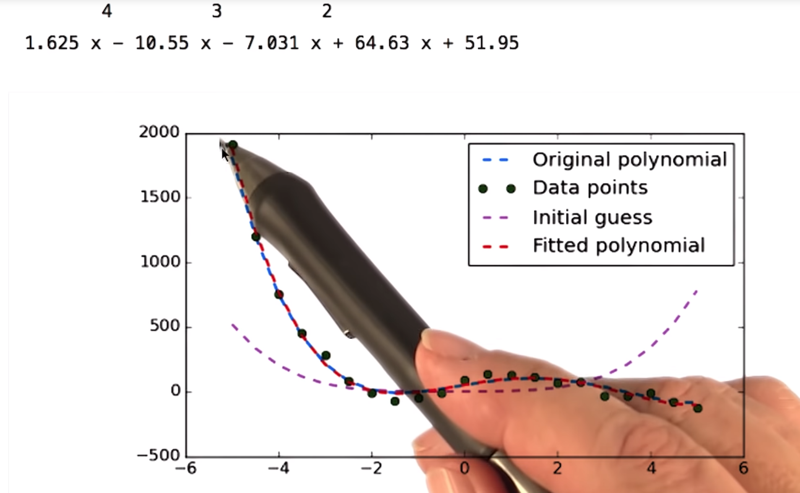
Our original polynomial is f(x) = 1.5x⁴ - 10x ³ - 5 x²+ 60x + 50.

Let’s look now at how we do that in code.

• a higher-degree polynomial is very similar to what we had for the line.
• take in the coefficients for the polynomial and the actual data.
• ln 20 is the error function, it’s a sum of the difference between the actual data and the polynomial value squared and we take the sum of all those values as error metric.

Here’s our function that finds the coefficients of the polynomial has just a few parameters.

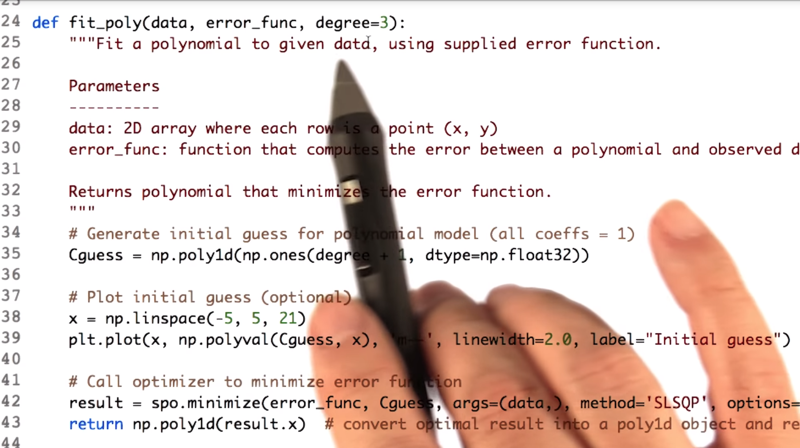
• the fit_poly() function will take the data and trying to fit our error function. And the degree of the polynomial.
• ln 35: We created an initial guess. setting them all to be ones.
• ln 38~39: plot that,
• line 42:we call our minimizer.

And that’s it that’s how we use Python to create a model based on data.

Time: 00:03:07

13 - Wrapping up optimizers

Recap: We have learned

• how to use a minimizer to find x such that f of x is minimized.
• how to minimize in multiple dimensions.
• how to use a minimizer to build a parametrized model.

Where can you go from here?.

• You can use functions besides polynomials, you can model stock prices, or you can optimize a portfolio.

Time: 00:00:27

Total Time: 00:28:37

2018-01-15 初稿