This week you should do Lesson 9, Logic & Planning , and read Chapters 7-10 in Russell & Norvig. Additional readings can be found on the course schedule.

Readings on Logic and Planning. AIMA: Chapter 7-10 (Logic), Chapter 11-12 (Planning)

Introduction

AI to be the study and process of finding appropriate actions for an agent.
So far we search over a state space based on a problem description to find a solution, a path to the goal.
But they only work for deterministic and fully observable problems.
In this unit, we will see how to relax those constraints.

Intro to Logic and Planning

A logic is a way of describing the world.
The description is only partial: Logical statements capture part of the world and ignore other parts.
Once we’ve made some statements about the world, we can then reason completely within the logic to come to some conclusions. if original statements correctly represent the world, so too will the conclusions be correct.

Situation Calculus

Initial state S₀ and goal state S can be expressed by language in the ordinary language of first-order logic.
The advantage of situation calculus is that we have the full power of first-order logic, much more flexible than problem solving or classical planning ( what are they?)
The weakness in all these different approaches is that we weren’t able to distinguish between probable and improbable solutions.

Background and Expert Systems

historical perspective on the topic:

AI started with the idea coming up better languages and systems for writing down logical statements. and use logic to solve all problems. Result: Some worked great but others failed.
Issues that cause failing: 1) make statements only in Boolean logic; 2) writing all statement by hand.
solution: 1) introducing probability to deal with the uncertainty of the world; 2) learning about the world from data.
And still logic has its place.

How is logic used today?

A: Eliminating much of the uncertainty of the real world and solving significant problems using logic. E.g., FedEx planning all the deliveries of its packages using its huge fleet of vehicles.

Expert systems
Logical representations to planning algorithms for when actions or even the world is uncertain.

What directions do you think we will be seeing for planning algorithms in the future?

A: 1) learning from examples would be an important area. 2) Transfer learning across domains, 3) interactive planning.

In this section, we will cover:

1) the resolution algorithm, an elegant way of inferring new knowledge from a knowledge base. 2) Graphplan, and 3) value iteration, which is a key concept for Markov decision processing.

Intro to Logic

How AI managing complexity and uncertainty？

search can discover sequences of actions to solve problems.
probability theory can represent in reason with uncertainty.
machine learning can be used to learn and improve.
In agent design: simple reflex-based agent and move into goal-based and utility-based agents.
the complexity of the environment: simple environments to partial observability, stochastic actions at multiple agents, and so on.
representation, the agents model of the world becomes increasingly complex.

This unit will concentrate on that third aspect of representation, showing how the tools of logic can be used by an agent to better model the world.

Propositional Logic

How to write logic statement

Propositional symbols B, E, A, M, and J corresponding to (B)urglary occurring, (E)arthquake occurring, (A)larm going off, (M)ary calling, and (J)ohn calling. This is the example used in the probabalistic models.
Logical sentences: 1) (E V B) => A reads E or B implies A, which means that alarm is true whenever the earthquake or burglary is true. 2) A => (J ^ M) reads A implies J and M. 3) J <=> M. John is equivalent to Mary–when one is true, the other is true; when one is false, the other is false. 4) J<=> - Mary, J is equivalent to not Mary
A propositional logic sentence is either true or false with respect to a model of the world.
A model is just a set of true/false values for all the propositional symbols.

Truth table

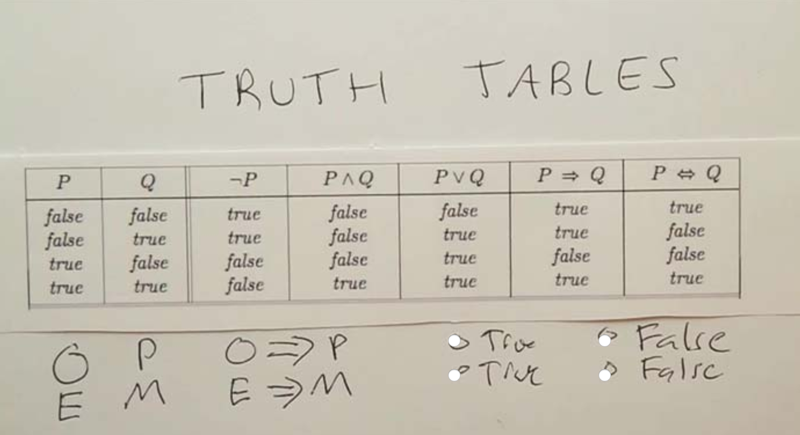
Truth tables list all the possibilities for the propositional symbols
“or” means either or both.
P => Q, P implies Q; or as if P, then Q. Note: the meaning in logic is defined explicitly by this truth table and nothing else.
Quiz: the proposition O means Five is an odd number and P meaning Paris is the capital of France. what is O => P? (when P is True and Q is True, P => Q is True)
If E is the proposition that five is an even number and M is the proposition that Moscow is the capital of France, what about E => M? (when P is False and Q is False, P => Q is True)

Truth Table Question

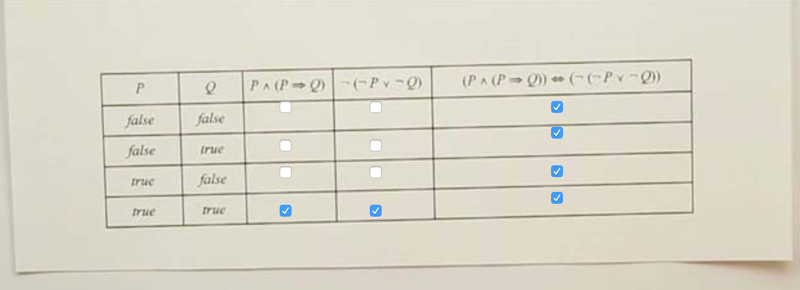
Given the truth table above, choose the box where the proposition sentence is True Answer to the Truth Table Question

P ^ (P => Q) are only true when P and Q both are True.
- (P v -Q) is only True when P and Q are both True.
and they agree with each other all the time, so the last column should be all selected.

Quiz: Propositional Logic Question

In a particular model of the world, we know the following sentences are true. (E V B) => A, A => (J ^ M), and B. Of the propositional symbols, is that symbol true or false, or unknown in this model?

Answer to the Propositional Logic Question

B is True, thus (E v B) is True, thus A must be True
SInce A is True, thus (J ^ M) is True, this means J and M must be True at the same time to make the second statment correct.

Terminology

Valid sentence is one that is true in every possible model, for every combination of values of the propositional symbols.
Satisfiable sentence is one that is true in some models but not necessarily in all the models.
So, for each of these sentences, whether it is valid, satisfiable but not valid, or unsatisfiable, in other words, false for all models.

Answer to the valid and satisfiable models

The first four are easy to understand, just look at the Tureth table to get the answers.
the last one, Food => Party is False, Drinks => party is also False, so ((Food => Party) V (Drinks => party) is False. According to the Truth table, when P is False P => Q is True, no matter what Q is. Here ((Food ^ Drink)=> party) is Q.

Propositional Logic Limitations

Propositional logic is very efficient inference mechanisms for determining validity and satisfiability, although we haven’t discussed them.
First, it can only handle Boolean values. Cannot handle uncertainty
Second, Can’t talk about objects that have properties, (e.g., size, weight, color…) or relations between objects.
And third, there are no shortcuts to succinctly talk about a lot of different things happening.

First-Order Logic

The content of the part: first-order logic and its relation to the other logics ( propositional logic and probability theory).
1) what they say about the world, which we call the ontological commitment of these logics; 2) what types of beliefs agents can have using these logics, which we call the epistemological commitments.

World and belief

Logics vary both in what you can say about the world and what you can believe about what’s been said about the world.

Logic	World	Belief
first order logic	relations about things in the world, objects, and functions on those objects.	true or false or unknown.
Propositional logic	facts	facts are true or false or unknown
Probability theory	facts (the symbols or variables)	real number {0, 1}

Another way to look at representation is to break the world up into representations
- Atomic, meaning that a representation of the state is just an individual state with no internal structure to those states.
- Factored representation– a state of the world is factored into several variables: (Boolean variables or on non-Boolean)
- Structured representation. Variables, and relationships between objects, (a branching structure, and complex representations and relations between objects)

How does first-order logic work? What does it do?

Models

Model in First-order logic

In propositional logic a model was a value for each propositional symbol.
In first-order logic, the models are more complex.
- a set of objects. Here I’ve shown objects
- a set of constants that refer to those objects. A, B, C, D, 1, 2, 3. (Note, the constant names could be different than objects)
- a set of functions. A function is defined as a mapping from objects to objects. E.g.: Number Of function
- Relations. E.g., Above relation, unary relation (vowel), Rainy (which doesn’t refer to any objects, can be represented by an empty set or a set of the empty list)

Syntax

Sentences: which describe facts that are true or false.
- atomic sentences
- the equality relation (the equality relation is always in every model)
Terms which describe objects. Can be constants, variables, and functions.
Operators:
- sentences can be combined with all the operators from propositional logic: and (^), or (V), not (-), implies(=>), equivalent(<=>)
Quantifiers are complex sentences that make first-order logic unique.
- Two quantifiers: For all (upside-down A), and there exists (upside-down E)
- sometimes we’ll omit the quantifier

Vaccum world

Vacuum World

terms: left location A and the right location B and the vacuum V, and the dirt–say, D1 and D2.
Relations: loc, which is true of any location; vacuum, which is true of the vacuum; Dirt, which is true of dirt; and At, which is true of an object and a location.
- so if the vacuum is at location A, we just say At(V, A). *No dirt in any location
“First order” means that the relations are on objects, but not on relations.
A notion of a transitive relation talking about relations itself is valid In higher-order logic, but invalid in first-order logic

Quiz: FOL Question

For each sentences, tell if it is 1) valid: O is true; 2)satisfiable, but not valid: that is, there’s some models for which it is true; or 3) unsatisfiable: there are no models for which it is true.

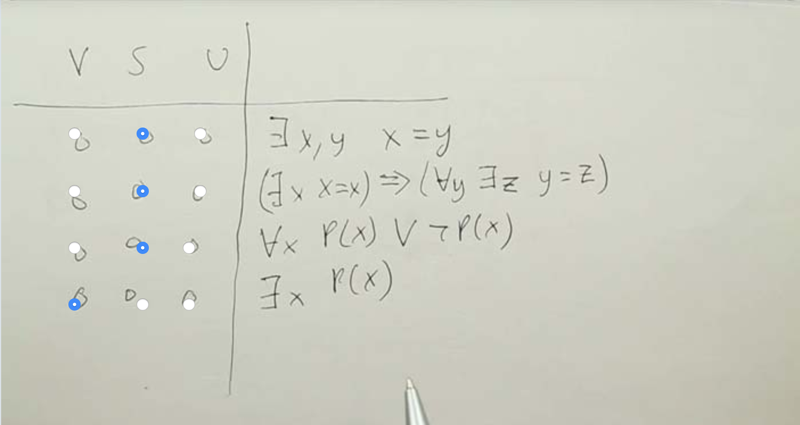
First sentence: is valid. Because every model has to have at least 1 object and we can have both x and y refer to that same object
Second sentence:The left-hand side is true. The right-hand side is true, similar to the sentence above.
Third sentence: Valid.
The fourth: Satisfiable. it’s true for the models in which there is some x that is a member of P. it’s false when P is an empty relation, so this is satisfiable.

FOL Question 2

Can the sentences represents: 1) “Sam has 2 jobs,” 2) I want to represent the idea of set membership. And 3), define the notion of adjacent squares on, say, a checkerboard, where the squares are numbered with x and y coordinates and we want to just talk about adjacency in the horizontal and vertical direction.

Answer: the first one is but the second and third ones are not. Both the second and the third are incomplete. Second defines what is a member but did not define what is not. The third only defined adjacency in one direction.

Planning

Problem Solving Vs Planning

Problem-solving works as: in a state space, PS agent searches a path from start space to a goal and then it starts to execute that path.
But in real life, execution without interacting with the world will often fail.
The moral is we need some feedback from the environment and interleave planning and executing.

Planning Vs Execution

Now why do we have to interleave planning and execution?

the environment is stochastic.
multi-agent environments.
partial observability.
some model of the world is unknown (inaccurate sensor),
the plans have to be hierarchical. When low-level steps of the plan aren’t sketched out in detail but only have the high-level parts of the plan. Solution: Instead of planning in the space of world states, we plan in the space of belief states.

Vacuum Cleaner Example

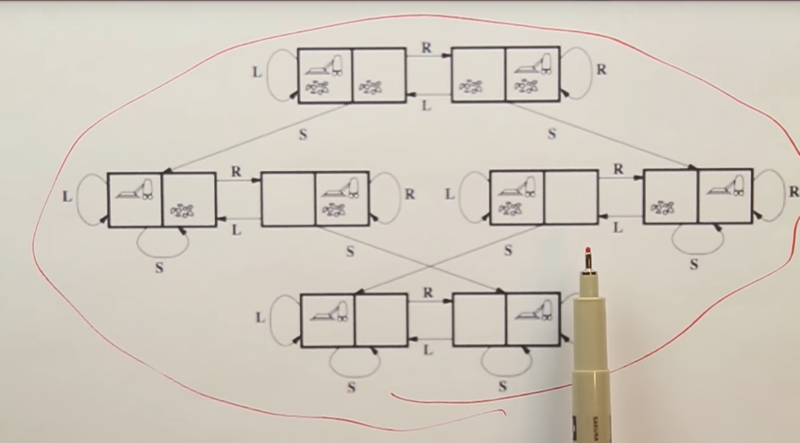
State space diagram: a room with 2 locations(A, and B), a vacuum cleaner, and dirt, and so that gives us 8 total states. 3 possible actions (moving right, moving left, and sucking up dirt)

if we have a fully deterministic, fully observable world, it’s easy to plan.
Let make the world unobservable: suppose our robot vacuum can no longer perceive location or dirt. So we believe that we’re in 1 of these 8 states, and now when we execute an action, we’re going to get to another belief state.

Sensorless Vacumm Cleaner Problem

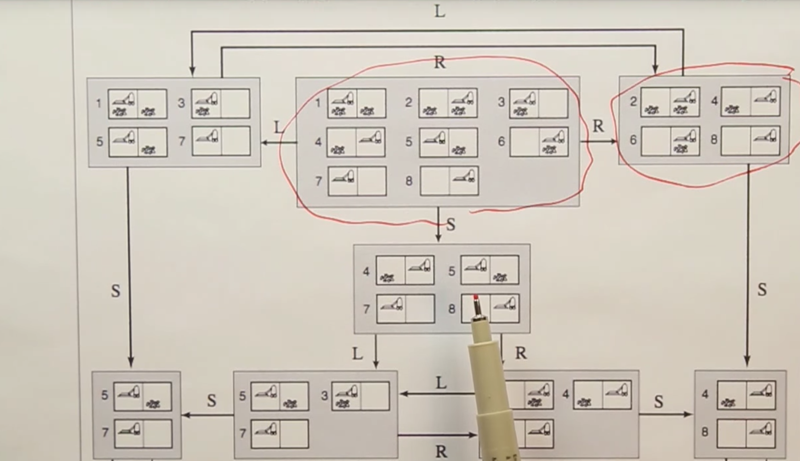
belief states: contain multiple possible states. but if we execute actions, we can gain knowledge about the world even without sensing. E.g.: moving right will take the robot to the right-hand location; sucking can make the current location clear.
in the belief state world going right and going left are not inverses.
it’s possible to form a plan that reaches a goal without ever observing the world. they are conform-it plans.
quiz question, How to get from the state my current square is clean, but know nothing else, to the belief state where I know that I’m in the right-hand side location and that that location is clean?

Partially Observable Vacuum Cleaner Example (still in a deterministic world)

Partially observable planning in a deterministic world. we have local sensing (can sense current location only).
act precept cycle
- Taking action won’t change the number of worlds in belief state.
- Observation, can split that world into two believe states.

Stochastic Environment Problem

quize

stochastic environments. slippery wheels: the Left or Right action is not always successful. The suck action works perfectly. Observation works so it can split believe state.
quiz questions, how to get to a state where all the squares are clean from the left root state.
Answer: all plan might reach the goal but it is not guaranteed.

Infinite Sequences

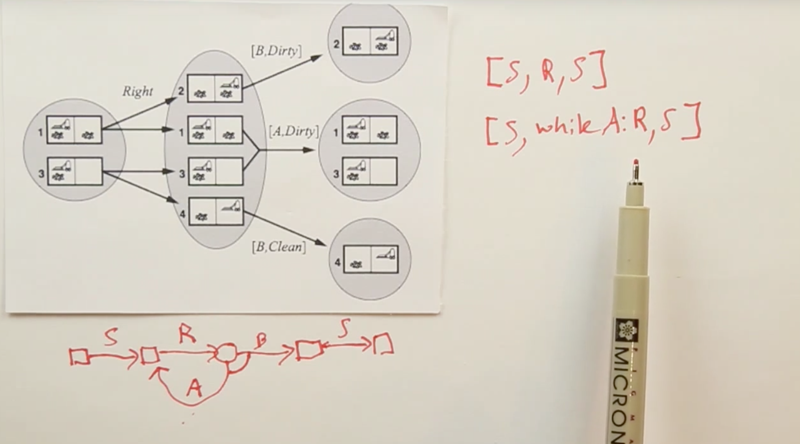Continue with the example above, if we observe after the move action, and if the location is not changed after the “Right” action, it will repeat the action, until we observe the location is successfully changed. Then we suck. this uses finite symbols to represent an infinite sequence of action. It guaranteed success but we don’t know how many steps the process will take.

Finding A Successful Plan

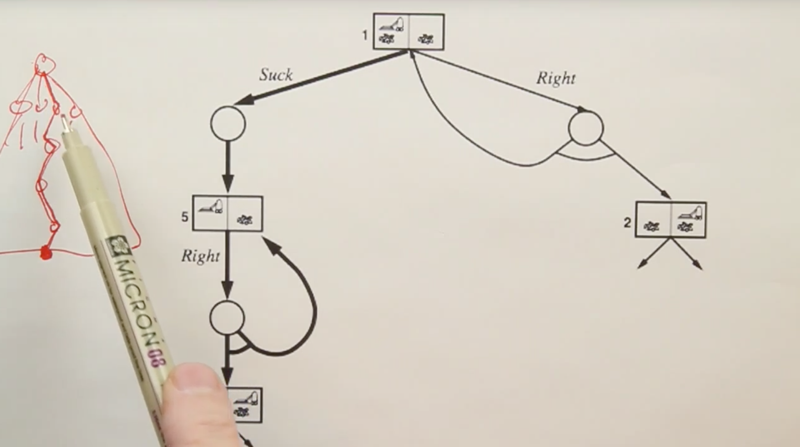
The process to find a plan is to establish a tree structure of the sequence and do a search from the start state to the target state.

Problem Solving Via Mathematical Notation

We could use Mathematical Notation to see if a sequence of questions can lead to goals.

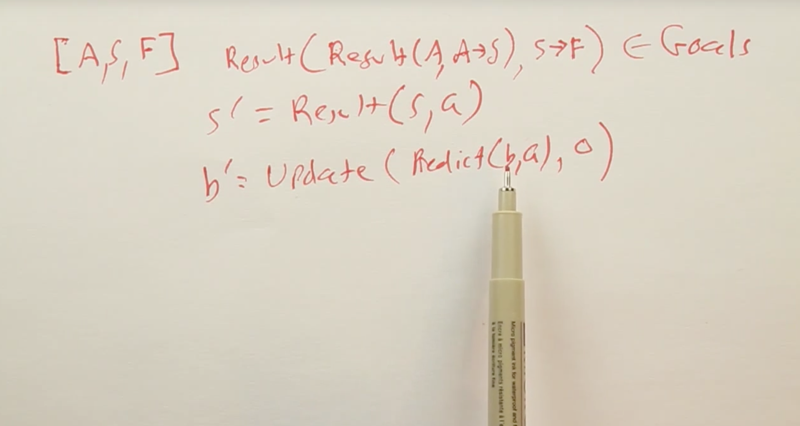
s' = result(s,a) means the result of agent in state s and take action a is the agent ends up in a new state s'
b' = update(predict(b,a),o) means that given the current believe state b and agent’s action a , and then update the knowlege of the targe state with an observation o, we can reach a new belief state b'

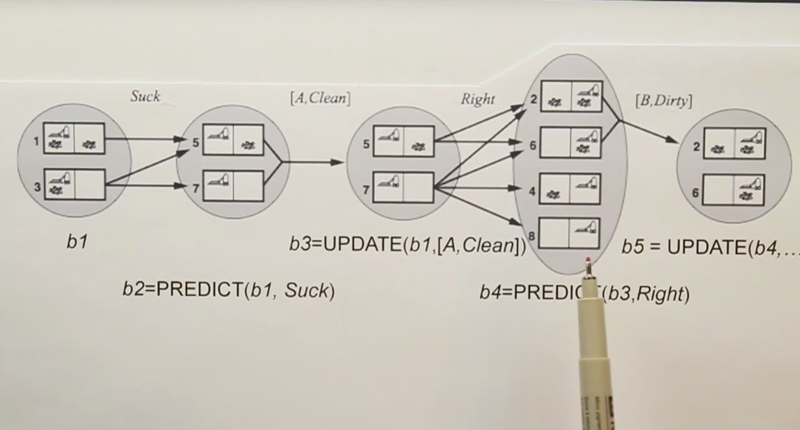
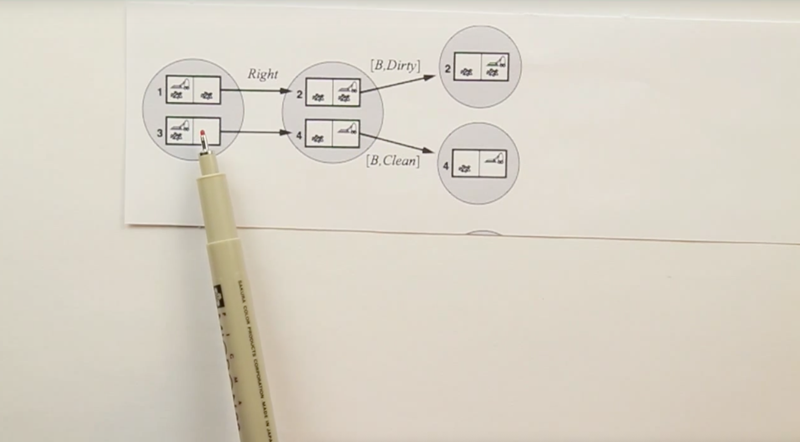
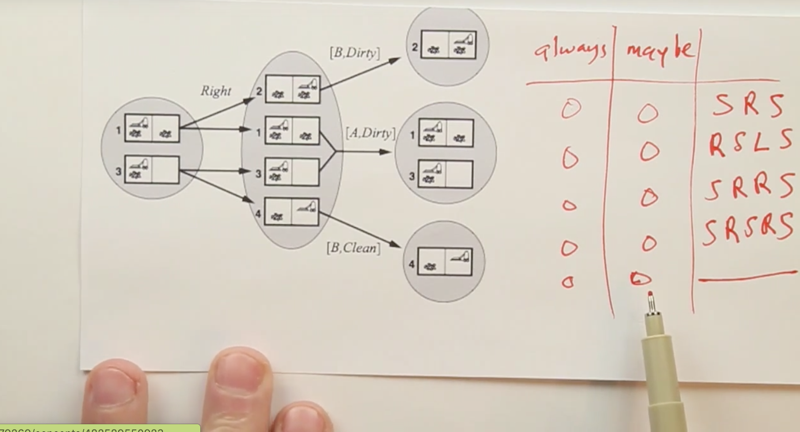
example of the mathematical notation, suck, Right are actions; [A, Clean], [B, Dirty] are observations.

Classical Planning 1

Representation of the classical planning problem with the state space, world state, belief state, and actions. An action is represented by a schema. E.g. the example above shows the action flying a plane from x to y. There is also Precondition to define all the elements and Effect of the action.

Classical Planning 2

above is an example of the initial state, goal state and action schemas of problem
the problem is to transport cargo C1 from SFO to JFK and C2 from JFK to SFO with two planes, P1 and P2.

Progression Search

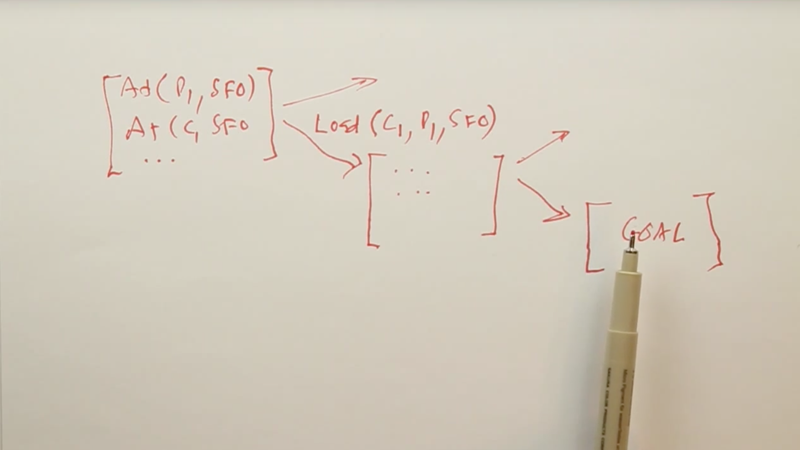
Forward or progression state space search: Just like problem solving. Start in an initial state, and then start branching on the possible actions, and continue branching out like that until we hit a state which satisfied the goal predicate.

Regression Search

In Regression Search or backward search, we can start with the goal state, search the action schema to find out what action can lead to the goal, and then search which schema can lead to that schema, then repeat until we reach the initial state.

Regression Vs Progression (an example of book buying)

a one-action world: the action is buying a book.
precondition an ISBN number of a book to buy. buy( B),
effect is own(B). if we do it in progressive search, then there are many many ISBN to buy. But if we do it regressively, the problem is much easier to solve.

Plan Space Search

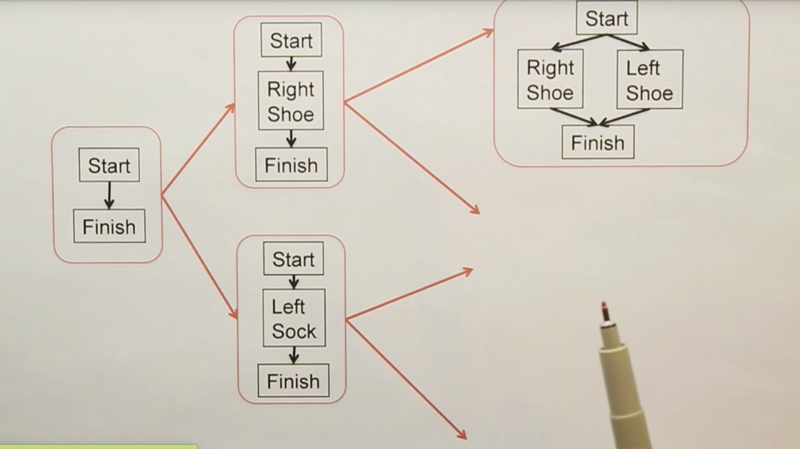
Searching through the space of plans: In a forward search, we were searching through concrete world states. In a backward search, we were searching through abstract states in which some of the variables were unspecified.

In plan space search we search through the space of plans.
- Start off with an empty plan.
- Then do an operation to edit or modify that plan by adding something in new.
- if still doesn’t solve the problem, then keep refining that plan until we got a plan that was guaranteed to work.
The most popular approaches now is forward search. The advantage of forward search seems to be that we can come up with very good heuristics for heuristic search, a

Sliding Puzzle Example

16 and 8 puzzle example

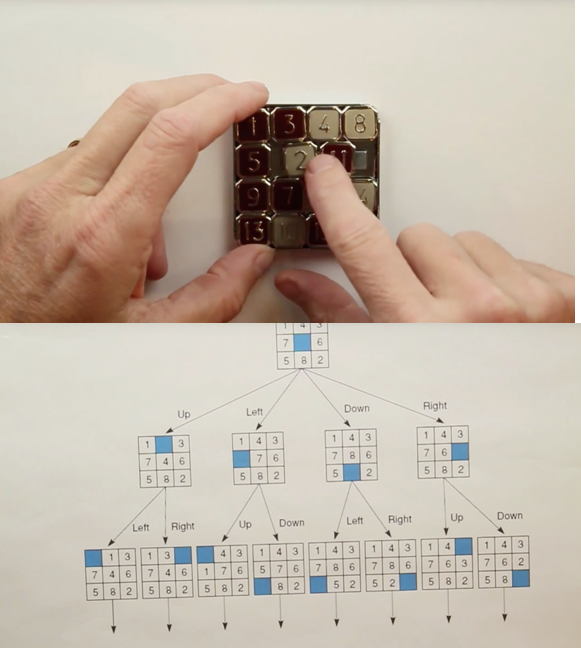
The action schema of the 8 puzzles is in the picture above.
With this kind of a formal representation, we can automatically come up with good representations of heuristics. E.g: by throwing out some of the prerequisites, we can create a relaxed version of the problem. Then we get a new heuristic.
Since the actions encoded in logical form, a program can automatically edit it and come up with heuristics without a human.

Situation Calculus 1

Another planning called situation calculus. often for FOL. It’s regular first order logic with a set of conventions for how to represent states and actions.

The conventions are shown above.
- First, actions are represented as objects. E.g. the function Fly(A, x, y) Fly A plane from Airport x To Airport y.
- Situations (also objects) correspond to the paths of actions that we have in state space search. initial situation S0, function Result(). s' = Result(s,a), here s, s' and a are all objects. Poss(a, s)

Situation Calculus 2

fluents: In situation calculus, predicates like At(p,x,s) which can vary from 1 situation to another are called fluents. They refer to a specific situation (the situation argument should be the last in the predicate).

Now, the trickiest part about situation calculus is describing what changes and what doesn’t change as a result of an action. we do 1 action for each fluent, for each predicate that can change.
successor state axioms describe what happens in the state that’s a successor of executing an action. And in general, a successor state axiom will have the form of saying for all actions and states, if it’s possible to execute action A in state S, then the fluent is true if and only if action A made it true or action A didn’t undo it.

2018-12-01 初稿

AI 笔记 Week 13 Logic & Planning