• 01 - Histograms and scatterplots
  • histograms
• 03 - Quiz What would it look like
• 04 - Histogram of daily returns
• 05 - How to plot a histogram
• 06 - Computing histogram statistics
• 07 - quiz: Compare two histograms
• 8 - Plot two histograms together
• 9 - Scatterplots
• 10 - Fitting a line to data points
• 11 - Slope does not equal correlation
• 12 - Quiz: Correlation vs slope
• 13 - Scatterplots in python
• 14 - Real world use of kurtosis

01 - Histograms and scatterplots

• One of the most informative ways to consider daily returns is when we compare the returns of one stock with another.

Time: 00:00:19

02 - A closer look at daily returns

• starting with a price time series.
• we build daily returns, this daily return data is not too revealing as time-series.

histograms

• A histogram is a kind of bar chart where we plot the number of occurrences of each item versus the value.
• split up the range of data into lots of little bins.
• and count up how many times the data matches the range across that bin.
• a bar of the appropriate height in the histogram that represents how many times the data matched that value.

Time: 00:02:12

03 - Quiz What would it look like

What the histogram of S&P 500 daily return over many years look like?

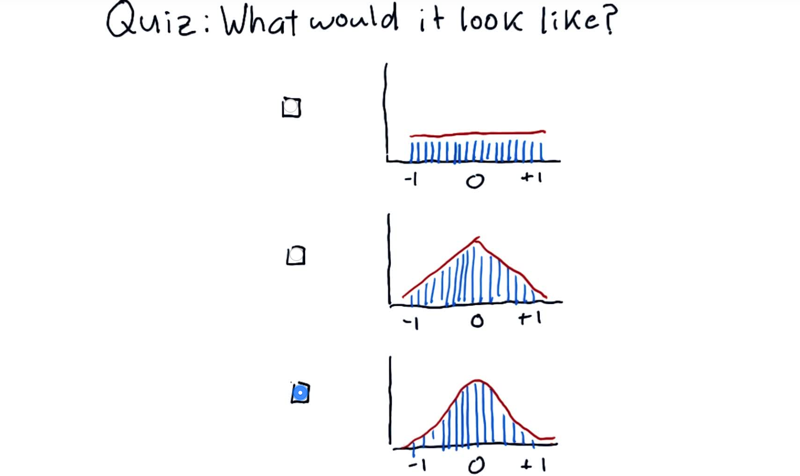
The correct answer: bell curve.

Time: 00:00:16

04 - Histogram of daily returns

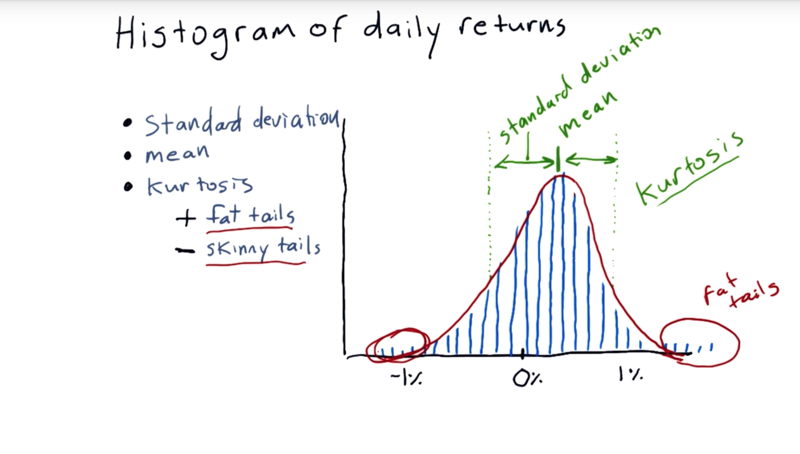
Statistics we can run on it to characterize histograms.

• mean.
• standard deviation: how far do individual measurements deviate from the mean.
• Kurtosis (means curved or arching): it tells us about the tails of the distribution. The measure of kurtosis tells us how much different our histogram from that traditional Gaussian distribution.
  • Positive Kurtosiswe indicate fat tails, Meaning that there are more occurrences out in these tails than would be expected if it were a normal distribution.
• Negative kurtosis indicates skinnytails, meaning that there are many fewer occurrences than would be expected if it were a normal distribution on the tails.

Time: 00:02:25

05 - How to plot a histogram

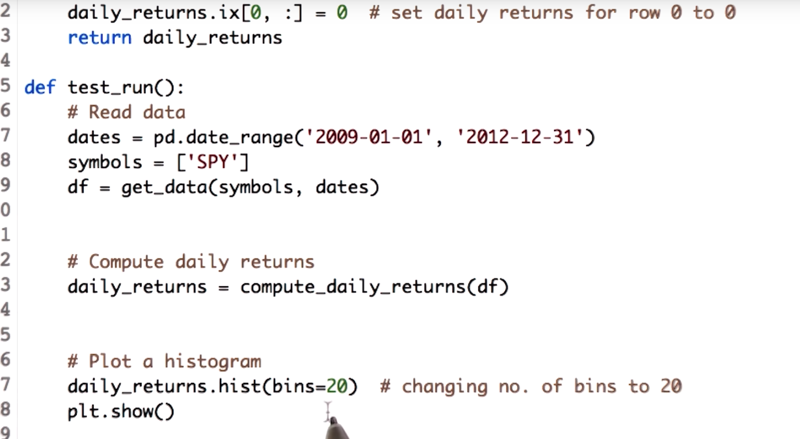
daily_returns.hist(bin=20) will plot daily_return as histogram with 20 bins. the default bin parameter is 10.

Time: 00:02:03

06 - Computing histogram statistics

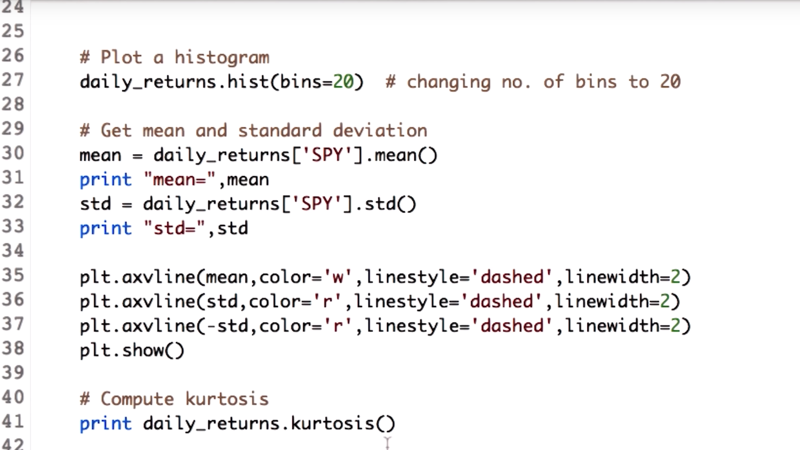Calculate mea and deviation and kurtosis:

mean = daily_returns['SPY'].mean()
std = daily_returns['SPY'].std()
kurtosis = daily_returns.kurtosis()

Plot mean and diviation using axvline() in the Matplotlib library .

plt.axvline(mean, color='w', linestyle='dashed', linewidth=2)
plt.axvline(std, color='r', linestyle='dashed', linewidth=2)
plt.axvline(-std, color='r', linestyle='dashed', linewidth=2)
plt.show()

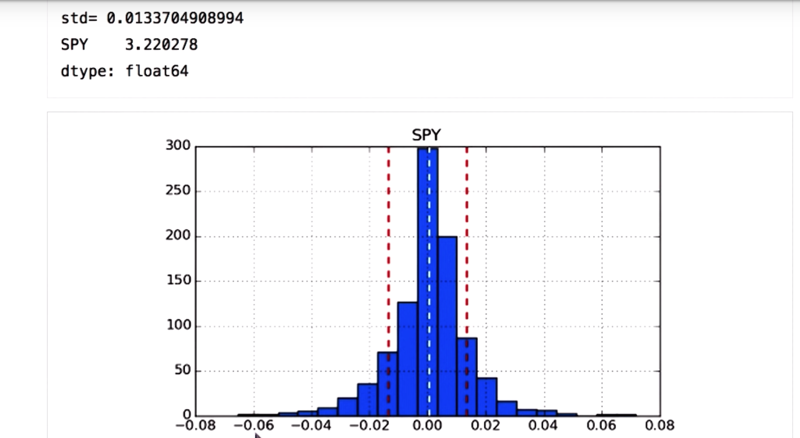
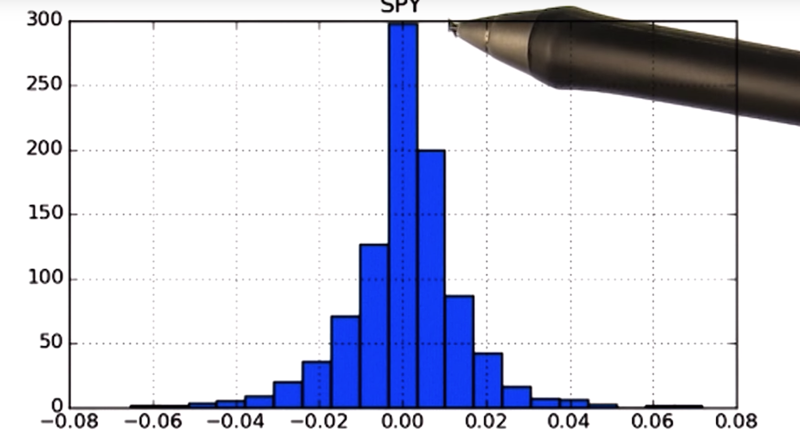
• positive kurtosis for the SPY stock, which means we have fat tails.

• Note: bincounts() using numpy.histogram function.

Time: 00:02:11

07 - quiz: Compare two histograms

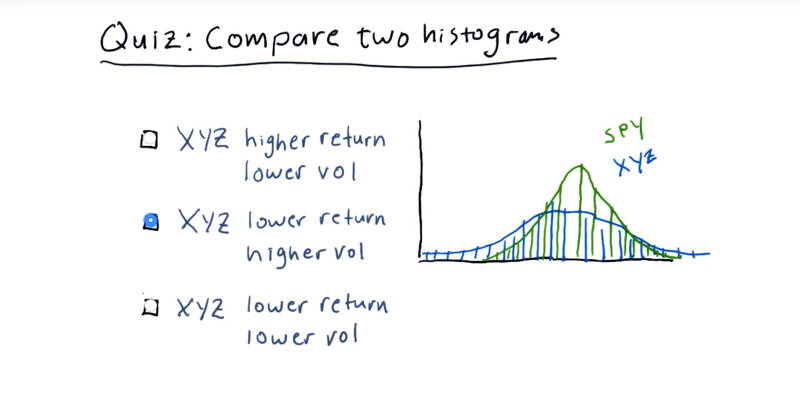
Quiz: Select the option that best describes the relationship between XYZ and SPY.

Note:

• These are histograms of daily return values, i.e. X-axis is +/- change (%), and Y-axis is the number of occurrences.
• We are considering two general properties indicated by the histogram for each stock: return and volatility (or risk).

correct answer: XYZ has a lower return and higher volatility than SPY.

• mean of XYZ, is lower than the mean of SPY.
• XYZ got a larger standard deviation (broader shoulders), therefore, higher volatility.

8 - Plot two histograms together

Since the daily_returns data frame has data for two stocks, daily_returns.hist(bin=20) will plot the data in two subplots.

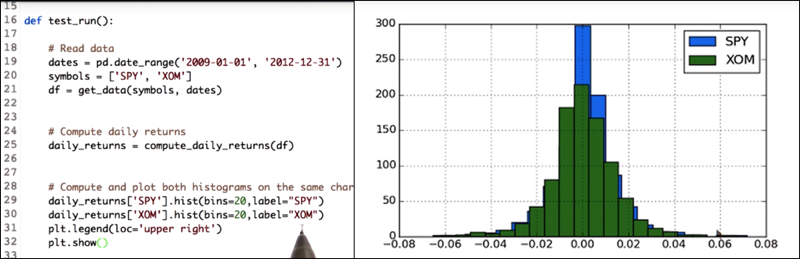
daily_returns['SPY'].hist(bin=20,label="SPY")
daily_returns['XOM'].hist(bin=20,label="XOM")
...

• To get two histograms on the same x and y axis, call the histogram functions separately on each of the stocks daily return values.
• also add the label parameter so that we can differentiate between the histogram of the SPY and XOM.

Time: 00:01:31

9 - Scatterplots

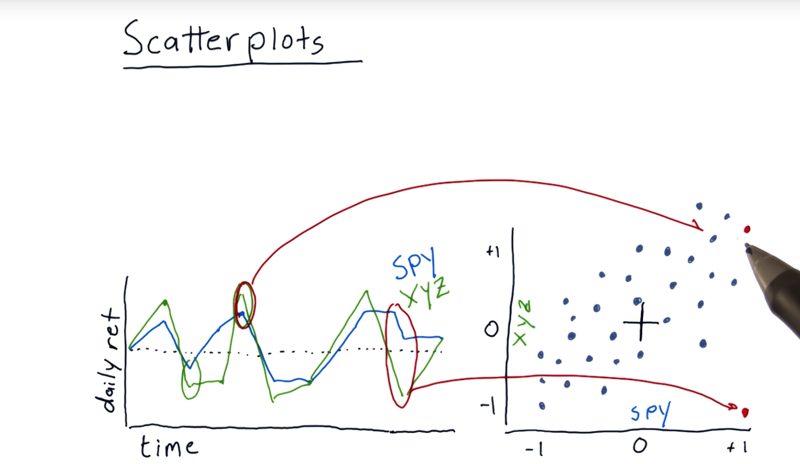
A scatterplot is another way to visualize the differences between daily returns of individual stocks. The left graph is daily return of two stocks. S&P 500 and XYZ.

• On a scatterplot, there are a number of individual points or dots represents the daily returns of two stocks that happened on a particular day.
• the dots are somewhat scattered. They don’t form a perfect line.

Time: 00:02:02

10 - Fitting a line to data points

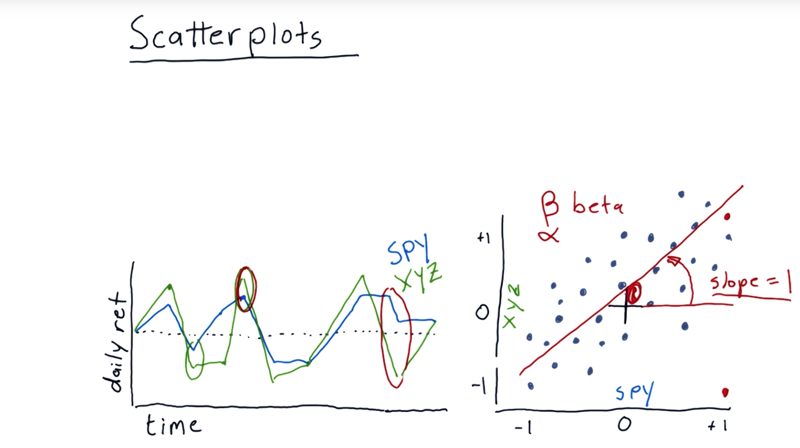
• we can fit a line to it using linear regression.
• slope, in financial terminology, is usually referred to as beta which means is how reactive is the stock to the market.
  • e.g. Beta = 1 then on average, when the market goes up 1%, that particular stock also goes up 1%.
  • if beta = 2, then if the market were to go up 1%, we’d expect on average for that stock to go up 2%.
• intercepts, also called alpha. Positive alpha means that this stock is actually on average performing a little bit better than the S&P 500 every day. If it’s negative, it means on average it’s returning a little bit less than the market overall.

Time: 00:01:53

11 - Slope does not equal correlation

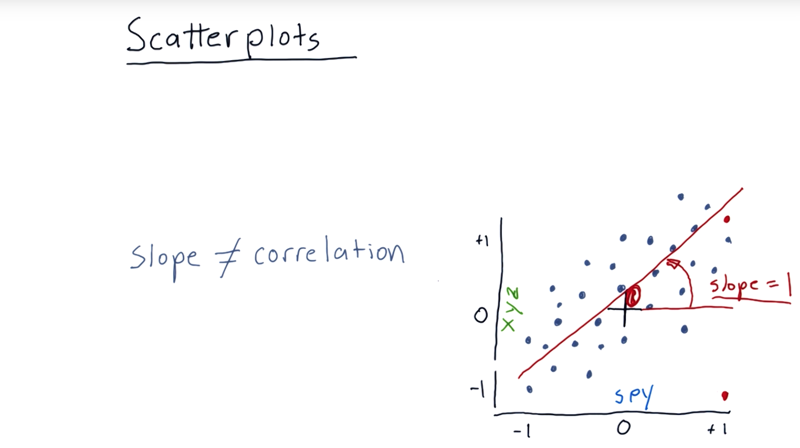
• The slope is no correlation.
• Correlation is a measure of how tightly do these individual points fit that line. the range of correlation is from 0 to 1.

Time: 00:01:15

12 - Quiz: Correlation vs slope

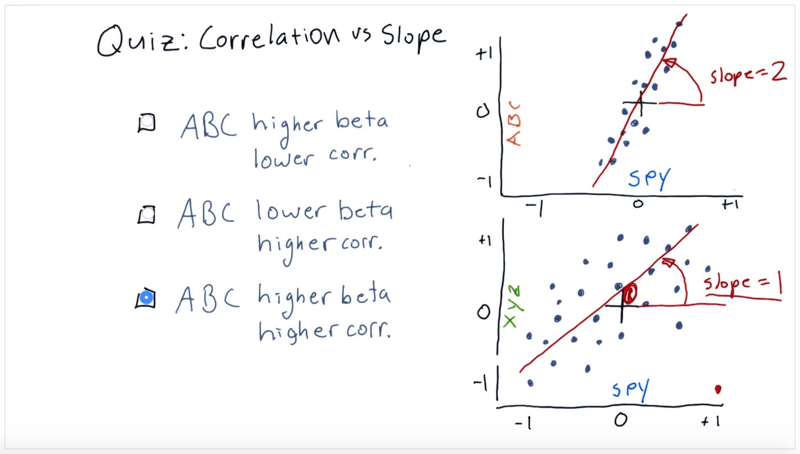
Select the option that best compares ABC against XYZ, in terms of beta (slope of linear fit) and correlation with the market (represented by SPY).

13 - Scatterplots in python

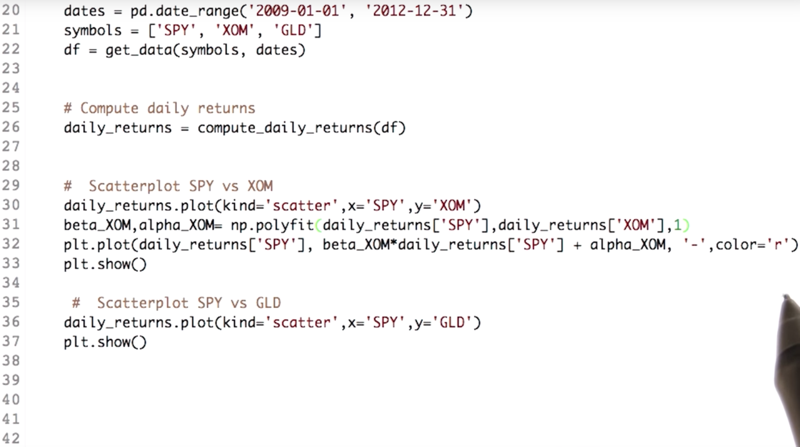Key codes

daily_returns.plot(kind='scattr',x='SPY', y='XOM') # scatterplot 
beta_XOM,alpha_XOM=np.polyfit(daily_returns['SPY'],daily_returns['XOM'], 1)
plt.plot(daily_returns['SPY'],beta_XOM*daily_returns['SPY'] + alpha_XOM, '-',color='r')
plt.show()

• Kind parameter of the plot function of the data frame will help us plot scatterplots.
• NumPy’s ployfit() function can fit a line to scatterplots and get alpha and beta of the regression line. the parameter “1” means the fitting is linear, y = mx + b.Here m is the coefficient and b is the intercept.

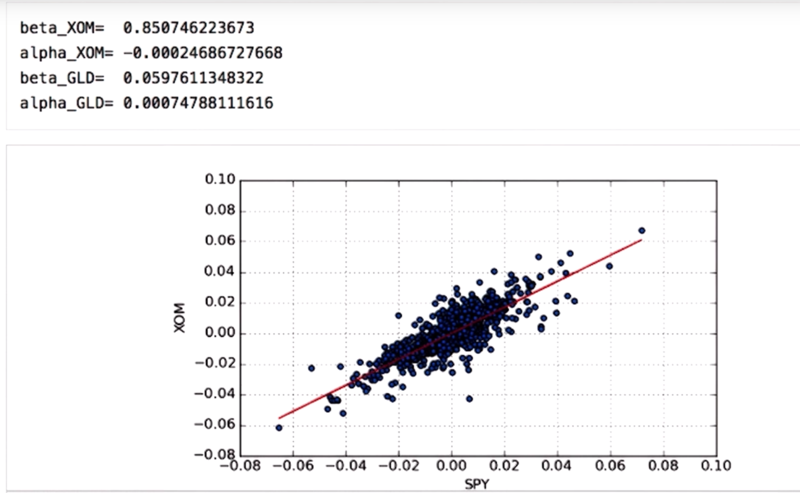
• beta values for the XOM is greater as compared to that of GLD so that XOM is more reactive to market as compared to GLD.
• the alpha values denote how well it performs with respect to SPY and Numbers indicate that GLD performed better.

One last thing is to find the correlation yet again.

daily_returns.corr(method='pearson') will output in the correlation matrix with the correlation of each column with each other column.

• high correlation means the dots fit the line closely.

Time: 00:04:45

14 - Real world use of kurtosis

• the distribution of daily returns for stocks and the market looks very similar to a Gaussian.
• but it is dangerous to assume that financial returns are normal distributions because it ignores kurtosis or the probability in the tails.
• In the early 2000s investment banks built bonds based on mortgages and assumed that the distribution of returns for these mortgages was normally distributed.
• Their model failed because of the assumption of normal distribution

Time: 00:01:06

Total Time: 00:24:11

2019-01-12 初稿