1 - What is portfolio optimization

Your final project in this mini-course is to create a portfolio optimizer.
portfolio optimization： Given a set of assets and a time period, find an allocation of funds to assets that maximize performance.
performance can be measured by a number of metrics, including cumulative return, volatility or risk, and risk-adjusted return, which is Sharpe ratio.

Time: 00:00:52

2 - The difference optimization can make

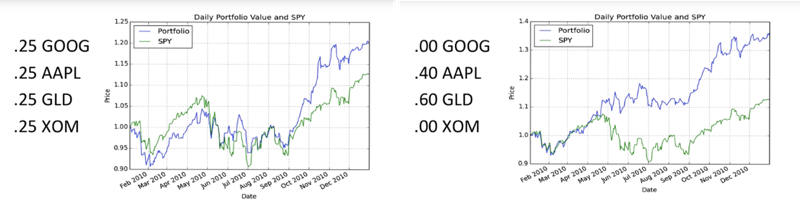
example portfolio: Google, Apple, Gold, and Exxon from the beginning of 2010 to the end of 2010.
the performance of that portfolio would look like in the blue line, if we had an equal allocation
if we optimized for sharp ratio, we will get much higher performance
this is looking back in time, so we’re looking back historically.
when we optimize for sharp ratio, hold that portfolio, rebalance, in other words re-optimize that sharp ratio and continue that month by month, we very often, most frequently see that that improves the performance of the portfolio versus just an equal allocation.

Time: 00:01:55

Take these four stocks and over a particular time period, I want you to find the optimal allocation to those four stocks. ( that maximizes cumulative return, minimizes volatility, or maximizes Sharpe ratio).
Which of these optimizers would be the easiest to write and why?

it would be easiest to write an optimizer that optimizes for cumulative return.
Because all you have to do is find the single stock that maximized return over that time period.
If optimize for minimum volatility or Sharpe ratio, you actually need to evaluate various combinations of those stocks.

Time: 00:00:29

Framing the portfolio optimization problem as a minimization problem, and then we can solve it with minimizer.

First, we have to provide a function to minimize f(x) that takes in x,
- f(x) = Sharp Ratio * -1
two, an initial guess for that x,
three, call the optimizer and let it run.
x can have multiple dimensions, so each dimension of x here is an allocation to each of the stocks. X will have dimensions the same as the number of the stock to optimize. The value for each of those dimensions is the percentage of funds to allocate to each of those stocks. And they should add up to 1.

Time: 00:02:01

One of them will help your optimization run faster.

And the other is essential for you to get the right answer.

We’ll start with the faster thing first.

First thing the ranges for each value for X is between 0 and 1. this will make the optimizer runs faster since it does not have to optimize values outside the range
Another thing you can do with the optimizers in NumPy are providing constraints. The sum of the absolute values of X must be equal to 1.0. In other words, our total allocation should add up to 100%.

Time: 00:02:16

Total Time: 00:08:01

2019-01-21 初稿