1 - Risks for hedge funds

Hedge funds seek market relative or stocks that will go up more than the market when the market goes up, and stocks will go down less than the market if the market goes down.
Hedge funds can take advantage of the CAPM to virtually guarantee a positive return.

Time: 00:00:29

2 - Two stock scenario

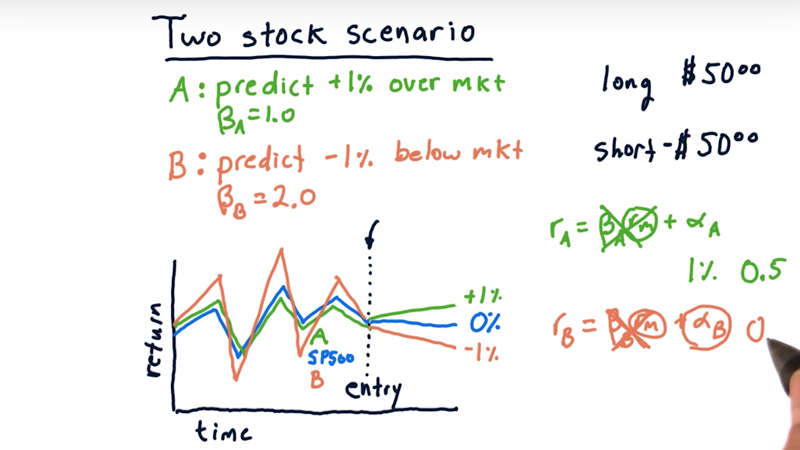
As an illustration of how hedge funds use CAPM, let’s consider a two stock scenario.

long short portfolio

our hedge fund predicts 1) stock A is going to go up 1% over the market in the next ten days. And the beta for stock A (with regard to the market) is 1.0; 2) stock B will go down 1% and the beta for stock B is 2.0.
so we’ll long stock A’s and short stock B.

first scenario: the market stays flat (returns 0%) over these following ten days, we enter our positions is a $50 long position in stock A and a $50 short position in stock B.

For Stock A the return will be $50 * 1% = $0.5
For Stock B the return will be -($50 * -1%) = $0.5
so the total return is 1% for our total investment.

Time: 00:02:59

3 - Two stock scenario quiz

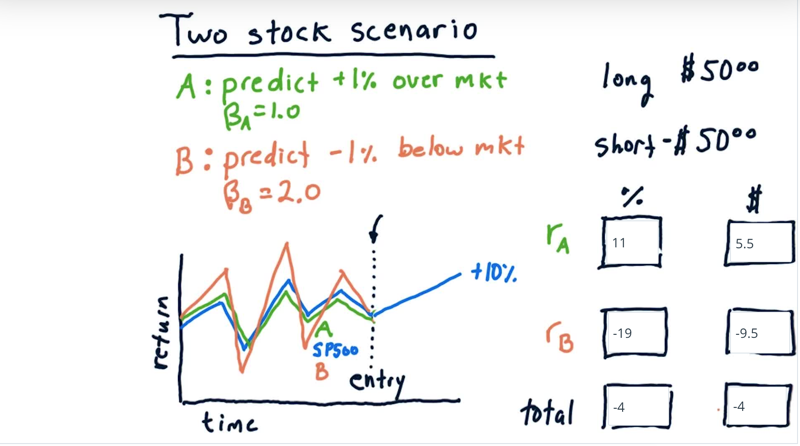
Second scenario: the market goes up 10%?

what is the expected return percentage-wise and then also in terms of dollars?

Solution:

When market one up 10%, the predicted A will be $\beta_A * r_m + 0.01 = 1 * 0.10 + 0.01 = 0.11 $. we get 11% return and 5.50 in dollar amount..
the predicted B will be $\beta_B * r_m + 0.01 =-1 *( 2 * 0.10 - 0.01) = -0.19 $. and the return is -9.5 in dollars.
The total return is - 4% and we lose 4 dollars

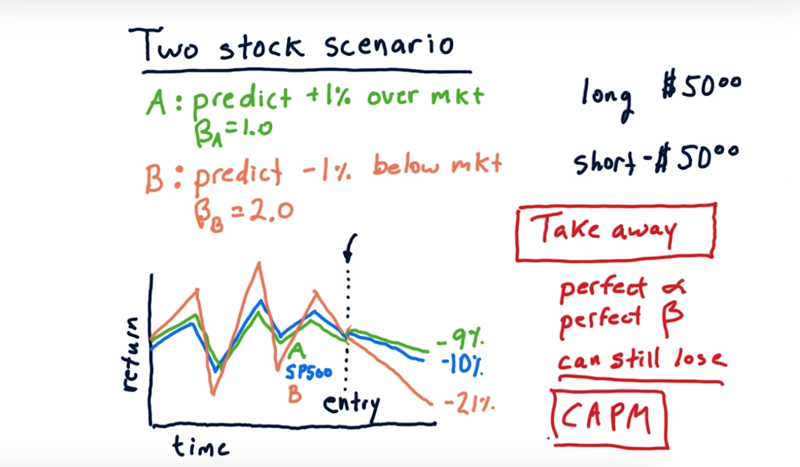
What if the market goes down 10%?

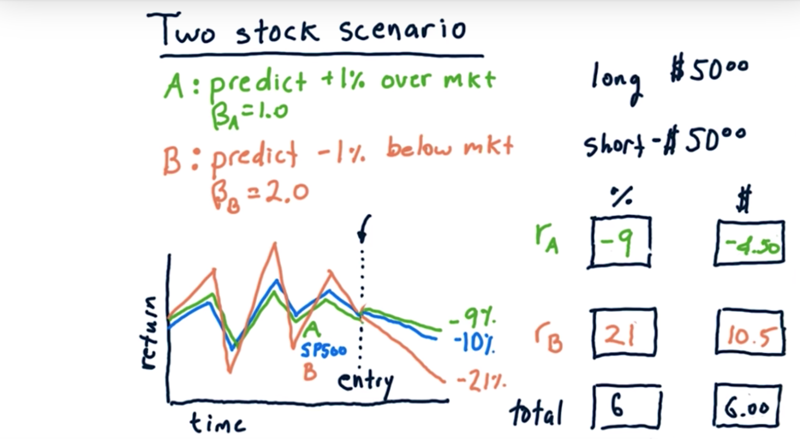
Stock A should go down 9%, Stock B is going to go down 22%. Lose money in A since we are longing it and gain money from B since we are shorting it.
altogether, we make 6 dollars.

the take away

Even if we have perfect $\alpha$ and perfect $\beta$, we can still lose if we’re not careful about how we allocate our money.

Time: 00:02:28

#4 - Two stock CAPM math

Expand the CAPM equation, we get $r_p = \sum_iw_i(\beta_i r_m + \alpha_i)$ $ =( w_A\beta_A + w_B\beta_B) r_m + w_A\alpha_A + w_B\alpha_B$

if we plug in the value of w, $\alpha,\beta$, we can get the portfolio return $r_p$
Note: $\alpha$ come from the prediction or information of our models.
$r_m$ is out of anyone’s control and is no information. we don’t have any knowledge to predict the market overall.
BUT, we can minimize market risk by minimizing the value from non-informational source. In this case, we can tweet weights to make $w_A\beta_A + w_B\beta_b = 0$.

Time: 00:02:46

5 - Quiz: Allocations remove market risk

Again, Stock A:$\beta = 1.0, \alpha = +1%$. Stock B : $\beta = 2.0, \alpha = -1%$.
long on A and short on B.

what should the weights be so that we can minimize or eliminate market risk.

Solution:

Solve the problem below: $w_A\beta_A + w_B\beta_B = 0$ and $|w_A| + |w_B| = 1$

Time: 00:01:11

6 - How does it work

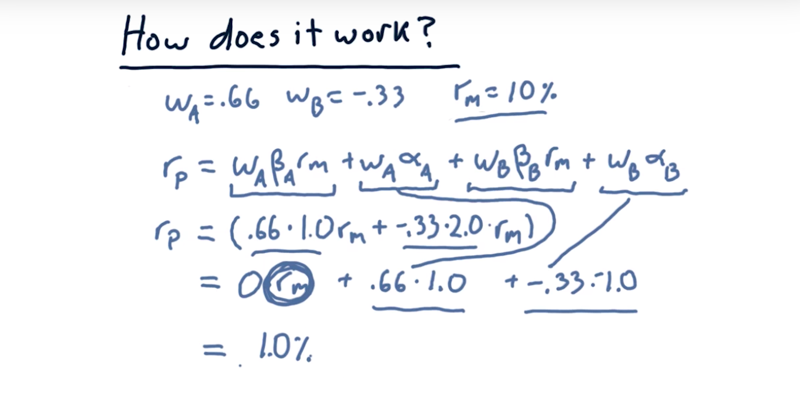
in the example above, we can do the calculation and find out, if we allocate stock A as 0.66 and stock B as -0.33, if we predicted the $\alpha$ is correct, we can always get 1% return. <– And we eliminated the return on the market.

Caveats:

$\beta_s$ aren’t fully guaranteed to continue into the future,
$\alpha_s$ aren’t guaranteed, either.
it is a way to use long/short investing to reduce exposure to the market overall and to focus on those alpha components where we do have information.

Time: 00:01:57

7 - CAPM for hedge funds summary

Assuming:

we have some sort of actionable information that we can convert into a forecast $\alpha$,
We have the $\beta$ of that stock with regard to the market.

We can:

minimize market risk by finding a $\beta$ for our portfolio that’s equal to zero finding the appropriate weights on each individual stock.
Finding the right weights is basically portfolio construction and CAMP is a great tool for that.
CAMP enables the long short trading.

Time: 00:00:55

Total Time: 00:13:37

2019-02-18 初稿

ML4T笔记 | 02-05 How hedge funds use the CAPM