- 01 - The Capital Asset Pricing Model
- 02 - Definition of a portfolio
- 03 - quiz Portfolio return
- 04 - The market portfolio
- 05 - The CAPM equation
- 06 - quiz: Compare alpha and beta
- 07 - CAPM vs active management
- 08 - CAPM for portfolios
- 9 - quiz: Implications of CAPM Quiz
- 10 - Implications of CAPM
- 11 - Arbitrage Pricing Theory
01 - The Capital Asset Pricing Model

- CAMP is one of the most significant ideas affecting finance in the last century.
- CAMP explains how the market impacts individual stock prices.
- CAMP provides a mathematical framework for hedge fund investing.
- It was developed by a number of researchers independently in the 1960s.
- William Sharpe, Harry Markowitz, and Merton Miller jointly received the Nobel Prize for this contribution in 1990.
- The CAPM led to the development of index funds and the belief that you can’t beat the market
Time: 00:00:36
02 - Definition of a portfolio

Definition: A portfolio is a weighted set of assets.
- E.g.: a portfolio that’s got three different assets in it, Apple, Google, and Oracle. 60% in Apple, 20% in Google, and 20% in Oracle.
- 60%, 20% are the weights (wi)
- $\sum abs(w_i) = 100\%$ ( leveraged portfolio is a exception).
- returns on a portfolio: $R_p(t) = \sum_{i =1}^{n}(w_i * R_i(t))$, n = number of stocks in the portfolio.
- the equation allows short porsition and the return of it is opposite to the markect change.
ime: 00:02:05
03 - quiz Portfolio return

| weight | stock | return | Position |
|---|---|---|---|
| 75% | A | 1% | Long |
| -25% | B | -2% | Short |
Given the portfolio and return of the stocks in it, calculate portfolio return
Solution: portfolio return = 75% * 1% + (-25%) * (-2%) = 1.25%
- the weight for Stock A is .75 and the return is 1%
- the weight for Stock B is negative 25% and return is 2% .
- since we shorted B and it went down, we got a positive component there, or .5.
Time: 00:00:39
04 - The market portfolio

The Market Portfolio usually referring to is an index that broadly covers a large set of stocks.
- e.g. S&P500. The S&P 500 represents the 500 largest companies that are traded
- The index changes each day according to the prices of all of its components.
The market portfolio is a combination of those stocks in a certain weighting.
- Cap Weighted: the weight of each stock in the index portfolio is usually set according to that stock’s market cap ($ w_i = number\ of\ shares_i * price_i / \sum_{j=1}^{n}(market_Cap_j)$).
Sectors
- the US we typically break the market into ten different sectors, list four of them here. E.g.: Energy, technology, manufacturing, finance and so on.
- positive and negative news can affect each of these sectors individually without necessarily affecting the others.
So it’s not unusual to break up these large markets into individual sectors.
Note: some stocks have surprisingly large weightings (e.g. Apple and Exxon each are about 5% of the S&P 500) thus have a strong effect on what happens to this index.
Time: 00:03:46
05 - The CAPM equation
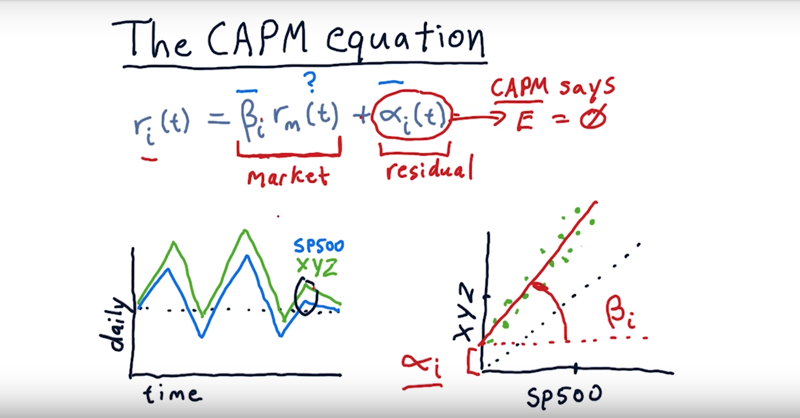
The capital assets pricing model equation.
$r_i(t) = \beta_i * r_m(t) + \alpha_i(t)$
$ r_i(t)$: The return of a particular stock, i, on a particular day, $\beta * r_m(t) $: the return for a particular stock due to the market.
- the market moving up or down strongly affects the change in price on every individual stock and $\beta$ is the extent of effects.
- every stock has it’s own $\beta$.
- $\alpha$ is called the residual which is the part that $\beta$ cannot predict.
- In the capital assets pricing model, the expectation for $\alpha$ is 0.
Where do we get this $\beta$ and this $\alpha$?
Depends on how the daily returns for a particular stock $r_i(t)$ related to the daily returns of the market $r_m(t)$.
- plot returns here for S&P 500 ($r_m(t)$.) against the daily return of an individual stock xyz ($r_i(t)$.) and fit a line to it. Then $\beta$ is the slop and $\alpha$ is the y-intercept.
- $\alpha$ and $\beta$ is based on historical data. in CAPM $\alpha$ are expect to be 0 (not always 0 in reality)
Time: 00:04:21
06 - quiz: Compare alpha and beta
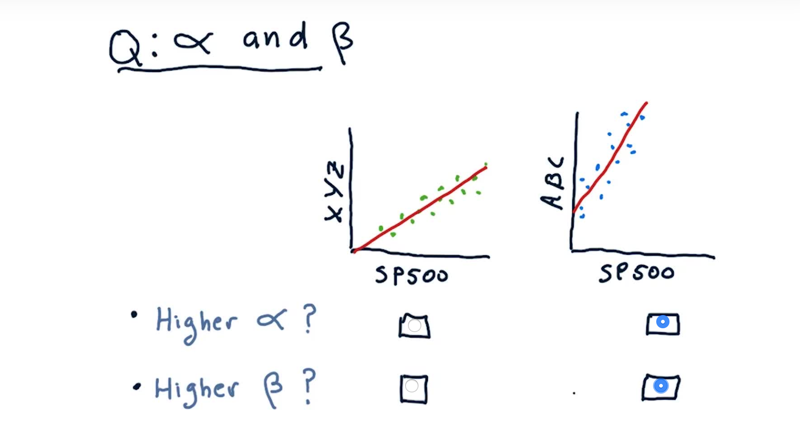
Of the two plots, which one has higher alpha and which one has a higher beta?
Solution: Correlated with SP500, ABC clearly has a greater slope than XYZ, therefore higher β. It also has a larger Y-intercept (α).
Time: 00:00:36
07 - CAPM vs active management
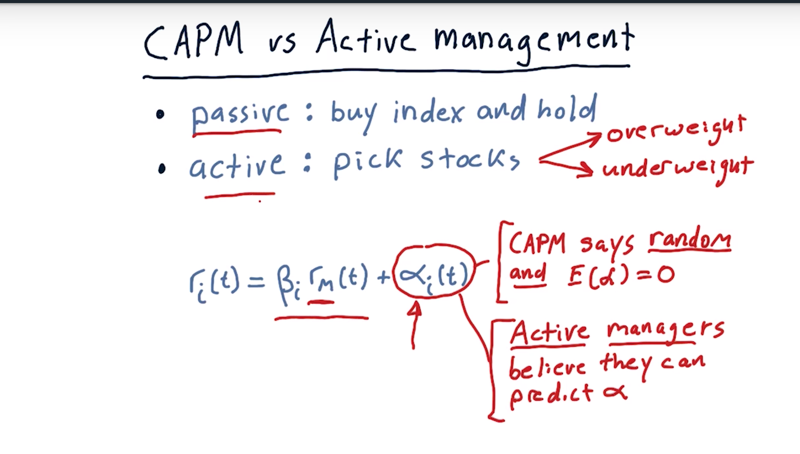
- passive investing: essentially says that you should just buy an index portfolio, hold and let it grow.
- Active investing: Active portfolio managers don’t just buy the index portfolio, they pick individual stocks. s/he weights some stocks higher and others lowers, and select higher weighted ones for his/her portfolio
consider passive versus active in that context
-
Both active managers and passive managers agree that the stock moves each day is most significantly influenced by the market $\beta * r_m(t)$.
- The CAPM the $\alpha$ is 1) random and 2) expected to be zero.
- Active managers believe they can predict $\alpha$ relative to the market.
- a passive investor believes the capital assets pricing model, Just buy an index and hold it.
- and active investor believes they or some else can find $\alpha$.
Time: 00:03:07
08 - CAPM for portfolios

the return for the entire portfolio
- compute this return for each individual stock$r_i(t)$, multiply it by the weight for that stock and then we take the sum across all the stocks.
- $r_p(t) = \sum(r_i(t) * w_i)$ (remember $r_i(t) = \beta_i * r_m(t) + \alpha_i(t))$
New way to calculate Beta
- $\beta_p = \sum(w_i(t) * \beta_i) $ and $\alpha_p = \sum(w_i(t) * \alpha_i(t))$ Thus,
- $r_p(t) = \beta_p * r_m(t) + \alpha_p$ for CAMP
- $r_p(t) = \beta_p * r_m(t) + \sum_i(w_i * alpha_i(t))$
Time: 00:02:04
9 - quiz: Implications of CAPM Quiz
Consider the implications of the CAPM, and implications in upward markets and downward markets.
If we’re in upward markets, do you want a larger beta or a smaller beta? And if we’re in downward markets, do you want a larger beta or a smaller beta?

solution: | market | stock | | ——– | —— | | Upward | larger | | Downward | smaller |
Time: 00:00:28
10 - Implications of CAPM

- $\alpha$ is random, and the expected value of alpha is zero.
- the only way we can beat the market now is by cleverly choosing $\beta$, high $\beta$ in up markets and low $\beta$ in down markets.
- the efficient markets hypothesis says you can’t predict the market which means $\beta$ is not predictable.
- taken together, CAMP and the efficient markets hypothesis say that you can’t beat the market.
Now, we are on to ways that you can potentially beat the market
Time: 00:01:31
11 - Arbitrage Pricing Theory
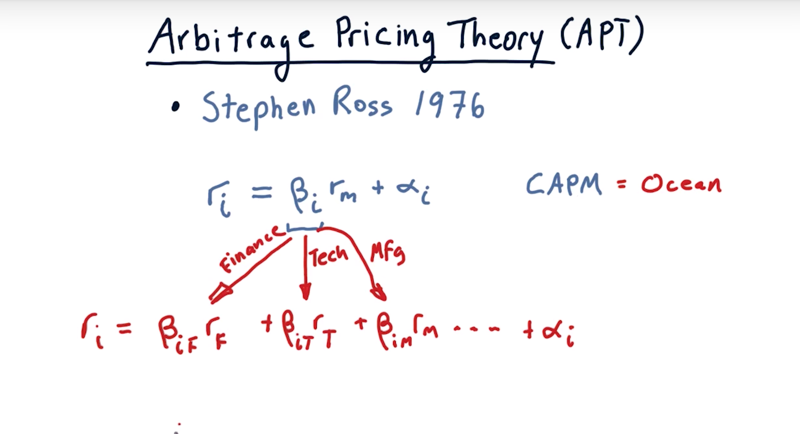
- Arbitrage Pricing Theory was developed by Stephen Ross and first published in 1976.
- Dr. Ross though using single beta that represents a particular stock’s relationship to the market is not enough; Maybe multiple $\beta s$ against different sectors.
- And of course we still have our $\alpha$.
- $r_p(t) = \beta_{iF}*r_F + \beta_{iT} * r_T + \beta_{iM} * r_M + … … + \alpha_i$
Time: 00:01:38
Total Time: 00:22:12
2019-02-18 初稿