- 01 - Overview
- 02 - Grinolds Fundamental Law
- 03 - The Coin Flipping Casino
- 04 - quiz: Which bet is better
- 05 - quiz: Coin flip casino - Reward
- 06 - Coin-Flip Casino: Risk 1
- 07 - Coin-Flip Casino Risk 2
- 08 - quiz: Coin flip casino: Reward-risk
- 09 - Coin-Flip Casino Observations
- 10 - Coin-Flip Casino Lessons
- 11 - Back to the real world
- 12 - IR, IC, and breadth
- 13 - IR, IC and breadth cont
- 14 - The Fundamental Law
- 15 - quiz: Simons vs Buffet
01 - Overview

Quotes from Warren Buffett: Wide diversification is only necessary when investors do not know what they are doing.
Mr. Buffett is talking about two things, 1) Investor skill and 2) bre,adth (the number of investments).
Time: 00:00:38
02 - Grinolds Fundamental Law

- 1980s, Richard Grinold
the Fundamental Law of Active Portfolio Management.
- performance = skill x $\sqrt{breadth}$ or $IR = IC \times \sqrt{BR}$.
- Thus Two ways to improve performance 1) improve skill, 2) more opportunities for applying that skill.
- measure of skill and some measure of breadth.
- breadth might relate to how many stocks you invest in, it is the number of trading opportunities.
- skill relates to your skill in choosing them, is summarized in Information coefficient
- performance is summarized in something called information ratio,
- information ratio refers to the Sharpe ratio of excess returns: the manner in which the portfolio manager is exceeding the market’s performance.
Time: 00:01:57
03 - The Coin Flipping Casino

A Coin Flipping is analogous to a single trade in stock: you flip a coin, you get head or tail, you buy a stock and hold it, you make or lose money.
Here, the coin is biased: we have information about this coin
- Head probability is about 0.51
- (the edge is like our alpha when investing in stocks).
- the uncertainty of the outcome is like beta in stock investing.
even money bet: bet n coins, If you win you get 2 x n coins; if you lose, your money is taken.
- There are 1,000 betting tables each with their own biased coin, and you have 1,000 tokens.
- Once you’ve distributed all your tokens, the coins are all flipped at once. Is it better to bet all your tokens on just one coin flip, or is it better to bet on multiple coin-flips at once?
04 - quiz: Which bet is better

- you put all of your 1000 tokens on a single table
- put 1 token on each of the 1000 tables,
Which one of these is better?
Solution: 2 multiple coin-flips
In 1. there’s a 49% chance you’ll lose all your money In 2, there’s very little chance you’ll lose all your money. Option 2 has a lower risk.
Time: 00:00:41
05 - quiz: Coin flip casino - Reward

Reward: expected return.
- in the context of the coin flip casino, bet 1000 chips at once. The expected return is
winning_chance x bet timesWinning change is 0.51 and losing chance is 0.49 or 49%. multiply this all out and add it up, then our expected return is0.51 x 1000 - 0.49 * 1000 = $20. - What’s our expected return in that case of betting 1000 individual chips on 1000 different tables?
Solution: still $20.
- $expectedReturn = \sum_{i =1}^{1000}expectedReturn_{table_i}=0.02*1000 = 20$
- each of the 1000 bets has 0.51 chance of winning $1, and 0.49 chance of losing $1.
- the expected return of each bet is 0.02, and we multiply it by a thousand and we get $20.
So the reword of the single betting and multiple betting is the same, so why the multi-bet approach is better?
RISK
Time: 00:00:59
06 - Coin-Flip Casino: Risk 1

Risk as the probability of lose it all: what’s the chance you might lose it all?
-
single bet: there is a 49% chance to lose all in one bet. this is very high
-
multi-bet case: the chance of losing it all $p_{loseAll} = \prod_{i=1}^{1000}p_{i} =0.49^{1000}$
- It’s so small it’s not even a number.
Time: 00:01:59
07 - Coin-Flip Casino Risk 2

Risk as the standard deviation of all those individual bets
for the multi-bet: Because for each table, the result is either -1 or 1, so that the standard deviation is easily calculated as 1.0.
- for the single bet of a 1000 tokens: we have 1) 1000 bet on one table and 0 bets on the other tables, turns out a little bit differently. the standard deviation on this event is the same 31.62.
Time: 00:02:20
08 - quiz: Coin flip casino: Reward-risk

Risk adjusted reward
- it is like the Sharp ratio that we’ve looked at in other contexts.
- single bet case: expected return was $20 and our risk was $31.62,
adjusted reward/ ratio = 0.63. - for multi-bet case: adjusted reward/ ratio =?
__Solution: adjusted reward/ ratio = reword/risk = $20/1 =20
so, A thousand bets is better than a single bet.
Time: 00:00:28
09 - Coin-Flip Casino Observations

- So bet all 1,000 chips on a single coin flip: the sharp ratio for the single $SR_{single} = 0.63$
- 1000 times in other words 1 chip on each of 1000 tables, the sharpe ratio is $SR_{multi} = 20$.
- $SR_{multi} = 20 > 40 \times SR_{single} $
- In general, $SR_{n} = \sqrt{n} SR_{single} $ wehre n = number of bets
- this relation above is exactly like the fundamental law of active portfolio management.
Performance is related to skill (how good are you at predicting the future return of the stock) and breadth (by the square root of your breadth).
Time: 00:02:34
10 - Coin-Flip Casino Lessons

-
The Coin-Flip Casino experiment enabled us to allocate our 1,000 tokens to 1,000 tables.
-
We looked at two extreme cases: 1) a small bet on all 1,000 tables, 2) all our money on one table.
-
The expected return was the same in both cases, about $20, but the risk was substantially higher for the single bet case. True for both risk to lose everything and risk as standard deviation.
Three lessons.
1) higher alpha generates a higher Sharpe ratio. (reword) 2) more execution opportunities provides a higher Sharpe ratio. (breadth) 3) Sharpe ratio grows as the square root of breadth.
Time: 00:00:53
11 - Back to the real world
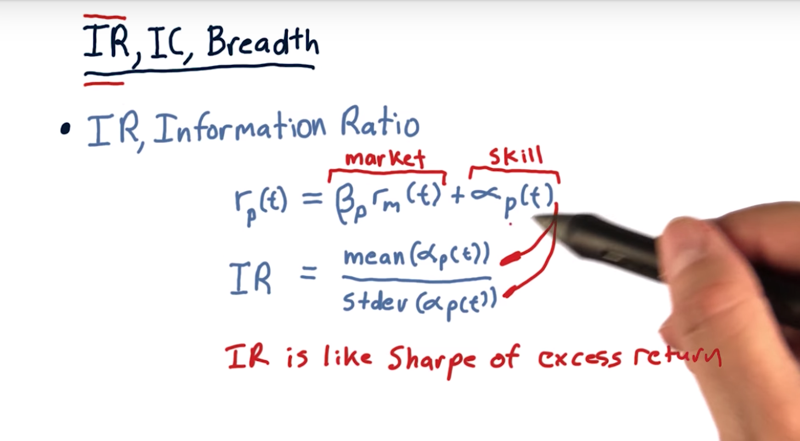
- information ratio.
- recall, $r_p =\beta \times r_m + \alpha$. portfolio return is the market component of the return $\beta$ times the market return, plus the residual return $\alpha$.
- alpha is about skill. the Sharpe ratio of this skill component is the information ratio.
- $IC = mean({\alpha}) / std( \alpha) $ Note the risk and reword are calculated by looking back historically at the daily values of alpha.
- information ration applies in many different cases, not just in this fundamental law case.
The information ratio is essentially a Sharpe ratio of excess return, this part that’s due to skill.
Time: 00:02:09
13 - IR, IC and breadth cont

- information coefficient (IC), is the correlation of the manager’s forecast to actual returns.
- breadth (BR) represents the number of trading opportunities per year.
- If hold 120 stocks all year, that’s 120 trading opportunities.
- if trade 100,000 times per day, multiply that by the trading days in a year,
- Key is if buy and hold, the number of positions in that portfolio is the number of trading opportunities.
Time: 00:01:10
14 - The Fundamental Law

the fundamental law as expressed by Richard Grinold.
IR = IC * sqrt(BR)or $IR = IC \times \sqrt{BR} = mean(\alpha) / std(\alpha) * \sqrt{BR}$
Proof of the Fundamental Law
- Since performance is related to skill and breadth of a manager, one can improve the performance by improving a skill or increasing breadth (by applying the skill to more investment opportunities).
- it is a lot easier to increase breadth by finding additional stocks, but please keep in mind, as you increase the breadth, the overall performance only increases as $\sqrt{BR}$.
Time: 00:01:39
15 - quiz: Simons vs Buffet

Assuming that both Simons and Buffet have the same information ratio and that Simons’ algorithms are only one 1000th as smart as Buffet and that Buffet trades 120 times per year.
Given that, how many trades must Simons execute in order to maintain the information ratio at the same level as Buffet?
Solution: 120,000,000
- $IR_{Buffet} = IR_{Simons} = IC_{Buffet} * \sqrt{120} = IC_{Simon} * \sqrt{TradingTime_{Simons}}$
- So, $TradingTime_{Simons} = (IC_{Buffet}/IC_{Simons} \times \sqrt{120})^2 = (1000 * \sqrt{120})^2 = 120,000,000$
Time: 00:01:10
Total Time: 00:25:45
2019-03-05 初稿