ML4T 笔记 | 03-05 Reinforcement learning

• 01 - Overview
• 02 - The RL problem
• 03 - Trading as an RL problem
• 04 - Mapping trading to RL
• 05 - Markov decision problems
• 06 - Unknown transitions and rewards
• 07 - What to optimize
• 08 - Which approach gets 1M
• 11 - Summary

01 - Overview

Shortcomings of learners that provide forecast price changes.

• it ignores some important issues, such as the certainty of the price change.
• It’s not clear when to exit the position either.

Reinforcement learners create policies that provide specific direction on which action to take.

Time: 00:00:28

02 - The RL problem

Reinforcement learning describes a problem, not a solution.

the sense, think, act cycle Robot interacts with the environment by sensing the environment, reason over what it sees and taking actions. The actions will change the environment and then the robot sense the environment again…

__In reinforcement learning, __

• the robot observes the environment to get a state (S) of it.
• the robot processes the state and decides what to do according to the policy (P)
• so the robot takes in the state s and then outputs an action (A).
• We’ll call that action (A) and it affects the environment in some way and changes it to a new state.
• T is this transition function that takes in what its previous state was and the action and moves to a new state.

how do we arrive at this Policy?

• reward (R) is associated with taking that action in that state
• the robot’s objective is, over time, to take actions that maximize this reward.
• There’s an algorithm that takes all this information over time to figure out what that policy ought to be.

Again:

• S is the state of our environment
• Robot uses its policy(p) to figure out what that action should be.
• Robot takes action, collect the reward, and affects the environment.
• Robot need to find the pi that will maximize its reward over time.

Now in terms of trading,

• Environment = the market
• actions = {buying, selling or holding}.
• state: factors (indicators) about our stocks that we might observe and know about.
• r is the return we get for making the proper trades.

Time: 00:03:56

03 - Trading as an RL problem

Consider buy, sell, holding long, Bollinger value, return from trade, daily return， are they state， action or reward?

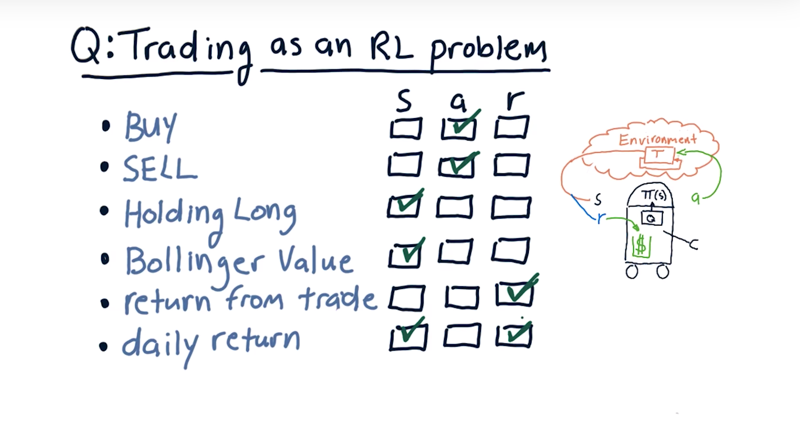
Consider each of these factors.

• Buy and sell are actions.
• Holding long is a part of the state (so is holding short)
• Bollinger value, that’s a feature, a factor that we can measure about a stock, and that’s part of the state as well.
• Return from trade, when exit a position is our reward.
• Daily return could be either a state or a reward

Time: 00:01:07

04 - Mapping trading to RL

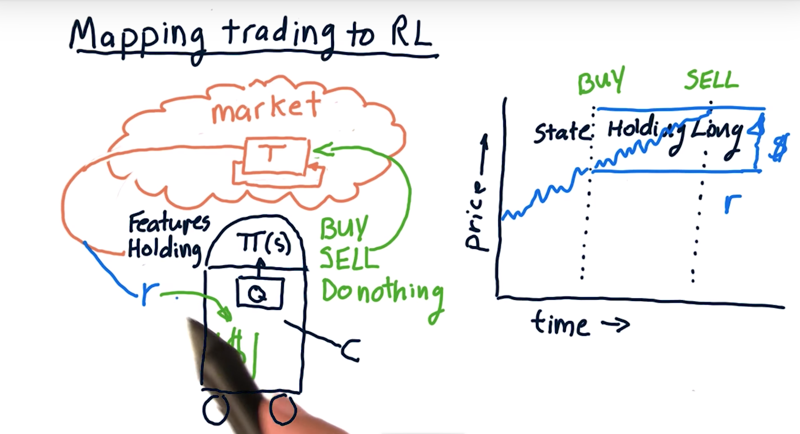
• the environment here is really the market.
• States are market features, prices, whether we’re holding the stock.
• actions: buy and sell, do nothing.

How to learn how to trade a particular stock.

• use historical time series to infer the state of the stock (Ballinger Band values, etc.)
• process that and decide what’s our action. (Suppose buy and holding long)
• Where there is a new state where the price has gone up and We’re holding long.
• new action: Sell
• Reward: The money made by the actions.

The policy tells us what to do at each state. learn the policy by looking at how we accrue money or don’t base on the actions we take in the environment.

Time: 00:01:51

05 - Markov decision problems

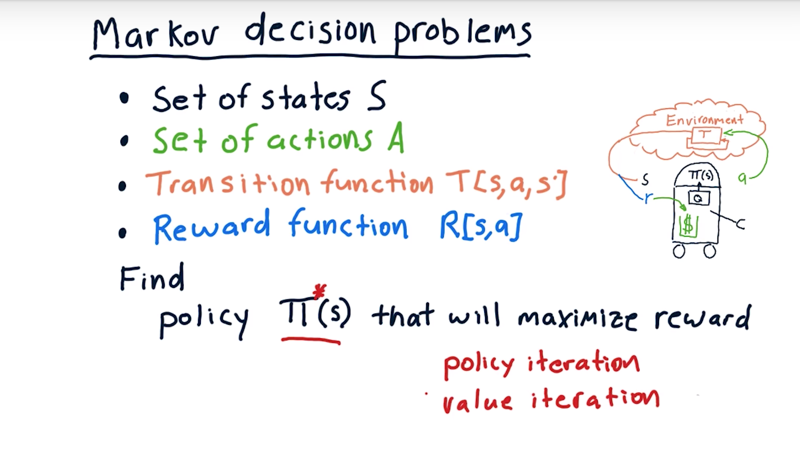
a Markov decision problem are defined by.

• a set of states S (all the possible values of S)
• a set of actions A (all the potential actions the agent can do in the environment)
• transition function T[s,a,s']: the probability of ending up in the state s' when taking action a in state s. Note: the sum of T to all the next states is 1.
• Reward function R[s,a].

__The problem for a reinforcement learning algorithm is to find this policy $\Pi$ or $\Pi^*$ that will maximize reward over time.

When T and R are known, the algorithms that will find this optimal policy are policy iteration and value iteration.

Time: 00:02:23

06 - Unknown transitions and rewards

When the transition function and the reward function are not available: The agent can interact with the world, observe what happens, and work with that data to try to build a policy.

• observe the environment, find out we are in state S1. after tooking and action, A1.then we are in S' and got reward R. - this is an experience tubal.
• Then in S2, take action A2 and in a new state S2’, and get a new reword. then repeat
• two things to do with the experience tuples to find policy $\Pi$.
  • model-based reinforcement learning.
  • model of T just by looking statistically at these transitions. Model which state we will get is we
  • Model rewards
  • When we can then use value iteration or policy iteration to solve the problem.
• model-free: Q-learning.

Time: 00:02:55

07 - What to optimize

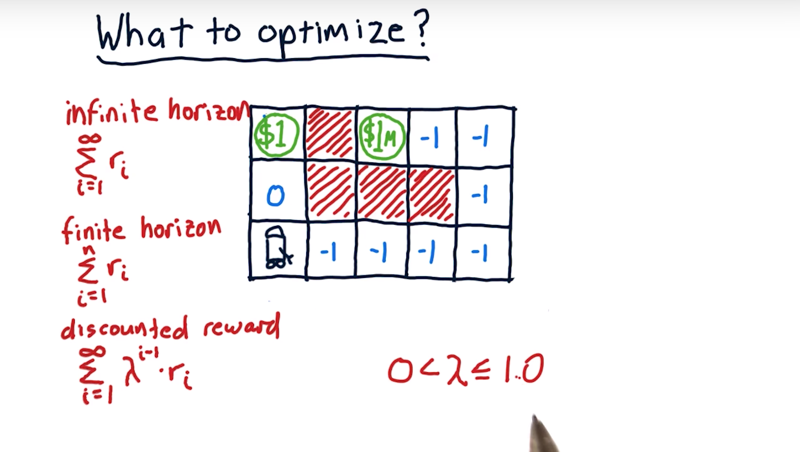
Remember, in investment, long term reward should be discounted. (e.g. $1 per day worth than $1 in the future).

The maze problem:

• Robot in the bottom left corner. $ amount in the cells are the reword. The red blocks are blocked for the robot

• We have a reward here of $1 and a reward over here of $1 million. The $1 spot will refill once the money is taken. The $1 million spot only have $1 million and will not be refilled.

• the goal is to optimize is the sum of all future rewards.

  1. if the robot can do interact with the board infinite times, it should keep moving the $1 spot. Moving to the $1 million spot won’t change the result.
  2. if want to optimize reward over three moves (finite horizon). The reward of going up is $1 and the reward of going right will be -3.
  3. if optimize reward over 8 moves, then going to the $1-million spot will be a clear choice.
  4. so, if finite moves, it makes sense to go to the $1-million spot and come back to visit $1 spot repeatedly.

Discounted reward.

• $\gamma$ is the discount factor and $\gamma \in (0, 1]$

Time: 00:06:32

08 - Which approach gets 1M

• In other words, if the robot is trying to maximize the sum over these horizons, which ones will lead it to a policy that causes it to reach that $1 million?

Time: 00:00:21 Soluiton: see the figure above.

• Infinite horizon:
  1. the robot can go to $1 and get a dollar on every other move and that will add up to infinity.
  2. It can go to the $1 million and then come back and visit the $1 spot infinity.

• Finite with n=4, no it won’t get to that $1 million.

• if n = 10, boom, it’ll reach that $1 million.
• With the discounted reward, where the dollar in the future is only worth 0.95, and it gets smaller as we get further and further into the future, but at the eight steps it will reach $1-million

Time: 00:01:11

11 - Summary

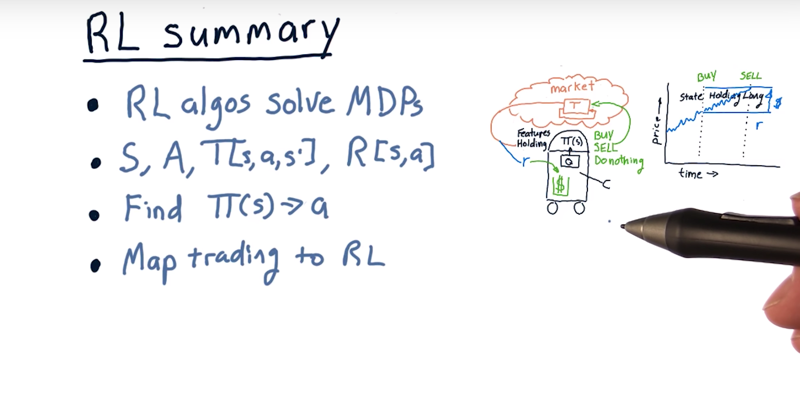
• The problem for reinforcement learning algorithms is a Markov decision problem. And reinforcement learning algorithms solve them.

• A Markov decision problem is defined by S, A, T, and R:
  • S is the potential states,
  • A are the potential actions,
  • T is a transition probability, which is given I’m in state s, I take action a, what’s the probability I’ll end up in state S’,
  • R is the reward function.
• The goal for reinforcement learning algorithm is to find a policy, $\Pi$, that maps a state to an action that we should take. $\Pi^*$ is the policy that maximizes the future sum of the reward.

=infinite horizon, fixed horizon, or discounted sum.

Map our task for trading to reinforcement learning and it works out like this.

• S, our states, are features about stocks and whether or not we’re holding a stock.
• Actions are buying, sell, or do nothing.
• The transition function here is the market,
• The reward function is how much money we get at the end of a trade.

Time: 00:01:49

Total Time: 00:23:20

2019-03-25 初稿