Machine learning 从第10周之后我就没再更新。一个原因是自己根本没时间学习,另一个原因是剩下的部分中所有内容,都是在我去年上过的另外一门课 Reinforcement Learning 中讲到了。需要那些笔记的话,直接去往下面的链接。 Reinforcement Learning 第一周课程笔记 : MDP;Reinforcement Learning 第十二周课程笔记: Game Theory I;Reinforcement Learning 第十三周课程笔记: Game Theory II & III。
下面的这部分内容是RL课中没有,而本课独有的内容。
Reinforcement Learning

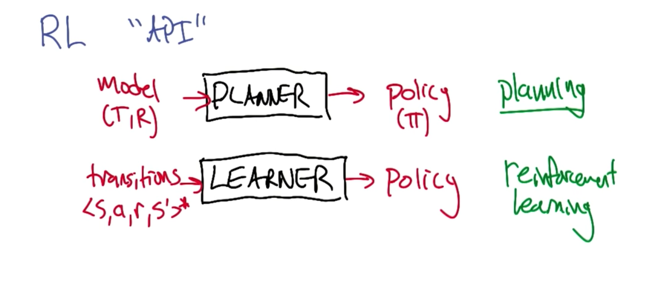
- MDP: Model -> planner -> policy
- transitions(sars) -> leaner -> policy
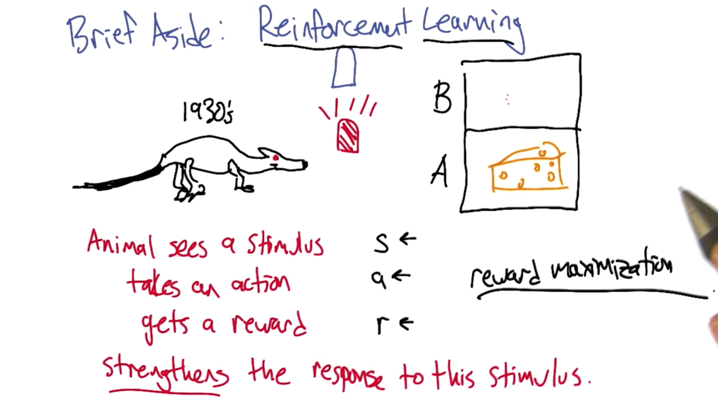
- RL = reward maximization.
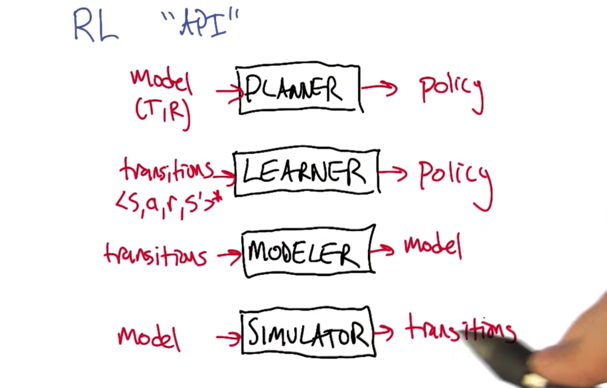
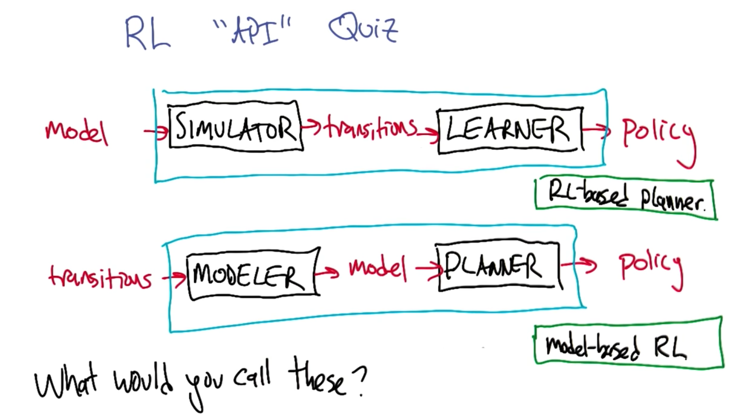
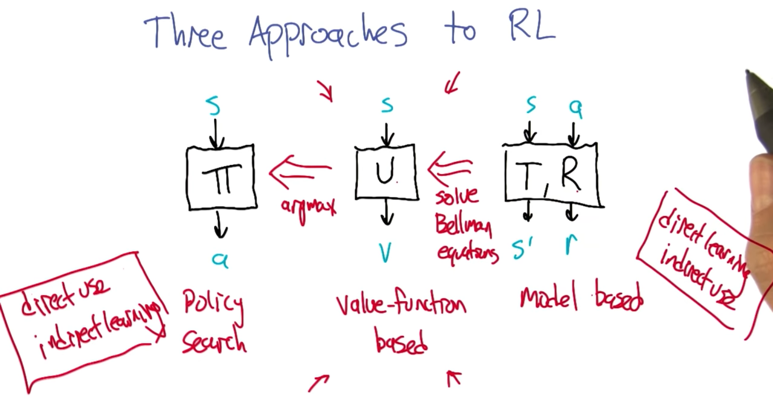
-
From Direct use/ indirect learning -> indirect learning/direct use of the policy.
- Policy search: find the optimal policy which can get the right action in given state (s).
- Value-function based: find U which can return the best value (v) for state (s). apply argmax on this will generate policy for policy search.
- Model-based approach: based on transition function and reward function, we can get the next state (s’) and reward for the current state (s) and action (a) pair. These can be used to solve the Bellman equations and eventually solve value function and given policy.

With Q, we can find out U or PI without knowing transition or action. This is why Q learning works.
Estimating Q From Transitions

- Estimated Q,(Q hat) is the utility of next state plus the current learning rate discounted by the learning rate alpha.
- V and be estimated by changing alpha

V will converge to the estimated value of X when alpha satisfies: all alphas sum to infinity, but all alpha square sum to a certain number. (e.t alpha = 1/t).
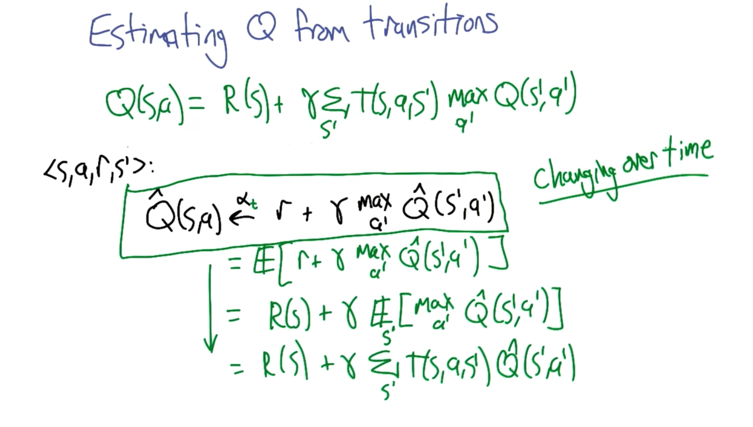
The first step is a bit ambiguous because Q-hat changes over time. But it works in practice.

Q-learning only works if s,a visited infinitely often. and alphat satisfy the conditions that it sums to infinity but the square of it sums to something less than infinity.

- always choose a0
- choose randomly
- use Q-hat
- “greedy” (local min) choose a0 if a0 is awesome
- annealing
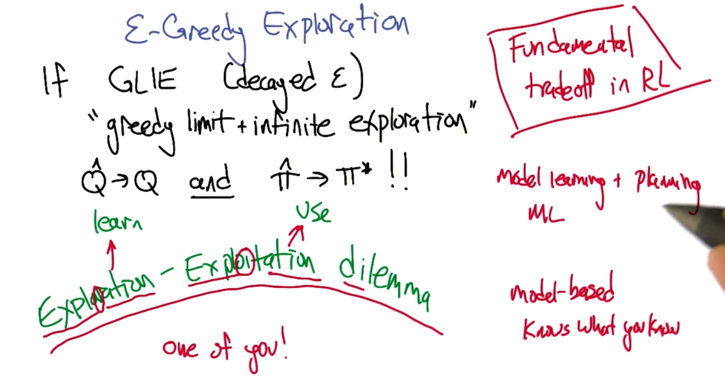
exploration & exploitation.
Wrap up
今天就要考试了,我根本就没复习好。祝我好运吧。
2016-04-30 初稿