• 01 - Overview
• 02 - Ensemble learners
• 03 - quiz: How to build an ensemble
• 04 - Bootstrap aggregating bagging
• 05 - Overfitting
• 06 - Bagging example
• 07 - Boosting
• 08 - quiz: Overfitation
• 09 - Summary

01 - Overview

• 1988, Michael Kearns and Leslie Valiant: Can a set of weak learners be combined to create a single, strong learner?

• 2006, Netflix: $1 million prize for a machine learning algorithm that could do 10% better than their own algorithm at predicting movies people like.

• 2009, The winning algorithm: a combination of several algorithm, or an ensemble learners.

Time: 00:00:42

02 - Ensemble learners

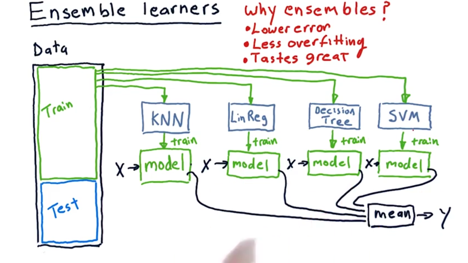
Purpose: Creating an ensemble of learners to make existing learners perform better

• assembling together several different algorithms or several different models to create an ensemble learner.
• Process: plug our data into several learners (KNN, linear regression, decision tree, etc..) and we learn several models, then query our models with an X and it get a Ys. Then get the means of the Ys as output.
• If doing classification mean of Ys does not work but we can have each of these Ys vote.
• then test this overall ensemble learner using test data that we set aside.

Why ensembles?

• ensembles often have lower error than any individual method by themselves.
• Ensemble learners offer less overfitting.

Now why is that?

• each learner has bias: e.g. with linear regression our bias is that the data is linear.
• when you put different algorithms together, you tend to reduce the biases because they’re fighting against each other’s bias

Time: 00:02:51

03 - quiz: How to build an ensemble

Given a KNN learner and a linear aggression learner, how could you go about building an ensemble?

pick the best answer.

Solution: D

A, Train several parameterized polynomials of differing degree. could work but it’s not the best answer.

B, Train several KNN models using different subsets of data. Same as above, could work but not the best.

C, Train several KNN models with randomized Y values: Wrong.

D, Combine A and B into a super ensemble. [Yes, that is the best answer.]

E, combine B and C.

Time: 00:01:01

04 - Bootstrap aggregating bagging

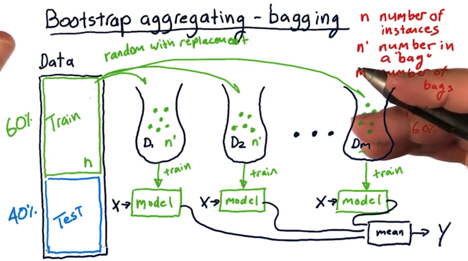
bootstrap aggregating or bagging: using the same learning algorithm but train each learner on a different set of the data.

• invented by Bremen in the late ’80s, early ’90s.

• create m number of subsets of the data from the origina data (with N members) ramdomly with replacement. each subset has a size of N’.

  • Select with replacement means at each selection, we choose from all the N cases of the data.(we might choose the same data point again)
• N is the number of training instances in our original data. N’ prime is the number of instances that we put in each bag, and m is the number of bags.

• N’ < N and usually N’ = 60% * N (rule of thumb).

• use the m collections of data to train a different model and get m different models.
• Ensamble the models: query each model with the same x and collect all of their outputs and take their mean

Time: 00:02:59

05 - Overfitting

Which of these two models do you think is more likely to overfit?

A single 1 nearest neighbor model trained on all the data or an ensemble of 10 1 nearest neighbor learners, where each one is trained on 60% of the data.

Solution: the ensemble’s going to be less likely to over fit.

Time: 00:00:10

06 - Bagging example

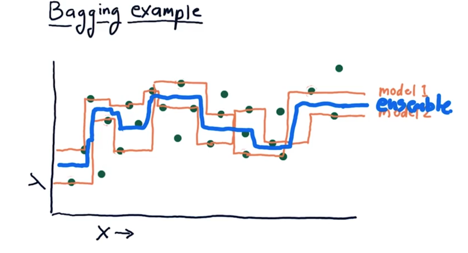
Take 1NN for example, ensemble of two 1NN leaner gives more smooth results than the two models along

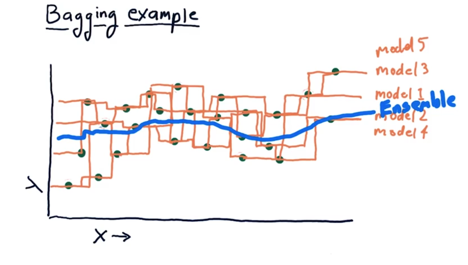
Five 1NN ensemble can give much smoother result.

Anyways, the point here is that you can build an ensemble that is much more smooth than any of the individual learners by themselves.

Time: 00:01:39

07 - Boosting

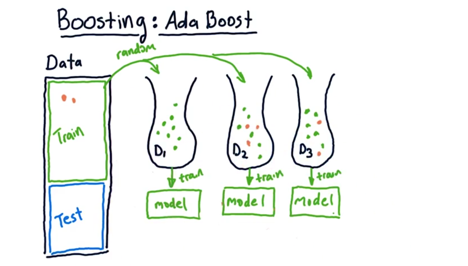
Boosting is a fairly simple variation on bagging

• Boosting aims to improve the learners by focusing on areas where the system is not performing well.

ADA boost

• build our first bag of data in the usual way (random sampling with replacement) and train a model in a usual way.

• Take all the training data and use it to test the model and discover that some of the points that are not well predicted.

• build our the bag of data by randomly from our original data but this time, each instance is weighted according to the error. (The not well predicted data points have higher chance to be selected).

• With the data, build another model and combine with the first one so we get a ensemble.

• Now test the ensemble again with the training data and measure errors. Repeat the process of weighting the data points with error, do bagging again, build another model and add it the to ensemble.

• And thus we build our next bag and our next model until m number of bags.

Difference between bagging and boosting:

• bagging: creates bags in the same way: choosing data at random with replacement.

• Boosting: choosing subsequent bags with more data instances that had been modeled poorly in the overall system before.

Time: 00:02:24

08 - quiz: Overfitation

All right, so I want you to think back over what we’ve been talking about, bagging and add a boost.

Bagging and boosting: which is more likely to overfit as _m increases?

The answer is Ada Boost.

• the reason is that Ada Boost is trying hard to match outliers and it’s striving to fit, and subsequently it may be susceptible to over fitting.

Time: 00:00:22

09 - Summary

• bagging and boosting are just methods for taking existing learners and wrapping them in this meta algorithm that converts your existing learner into an ensemble.

• An ensemble can be treated as one algorithm thus can use the same API we have been using to call an individual learner.

• The resulting learner is also likely to lower error and reduced overfitage.

• boosting and bagging are not new algorithms in and of themselves.

Time: 00:01:02

Total Time: 00:14:27

2019-01-29 初稿